
EL PROFESOR DE CIENCIAS
Número 9 - DICIEMBRE/98

Universidad Nacional de San Luis
Esta publicación está destinada a Profesores de Nivel Medio en Matemáticas y Física.
El objetivo fundamental es establecer una comunicación directa de la Facultad de Ciencias Físico Matemáticas y Naturales (UNSL) con dichos Profesores, a efectos de desarrollar actividades que permitan mejorar la calidad de su enseñanza en estas ciencias y, por lo tanto, mejorar la calidad de sus egresados.
El contenido de esta publicación estará constituido por artículos metodológicos e instrumentales para la enseñanza teórica y práctica de temas del currículum de nivel medio, problemas y su metodología de resolución, desarrollo de temas de actualidad en relación a su aplicación al currículum, prácticos de laboratorio, preguntas y respuestas para transferencia de conocimientos, noticias de carácter educativo en el área, evaluación, cartas, comentarios y artículos enviados por los docentes-lectores, donde puedan aportar, solicitar o compartir sus logros, necesidades, dudas y, finalmente todo artículo cuyo contenido los profesores soliciten, sugieran o sea oportuno incluir.
IDEA Y REALIZACION: Lic. Carlos Magallanes
TIPEO Y DIAGRAMACIÓN: María Angélica Camargo
DISEÑO EN HTML: Prof. Germán Roque Arias
Para lograr el propósito de mantener la edición de esta publicación, se necesita de la respuesta y colaboración de los destinatarios. Esto significa que es muy necesario, y se lo agradecemos desde ya, nos haga llegar sus opiniones, solicite y aplique el material que le ofrecemos, envíe artículos para publicar y difunda esta pequeña revista.
Muchas Gracias
Un problema utilizado frecuentemente en los cursos de cinemática es el siguiente:
" En un pozo de profundidad desconocido se deja caer una piedra, al cabo de n segundos se oye el golpe de aquella contra el fondo. Calculen la profundidad del pozo."
Este problema es interesante porque sirve para que el alumno aplique sus conocimientos de dos movimientos: el de la piedra en caída libre (aceleración constante ). y propagación del sonido (velocidad constante).
La solución implica la resolución de una ecuación de segundo grado en (h) (profundidad del pozo).
Se parte de la información normal:
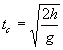 y
y ![]()
(1) 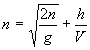 (V = velocidad
del sonido)
(V = velocidad
del sonido)
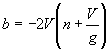
h = 70,4841 m
Hasta aquí todo correcto, pero el Profesor sabe que este resultado es falso.
El pozo es menos profundo que el valor obtenido por este camino.
La razón está en la suposición de que el aire no ofrece resistencia. Sin embargo esta resistencia existe y en algunas situaciones físicas llega a ser importante.
¿Entonces cuál es el resultado correcto?
La piedra cae en un medio gaseoso, el aire, el cual posee una viscosidad, lo que genera una resistencia que se opone al movimiento. Esta resistencia se manifiesta mediante una fuerza, que cuando la velocidad es muy baja con respecto a la del sonido, se puede expresar matemáticamente así:
![]()
Es decir se opone al vector velocidades y es proporcional a esta.
La ecuación del movimiento, en el caso ideal.
(2) ![]()
cuya solución es, como se deduce de inmediato,
(3) ![]()
La que se puede expresar así:
![]()
![]()
![]()
entonces c1 = g
(4) ![]()
Para obtener h(t) debemos integrar (3)
Se obtiene
t = 0 x= 0, resulta así que
![]()
(5) ![]()
Para resolver el problema no conviene reemplazar el h(t) dado por ecuación (5) en la (1) pues se complicaría en exceso el proceso matemático.
Recordemos la información inicial
(6) n = tc + ts
El sonido recorre la misma distancia, desde el pozo hasta la superficie, que recorrió la piedra en su caída. Por eso puedo reemplazar en (6)
(7) ![]()
Al reemplazar (5) en (7), se obtiene una ecuación que se debe resolver por método gráfico o numérico.
La ecuación a resolver es:
Para el ejemplo de n = 4 seg. propuesto al principio y con los mismos
valores de V y g, y con K=0,2 seg-1 se obtiene
Estamos de acuerdo que los alumnos no tienen los conocimientos matemáticos para analizar correctamente el problema. Pero el Profesor debe saber obtener la solución verdadera y estar preparado para dar una respuesta a un alumno de mente inquisitiva.
Es recomendable advertirle a los alumnos, que la solución encontrada despreciando la resistencia del aire entre el valor correcto y el aproximado depende de la masa del cuerpo, de su forma y de características del medio en el que cae el cuerpo.
PROBLEMAS
En el número anterior de esta revista (N° 8 pág. 37), analizamos el movimiento de un proyectil en un medio viscoso (por ejemplo aire), mediante un tratamiento vectorial de las magnitudes cinemáticas involucradas. Se supuso que la fuerza viscosa se opone en todo momento al vector velocidad y es proporcional a ésta.
Analizaremos ahora, con igual tratamiento, el caso en que la fuerza viscosa además de proporcional a la velocidad, es perpendicular a esta en todo momento.
Una situación física que, aproximadamente, satisface estas condicione en la caída gravitatoria de una hoja de papel
En la figura 1 ![]() representa
al vector velocidad y
representa
al vector velocidad y ![]() la
fuerza viscosa.
la
fuerza viscosa.
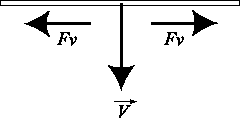
Figura 1
Indicamos con ![]() el vector
posición respecto a un sistema de referencia con versores
el vector
posición respecto a un sistema de referencia con versores ![]() y
y ![]() .
.
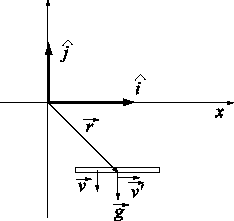
Figura 2
De acuerdo a las condiciones físicas supuestas, la fuerza resistente se puede expresar así:
![]()
donde ![]() es un vector de
igual modulo que
es un vector de
igual modulo que ![]() pero perpendiculares
entre si
pero perpendiculares
entre si
![]()
Aplicando la ley de Newton se obtiene la siguiente ecuación diferencial
(1) ![]()
por ser ![]()
reemplazando en (1), operando y separando por componentes
![]() ;
; ![]()
![]() en dirección
en dirección ![]()
No se pueden resolver independientemente una de otra.
Para resolver procedemos así:
En el sistema (2) derivamos la primera, respecto de t, y la resto m.a m. con la segunda
![]()
![]()
resulta
(3) ![]()
La (3)es una ecuación diferencial donde sólo aparece la función Vx
Para obtener una ecuación equivalente para Vy, en el sistema (2), derivo la segunda y sumo m. a m. con la primera.
Se obtiene así:
(4) ![]()
La (4) tiene la forma de la ecuación de movimiento de un oscilador
armónico, 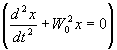 cuya solución
es de la forma
cuya solución
es de la forma
(5) ![]()
La (3) tiene una forma similar, pero es inhomogénea. En este caso la solución de la ecuación diferencial es la solución general de la homogénea más una particular de la inhomogénea.
Por observación directa se deduce que una solución particular
de (3) es ![]()
pues derivando y reemplazando esta solución en (3)
Se verifica: ![]()
Finalmente, entonces;
(6) ![]()
De (5), por integración se obtiene:
(7) ![]()
Y de (6)
(8) ![]()
Para deducir el valor de las constantes de integración aplicaremos condiciones iniciales (C.I).
Supondremos que el cuerpo parte del reposo y del origen. Es decir:
y = 0 Vy = 0
0 = A cos B B = p /2
0 = ![]() sen B + C A = -Ck
sen B + C A = -Ck
Entonces
y = -C(sen kt + p /2) + C
(9) y = -C (cos kt -1)
(10) Vy = Ck sen kt
Aplicando las C.I a (6) y (8)
0 = A’ sen B’ + C’ k
Reemplazando en (6) y (8) queda
(11) ![]()
(12) ![]()
Para encontrar el valor de la constante C, en la primera ecuación
de (2) se reemplaza Vy y ![]() a
partir de (10) y (12). El valor de C que resulta es
a
partir de (10) y (12). El valor de C que resulta es ![]()
Por lo tanto, en (9) y (10) quedan
(13) ![]()
La hipótesis inicial de que el vector velocidad y la fuerza resistente son en todo momento perpendiculares, permite inferir que esta última no realiza trabajo. Por lo tanto la energía mecánica de la hoja se conserva. Pero en la práctica esta situación es altamente improbable, por lo que en algunos puntos de la hoja no se cumplirá la mencionada situación y por lo tanto la energía mecánica de la hoja no se conserva. Esto da lugar al movimiento descendente y oscilatorio que puede observarse cuando caen una hoja de papel ó de árbol
PREGUNTAS
La enseñanza de la cinemática y dinámica rotacional es una tarea bastante difícil respecto a la situación lineal. A tal punto que prácticamente no se enseña en los cursos regulares de nivel medio.
A las características complicadas del tema, se suma la dificultad de implementar situaciones experimentales para demostraciones o verificaciones.
De este comentario surge evidente la conveniencia de construir un sistema de referencia rotatorio, para ver como se cumplen las leyes físicas estudiadas en el caso lineal. Si el alumno lograra rotar junto con el sistema, tendrá la oportunidad de "sentir" el efecto de la rotación y efectuar experimentación bajo tal situación.
El lector ya estará deduciendo que la solución exige una plataforma rotatoria sobre la que se puedan montar 2 ó 3 alumnos. Esta solución en la actual situación de las escuelas, es altamente improbable de concretar.
Sin embargo hay una alternativa que se aproxima a esta plataforma rotatoria.
Para construir esta "plataforma" rotatoria necesita cuatro (4) tablones de madera, pueden ser de aglomerado, de unos 20 mm de espesor, largo, al menos 1,50 m y ancho 50 cm.
Además un trozo cuadrado del mismo material y espesor, de 40 cm x 40 cm de lados.
Además necesitará, al menos 12 ruedas de mesa rodante,
capaces de resistir hasta 80 Kg.
La idea es armar la siguiente estructura
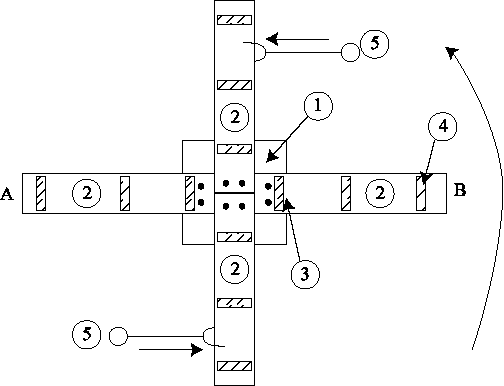
Figura 1
En la figura, (1) indica el cuadrado de madera y (2) los largueros de madera. Los extremos centrales de los cuatro largueros deben unirse a la base cuadrada, mediante tornillos ó pasante y tuerca. Conviene usar tornillo y tuerca para poder desarmar la estructura y almacenarla en poco espacio.
En la figura con (4) se indican los lugares en que deben atornillarse las bases de las ruedas pero por la parte inferior (opuesta a la cara que se ve en la figura). Las cuatro ruedas centrales deben estar a igual distancia del centro del cuadrado central. Las otras dos ruedas sobre cada larguero deben estar todas también a igual distancia del centro y ubicadas al medio y extremo de cada uno. Lo importante es que el eje de cada una de las ruedas esté alineado con rectas que pasan por el centro de la plataforma cuadrada.
Para hacer rotar la plataforma es necesario que dos alumnos la empujen a velocidad constante, (alumnos motrices).
Para empujar es necesario unir a una varilla de madera ó caño
de luz en un extremo una U hecha de alambre de construcción (diámetro
4,2 mm) ó material similar.
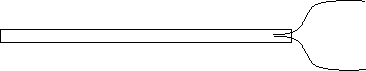
Figura 2
Se deben armar dos de estas varillas, una para cada alumno motriz. En la figura (1) se indica con (5) cada alumno empujando con la varilla.
Los alumnos experimentadores se deberán parar sobre los otros largueros, (A,B en figura (1)) cada uno cerca de un extremo exterior.
Una vez armada la plataforma y ya entrenados los alumnos motrices a empujar para lograr una velocidad angular constante, se puede empezar a efectuar distintas pruebas entre los alumnos experimentadores.
Sobre que prueba realizar queda librado a la imaginación y objetivos
que interesen al Profesor.
Por ejemplo:
El movimiento de proyectiles sobre la superficie terrestre es un tema que está presente en todos los cursos de física de nivel medio.
En el se estudian dos tipos de movimientos, uniforme y uniformemente variado. Se analizan las ecuaciones, sus gráficas, se calculan altura y alcances máximos en función del ángulo del lanzamiento.
Aquí agregaré una pregunta para el Profesor ¿Qué longitud tiene el arco de trayectoria que recorre el proyectil?
Para aquellos alumnos que tengan cálculo infinitesimal este es un buen ejercicio que une matemáticas y física.
Si consideramos un segmento elemental de trayectoria dl, e indicamos con dx y dy elementos de coordenadas, por el cálculo integral sabemos que la longitud de un arco de curva es
(1) 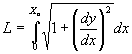
De los libros de texto, obtenemos la relación entre x e y, la cual da la función que describe la curva trayectoria
(2) ![]()
Con V0= módulo velocidad inicial y s ángulo que forma el vector V0 con el semieje x.
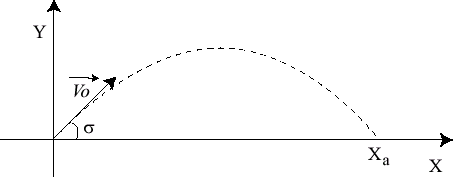
Figura 2
Luego de calcular ![]() a partir
de (2) y usando la expresión (1) obtenemos:
a partir
de (2) y usando la expresión (1) obtenemos:
(3) ![]()
Para obtener (3) se ha aplicado al caso entre X=0 y ![]() (alcance horizontal)
(alcance horizontal)
Con una computadora puede graficar (3) en función de s , y tener así una idea de la longitud del camino recorrido por el proyectil para distintos valores de V0 y s .
Para encontrar con que valor de s (para un
dado valor de V0) se obtiene L máxima se puede aplicar
la teoría de máximo y mínimo de funciones. Al hacerlo
comprobará que dicho máximo no es para s
= 45º, como es de esperar, tampoco es para s
= 90º. Para este valor de s tome límite
para ![]() :
:
![]()
Para medir la distancia focal de una lente delgada y convergente hay varios métodos.
El más utilizado es hacer incidir sobre la lente un haz de rayos paralelos entre sí y al eje principal.
Los rayos, convergen, después de refractarse, en un punto ubicado sobre el eje principal, punto al que se denomina foco. La distancia entre este punto y el centro de la lente se denomina distancia focal (f) y es una medida del poder de convergencia de la lente A menos f más convergente es la lente. Las imágenes que puedan formar las lentes convergentes pueden ser reales ó virtuales. Esto depende de la distancia (x) entre el objeto y el centro de la lente. Cuando x>f la imagen es real y cuando x<f virtual. Las imágenes reales pueden ser proyectadas y observadas sobre una pantalla. Esto es posible porque ellas son formadas por la convergencia de los rayos procedentes o reflejados en el objeto y refractados en distintos puntos de la lente. En cambio las imágenes virtuales son formadas por las prolongaciones hacia atrás de los rayos refractados.
Si se mira el objeto a través de la lente, en esta situación los rayos divergentes que recibe el ojo generan la sensación de que proceden de la imagen que está detrás de la lente.
En el caso de las lentes divergentes, la situación es complicada. Ellas no forman imágenes reales. Si se hace incidir un haz de rayos paralelos entre sí y al eje principal, después de refractarse en la lente, divergen apartándose del eje principal. Por lo tanto el método mencionado para la lente convergente aquí no se puede aplicar.
En este artículo se propone un método para que lo ensayen los Profesores y si lo consideran apropiado utilizarlo con sus alumnos.
Este método permitirá obtener un valor aproximado de la distancia focal de una lente divergente.
El método se basa en que cuando el objeto se encuentra en el foco de una lente divergente el tamaño de la imagen es mitad de la del objeto.
Veamos porqué:
La ecuación de las lentes delgadas es
![]()
Con x y x’, distancia objeto - lente e imagen - lente, respectivamente,
y f: distancia focal. En las lentes divergentes f es negativa. Si ![]()
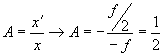
El valor ![]() indica que el
tamaño de la imagen es la mitad del que posee el objeto.
indica que el
tamaño de la imagen es la mitad del que posee el objeto.
Esta conclusión permite obtener un método sencillo para determinar f.
PROBLEMAS
RESPUESTAS
En el número anterior dejamos planteados algunos problemas para entretener a nuestros lectores.
Tal vez de ellos salgan ideas útiles para la clase.
Problema 1 (pág. 30)
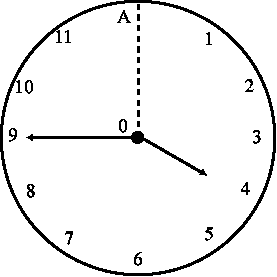 Cómo se podría
calcular el ángulo que forman el horario y el minutero de un reloj,
a una hora determinada?
Cómo se podría
calcular el ángulo que forman el horario y el minutero de un reloj,
a una hora determinada?
Por supuesto aquí no están incluidos los relojes digitales.
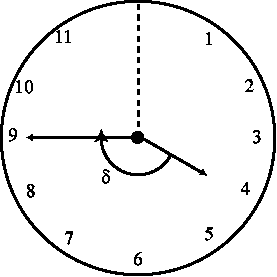
Tomemos como referencia para medir los ángulos un segmento que parte del centro de la pantalla del reloj y llega hasta 12 (ó 0)y en el sentido en que se mueven las agujas (segmento 0A en la figura)
Para determinar el ángulo entre las agujas, determinaremos por separado el que forma cada aguja con la referencia y luego por diferencia el que forman entre ellas.
Respecto al horario se observa que en cada hora esta aguja avanza 30º, valor que resulta de 360º/12 = 30º.
El minutero avanza 360º/60 = 6º cada minuto.
Por otra parte, mientras el minutero cubre los 360º en 1 hora,
el horario avanza 30º para pasar a la hora siguiente. De esto se deduce
que en cada minuto, el horario avanza 0,5º.
Ejemplo:
Horario a = 4 x 30 + 45 * 0,5 = 142,5º
Minutero b = 45 x 6 = 270º
d = b - a = 270º - 142,5º =
127,5º
 |
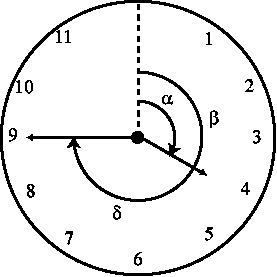 |
b = 23 * 6º = 138º
d = 281,5 - 138 = 143,5 º
Veinticinco caramelos cuestan tantos pesos como caramelos se pueden
comprar con un peso. ¿Cuanto cuesta cada caramelo?.
25 caramelos -------- x $ x caramelos ---------- 1 $
1 caramelo ----------- ![]() 1 caramelo ----------
1 caramelo ---------- ![]()
![]()
Cada caramelo cuesta 0,2 $.
Pregunta (pag 24)
¿Para qué los pájaros inflan su plumaje en los días fríos?
El aire es un mal conductor del calor. Erizando sus plumas los pájaros aumentan la cantidad de aire contenida en su plumaje. Al aumentar el espesor de la capa de aire entre las plumas se conserva más tiempo el calor generado por su cuerpo.
Pregunta (pág. 10).
En días muy fríos la nieve no apretada cruje cuando se camina sobre ella. ¿Por qué?.
En días muy fríos, en que la nieve está por debajo de 0ºC, al pisarla no se funde, como sucede cuando está a 0ºC, entonces los cristales al ser comprimidos por el peso de quien los pisa, hacen el ruido mencionado.
El carácter vectorial de algunas magnitudes físicas es importante y por lo tanto debe acentuarse tal carácter durante la enseñanza de temas que las involucren. Por ejemplo en cinemática, especialmente bidimensional, en dinámica, en las rotaciones, momento de una fuerza, etc.
La importancia mencionada hace inevitable el uso de diagramas vectoriales en la enseñanza y aplicaciones de temas donde ellas intervengan, si se pretende lograr un óptimo aprendizaje.
Por eso, en todos los buenos libros de texto, los diagramas vectoriales están presentes, tanto en el desarrollo teórico del tema como en sus aplicaciones.
El profesor sabe por su experiencia que con buenos diagramas vectoriales se le facilita la explicación de muchos temas.
Pero si la representación vectorial utilizada no es clara, seguramente generará confusión y dificultará el aprendizaje.
Las mas frecuentes dudas o confusiones en los alumnos se generan en las siguientes situaciones:
a) no darse cuenta que cuando una magnitud vectorial se descompone en componentes, estas reemplazan a aquella.
Por ejemplo las componentes de una fuerza, reemplazan a esta.
Esto significa para el profesor, la conveniencia de dibujar dos esquemas, el primero con las fuerzas con su dirección y módulo propio y el segundo donde solo aparezcan las componentes en las direcciones elegidas.
Recíprocamente, si se están representando dos o mas fuerzas que actúan sobre un mismo cuerpo y se obtiene la resultante, conviene repetir el dibujo donde aparezca solo la resultante y ya no las componentes. Esto que parece tan obvio no lo es para muchos alumnos rezagados o confundidos.
b) Confusión cuando se representan magnitudes distintas en un mismo diagrama. Por ejemplo en dinámica puede presentarse la situación de tener que representar fuerza, aceleración y velocidad en un mismo diagrama. Aquí es conveniente dibujar los vectores de la misma clase con una característica común, por ejemplo el color, el grosor de la línea, por puntos, punto y trazo, etc.
Otra opción es hacer dibujos separados, uno para cada magnitud.
c) Punto de aplicación y recta de acción.
Frecuentemente los alumnos dudan donde dibujar el vector que representa a una magnitud vectorial, especialmente con las fuerzas.
En cada situación es conveniente un análisis con el grupo para decidir donde colocar el origen del vector, por ejemplo la fuerza peso, se acostumbra dibujarla en el centro de gravedad del cuerpo, la fuerza de rozamiento en cualquier punto en la superficie de contacto de los cuerpos que interactúan.
d) Incorrecto o incompleto análisis de las fuerzas que actúan sobre un cuerpo.
Generalmente para el estudio de la cinemática y dinámica lineal de un cuerpo es necesario determinar la totalidad de las fuerzas que actúan sobre él, obtener la resultante y de ésta la aceleración para luego determinar su estado de movimiento.
Esta tarea, la de representar este conjunto de fuerzas es una fuente permanente de confusión y errores.
La primera falla que se observa es que cuando se le pide a un alumno que dibuje el vector que representa a una fuerza F que un cuerpo A ejerce sobre otro B, la dibuja en el A y no en el B. Hay una tendencia a dibujar la fuerza en el cuerpo que la genera y no en el que la recibe.
Haga pruebas con sus alumnos y asegúrese de corregir esta tendencia.
En toda situación dinámica en la que actúan fuerzas sobre un cuerpo, hay necesariamente interacciones entre dos o más de ellos. Por eso, si interesa estudiar el comportamiento de un determinado cuerpo procure simplificar los dibujos y esquemas. Dibuje únicamente el cuerpo con todas las fuerzas que sobre él actúan.
Finalmente queda hacer notar que todo lo anterior no es novedad para el profesor. Sin embargo un error común en estos es suponer que lo que está claro y obvio para ellos lo está para sus alumnos.
Sin embargo, no es así. El profesor está acostumbrado y ha madurado estos conceptos y lo que significan e informan los diagramas vectoriales. Pero para el alumno, tal vez sea la primera vez que los ve. Si no los comprende al empezar, se le generará una desalentadora confusión cuando avance en el tema.
Por todo esto, sea paciente y avance despacio al iniciar el uso de vectores. Asegúrese, alumno por alumno, que ellos están "viendo" lo que usted "ve" en los diagramas. Genere situaciones en que los alumnos deban crear ellos mismos el diagrama en lugar de copiar del pizarrón el que Ud. ha hecho. Postergue su dibujo hasta que ellos hayan intentado hacer el propio.
NOTICIA
Se informa a los lectores e interesados que el presente número de esta Revista y algunos anteriores están a su disposición en la página web de la Universidad Nacional de San Luis.
http://legba.unsl.edu.ar/~revistas/
Para consultas, sugerencias, etc., puede hacerlo por correo electrónico:
Email: cmaga@unsl.edu.ar
Facultad de Ciencias Físico, Matemáticas y Naturales
|
|
|
|
| 1 | Licenciatura en Ciencias Matemáticas |
|
| 2 | Licenciatura en Física
Título intermedio: Auxiliar en Física |
3 años |
| 3 | Licenciatura en Ciencias de la
Computación
Título intermedio: Programador Superior |
3 años |
| 4 | Profesorado de Enseñanza Media y Superior en Computación |
|
| 5 | Licenciatura en Ciencias Geológicas |
|
| 6 | Técnico Universitario en Microprocesadores |
|
| 7 | Profesorado de Enseñanza Media y Superior en Matemática. |
|
| 8 | Profesorado de Enseñanza Media y Superior en Física, Cosmografía y Física del Medio Ambiente. |
|
Requisitos de Ingreso
El aspirante a ingresar a esta Universidad, deberá presentar sin excepción y en el término de la fecha fijada para la inscripción, la documentación que a continuación se detalla:
Editor: El Profesor de Ciencias, Departamento de Física,
Univ. Nac. de San Luis. C.C. 136 – CP: 5700 – San Luis