
EL PROFESOR DE CIENCIAS

Facultad de Ciencias Físico Matemáticas y Naturales
Universidad Nacional de San Luis
Esta publicación está destinada a Profesores de Nivel Medio en Matemáticas y Física.
El objetivo fundamental es establecer una comunicación directa de la Facultad de Ciencias Físico Matemáticas y Naturales (UNSL) con dichos Profesores, a efectos de desarrollar actividades que permitan mejorar la calidad de su enseñanza en estas ciencias y, por lo tanto, mejorar la calidad de sus egresados.
El contenido de esta publicación estará constituido por artículos metodológicos e instrumentales para la enseñanza teórica y práctica de temas del currículum de nivel medio, problemas y su metodología de resolución, desarrollo de temas de actualidad en relación a su aplicación al currículum, prácticos de laboratorio, preguntas y respuestas para transferencia de conocimientos, noticias de carácter educativo en el área, evaluación, cartas, comentarios y artículos enviados por los docentes-lectores, donde puedan aportar, solicitar o compartir sus logros, necesidades, dudas y, finalmente todo artículo cuyo contenido los profesores soliciten, sugieran o sea oportuno incluir.
Publicación subsidiada por la Facultad de Ciencias Físico Matemáticas y Naturales de la Universidad Nacional de San Luis
IDEA Y REALIZACION: Lic. Carlos Magallanes
TIPEO Y DIAGRAMACIÓN: María Angélica Camargo
DISEÑO EN HTML: Prof. Germán Roque Arias
Señor Profesor:
Para lograr el propósito de mantener la edición de esta
publicación, se necesita de la respuesta y colaboración de
los destinatarios. Esto significa que es muy necesario, y se lo agradecemos
desde ya, nos haga llegar sus opiniones, solicite y aplique el material
que le ofrecemos, envíe artículos para publicar y difunda
esta pequeña revista.
Muchas Gracias
Lic. D. Perelló
Cuando se enseña interacciones entre partículas, con movimiento traslacional, se dan ejemplos de colisiones elásticas e inelásticas. El objetivo inmediato en el desarrollo de este tema es que los alumnos adquieran habilidad para resolver problemas de colisiones en distintas situaciones de velocidad y ángulo de incidencia de las partículas que interaccionarán. La solución permite predecir el comportamiento (velocidad y dirección) de las partículas después de tal interacción. Además, y como objetivo de mayor nivel conceptual está el que los alumnos comprendan la conservación del impulso lineal del sistema en ambos tipos de colisiones y la conservación de la energía mecánica solamente en las colisiones elásticas.
Cuando se estudia rotación de cuerpos rígidos no se menciona que sucede cuando ellos pueden interaccionar, pese a que es un proceso frecuente en la vida diaria. Por ejemplo una pelota que rotando es golpeada por una paleta, o un bate, un disco de embrague en un motor de automóvil, etc.
La dinámica del primer tipo de ejemplo ya fue considerada en un número anterior de esta revista (El Profesor de Ciencias Nº 7). Aquí analizaremos una colisión inelástica de dos discos que están rotando antes de la interacción.
Recuerde que en una colisión inelástica las partículas, después de la interacción, tienen la misma velocidad (lineal V en caso de traslación, y angular W en caso de rotación).
Consideremos un disco que está girando respecto a un eje central con una velocidad angular W1. Indicaremos con I1, el momento de inercia de este disco respecto al eje de rotación. Concéntrico con el anterior, otro disco está rotando respecto al mismo eje pero con velocidad W2. Indicaremos con I2 el momento de inercia de este segundo disco respecto al eje de rotación.
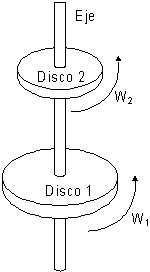 Aclaración:
Se supone que al menos uno de los discos no está rígidamente
unido al eje. Esto se hace para que puedan girar con velocidades angulares
distintas, respecto al mismo eje.
Aclaración:
Se supone que al menos uno de los discos no está rígidamente
unido al eje. Esto se hace para que puedan girar con velocidades angulares
distintas, respecto al mismo eje.
Esta es la situación antes de la interacción. Supongamos ahora que el disco 2 se desliza hasta quedar pegado al disco 1. Se produce una interacción inelástica. Ahora el sistema de los dos discos gira a una única velocidad angular, la que indicaremos con Wf.
¿Que sucede con el impulso angular L del sistema?
Antes de la interacción el disco 1 tiene un impulso angular L1 = I1W1 y una energía cinética de rotación
![]()
Análogamente, el disco 2 tiene ![]() y
y ![]() .
.
Después de la interacción, por el principio de conservación
del impulso angular, y dado que el sistema está libre de momentos
de fuerza externa, se debe cumplir que el impulso angular total se conserva.
O sea:
L1 + L2 = Lf (1)
Donde Lf es el impulso angular de la combinación final
de los dos discos pegados, o sea:
Lf = (I1 + I2) Wf (2)
Si se conoce W1, W2, I1, e I2 se puede obtener Wf.
Dado que L1, L2 y Lf tienen igual dirección, trabajaremos a partir de aquí, solamente con sus módulos.
¿Qué sucede con la energía mecánica del sistema?.
La respuesta rápida es que no se conserva porque la colisión es inelástica. Esto no basta. Corresponde demostrarlo ya que ello es sencillo.
Puesto que el sistema, por hipótesis, no se traslada, la energía cinética que posee es de rotación. Si suponemos que en todo momento la altura es la misma y que la distancia que se desplaza el disco 2 para pegarse al disco 1 es pequeña, las variaciones en energía mecánica del sistema serán de naturaleza rotacional.
Antes de la interacción la energía del sistema es:
![]() (3)
(3)
después de la interacción:
![]() (4)
(4)
Definamos:
DK = Ef - Ei (5)
Si la interacción fuera perfectamente elástica, sería Dk = 0.
Si en (1) reemplazamos L1, L2 y Lf
por sus expresiones y luego despejamos Wf, resulta:
![]() (6)
(6)
Si en (5) introducimos (3), (4) y (6) resulta:
![]() (7)
(7)
Esta expresión muestra que Dk < 0, o sea Ef < Ei. Esto significa que la energía cinética de rotación no se conserva. Algo similar a lo que ocurre en el caso lineal.
Casos particulares
![]()
Si además los discos son iguales, o se cumple que I1
= I2 = I
![]()
La energía cinética del sistema se reduce a la mitad.
c) W1 = -W2
Los discos antes de la interacción giran a igual velocidad angular,
pero en sentidos opuestos:
![]()
Si además:
I1 = I2, ![]()
Toda la energía cinética del sistema se ha transformado en otra forma de energía. Los discos después de la interacción tienen velocidad angular cero.
Por supuesto este resultado es ideal, en el sentido que es necesario
exactitud en las igualdades de los módulos de las velocidades angulares
y de los momentos de inercia, lo cual físicamente es imposible de
asegurar.
En días muy fríos, la nieve no apretada cruje cuando se camina sobre ella.
¿Por qué?
Para aplicar conservación del impulso angular en una interacción inelástica.
En los parques infantiles suele encontrarse una plataforma horizontal y circular que puede girar alrededor de un eje colocado en su centro. Tiene además soportes verticales y radiales donde los chicos se sostienen. Hace falta que uno empuje tangencialmente hasta que adquiera suficiente velocidad angular. Por supuesto que la alegría de los chicos aumenta a medida que lo hace la velocidad.
En términos de un profesor de física es necesario que
un niño, mediante una fuerza tangencial aplicada en un punto en
el borde de la plataforma, aplique un momento que genere una aceleración
angular a tal que:
r x F = I a
Donde F es la fuerza aplicada, r la distancia radial desde el eje hasta la recta de acción de F e I el momento de inercia de la plataforma mas los chicos que se encuentran sobre ella, respecto al eje central.
El problema que se propone aquí es analizar otra situación.
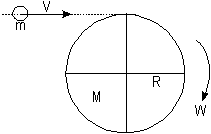
Es aquella en que estando la plataforma en reposo, viene un niño
corriendo en dirección tangencial y salta sobre ella cayendo sobre
un punto colocado en el borde de la misma. Esta situación se representa
en la figura.
Se supone que el niño salta sobre la plataforma y queda "pegado" a ella, o sea, se produce una interacción inelástica.
![]()
 ¿De
qué depende y cuanto vale la velocidad angular que adquiere el sistema
plataforma + niño?.
¿De
qué depende y cuanto vale la velocidad angular que adquiere el sistema
plataforma + niño?.
La energía cinética del sistema no se conserva. El impulso angular si.
Antes de la interacción el momento angular se debe solo al movimiento del niño.
Li = m . v . R y después de la interacción
Lf = (Ip + In) W
Siendo Ip e In los momentos de inercia de la plataforma y del niño, respectivamente, y ambos respecto al eje central de rotación.
Las direcciones de los vectores Li y Lf son paralelas al eje de rotación. Por eso trabajamos directamente con sus módulos.
Si la plataforma es homogénea ![]()
Si R es suficientemente grande podemos considerar al niño como
una masa ubicada toda a igual distancia del centro:
In = m R2
Siendo Li = Lf y reemplazando:
![]()
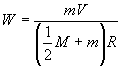
Como el coeficiente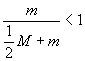 se puede
asegurar que
se puede
asegurar que
![]()
Por ejemplo si ![]() ,
, ![]()
La velocidad angular que adquiere la plataforma es proporcional a la
velocidad tangencial V con que llega el niño e inversamente proporcional
al radio de la plataforma.
Veinticinco caramelos cuestan tantos pesos como caramelos se pueden comprar con un peso.
¿Cuánto cuesta un caramelo?
La Ley de Gravitación Universal describe la atracción
mutua entre cuerpos en reposo o en movimiento relativo (para velocidades
mucho menores que la de la luz). Esta atracción es una interacción
a distancia y la forma en que esta y la masa de los cuerpos influyen en
la magnitud de tal fuerza se puede expresar matemáticamente por
la ecuación:
![]() (1)
(1)
Siendo m1 y m2 las masas gravitatorias de los cuerpos que interaccionan, r la distancia que separa sus centros de gravedad y G una constante de carácter universal, cuyo valor es: G=6,67 x 10-11 m3/Kg.s2. El signo menos indica que es una fuerza atractiva.
Si aplicamos esta ley de gravitación al caso de que una de las masas es la tierra y la otra un cuerpo en las proximidades de su superficie, la manifestación de la existencia de esta fuerza atractiva es la caída con aceleración constante de los cuerpos dejados en libertad de moverse en dirección vertical. Esta fuerza atractiva es la que denominamos peso del cuerpo y este cae siguiendo una trayectoria rectilínea que apunta al centro de la tierra.
Esta afirmación no es exacta ya que se deben tener en cuenta dos efectos de carácter local: uno es la variación de la densidad media de la tierra por la presencia de montañas o materiales de distinta densidad y en grandes cantidades y el otro efecto es que la Tierra, además de tener movimiento de traslación tiene otro de rotación. Por lo tanto, sobre los cuerpos que están cayendo hacia la tierra, actúa la fuerza de Coriolis.
Sin embargo, las correcciones que es necesario hacer son pequeñas y no modifican la esencia de lo que se quiere analizar en este artículo.
En consecuencia supondremos a la Tierra una esfera homogénea. Por lo tanto el campo gravitatorio que ella crea en su entorno tendría el mismo valor en todas las direcciones radiales y a igual distancia desde su centro.
La energía potencial gravitatoria almacenada en este campo gravitatorio
se puede deducir a partir de la relación que la vincula con el campo
de fuerzas.
![]() (2)
(2)
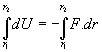 (3)
(3)
reemplazando F por (1) y resolviendo
![]() (4)
(4)
Si consideramos que r2 es un punto cualquiera y que r1
es un punto infinitamente alejado de la Tierra y que allí la energía
potencial es nula ( U(r1) = 0 ) la (4) queda:
![]() (5)
(5)
La expresión (5), en la que MT es la masa de la Tierra y m la de un cuerpo en las cercanías de su superficie, mide la energía potencial del sistema formado por ambas masas, siendo r la distancia a que se encuentra m del centro de MT y tomando como valor nulo de energía potencial cuando m se encuentra a una distancia infinita de MT.
La expresión (1) de la Ley de Gravitación Universal de Newton supone que la distancia r que separa los centros de los cuerpos que interaccionan gravitatoriamente es grande frente a las dimensiones de estos.
En el caso de un cuerpo que está en las proximidades de la superficie terrestre, la separación entre los centros de los cuerpos (r) no es grande frente al radio de la Tierra (RT).
¿Qué pasa cuando r = RT?, ¿y cuando r < RT?.
Deduciremos una expresión equivalente a (1) para la fuerza de atracción gravitatoria que valga para cualquier r.
Recuerde que campo gravitatorio se define como fuerza por unidad de masa.
Partamos de un resultado de la bibliografía que determina que el campo gravitatorio creado por una superficie esférica de paredes delgadas y en puntos exteriores a ella es el mismo que crearía si toda su masa estuviera concentrada en su centro. En los puntos interiores de la superficie esférica el campo gravitatorio es nulo.
Para el caso de una esfera maciza, imaginémosla dividida en finas capas concéntricas (como una cebolla).
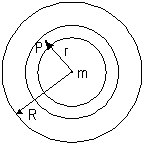 Para una capa dada y para
puntos externos a ella la masa que queda encerrada actúa gravitatoriamente
como si ella estuviera concentrada en el centro y para los puntos interiores
el campo es nulo. En la figura se muestra tal capa y en ella un punto P
cuya distancia al centro de la esfera es r.
Para una capa dada y para
puntos externos a ella la masa que queda encerrada actúa gravitatoriamente
como si ella estuviera concentrada en el centro y para los puntos interiores
el campo es nulo. En la figura se muestra tal capa y en ella un punto P
cuya distancia al centro de la esfera es r.
Por lo anterior el campo creado en P es el creado por la masa encerrada
por la capa, o sea:
![]() (6)
(6)
Si es M la masa total de la esfera, supuesta homogénea, y R su radio, la relación entre masas y volúmenes se mantiene constante para cualquier radio r medido desde el centro.
Esto significa:
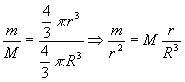
reemplazando en (6) ![]()
Si la esfera anterior fuese la tierra:
![]() (7)
(7)
cuando r = RT (cuerpo en la superficie) ![]()
Entonces (7) se puede escribir
![]() , 0 < r £
RT (8)
, 0 < r £
RT (8)
Por definición, campo gravitatorio es:
![]()
![]() , 0 < r £
RT (9)
, 0 < r £
RT (9)
la expresión (9) da la fuerza gravitatoria entre la tierra y un cuerpo que se encuentra por debajo de su superficie.
¿Qué sucede con la energía potencial U(r)?
![]()
![]() (10)
(10)
Siendo A una constante de integración a determinar. Para ello
tengamos en cuenta que la expresión (10) vale para r = RT
y que de acuerdo a (5) el valor de U(RT) es:
![]()
reemplazando en (10) y operando se obtiene:
![]()
finalmente (10) queda
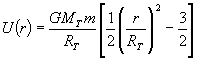 , 0 < r £
RT (11)
, 0 < r £
RT (11)
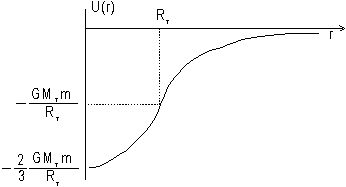 La figura muestra la gráfica
de las funciones (11) y (5) en sus respectivos rangos de validez. La (11)
para 0 < r £ RT y la (5)
para RT < r.
La figura muestra la gráfica
de las funciones (11) y (5) en sus respectivos rangos de validez. La (11)
para 0 < r £ RT y la (5)
para RT < r.
La depen-dencia de U(r) con la distancia r mostrada en la figura suele
denominarse un pozo de potencial. Esto significa que si la energía
mecánica de un cuerpo ubicado en este campo gravitatorio es negativa,
el cuerpo permanecerá dentro de este campo y no podrá escapar
de él. Es lo que le sucede a la Luna con la Tierra, a los planetas
con el Sol y a los satélites artificiales con la Tierra.
Cuando se lanza un satélite de comunicaciones, suele ser noticia en los periódicos. Si es militar o espía, se procura ignorar o disimular su lanzamiento.
En el cuerpo de la noticia se informa que tipo de actividad efectuará junto con sus características técnicas y, ocasionalmente, información sobre su órbita. En esta última parte se detalla el perigeo y el apogeo.
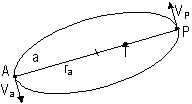 Recordemos que las órbitas
de los satélites, en su mayoría, son elípticas, estando
la tierra ubicada en uno de los focos de dicha trayectoria. Se denomina
apogeo a la mayor distancia a la tierra y perigeo a la mínima, medidas
ambas sobre el eje mayor de la elipse.
Recordemos que las órbitas
de los satélites, en su mayoría, son elípticas, estando
la tierra ubicada en uno de los focos de dicha trayectoria. Se denomina
apogeo a la mayor distancia a la tierra y perigeo a la mínima, medidas
ambas sobre el eje mayor de la elipse.
Veremos en este artículo que es posible conocer la energía mecánica (cinética + potencial gravitatoria) del satélite a partir del conocimiento de su apogeo y perigeo.
En cada uno de los puntos mencionados, la energía mecánica
E del satélite es
![]() y..
y.. ![]() (1)
(1)
Siendo M la masa de la Tierra, Va y Vp la velocidad del satélite en el apogeo y perigeo, respectivamente.
De acuerdo a la segunda Ley de Kepler se cumple
Va ra = Vp rp , en general v . r = c (constante) (2)
Aquí r es la distancia medida desde la tierra hasta cualquier punto de la órbita. Por supuesto v es la que posee el satélite en dicho punto.
Para cualquier punto la ecuación (1) se puede escribir:
![]() (3)
(3)
de (2) ![]()
reemplazando (2) en (3) y reordenando queda:
![]() (4)
(4)
esta ecuación no la puedo resolver hasta conocer E y c.
La ecuación (4) es una ecuación de segundo grado en r, sus raíces son:
![]()
![]() ,
, ![]()
Si sumo miembro a miembro
![]() , con r1 + r2
= 2a (semieje mayor de la elipse)
, con r1 + r2
= 2a (semieje mayor de la elipse)
pero r1 + r2 = rp + ra si
el valor de c incluye la velocidad en dichos puntos.
Por lo tanto:
![]()
La energía es negativa indicando que el movimiento está
controlado por el campo gravitatorio terrestre. También se puede
observar que para una dada energía mecánica del satélite,
éste puede orbitar en cualquier órbita elíptica que
tengan todas el mismo semieje mayor: rp + ra.
¿Para qué los pájaros "inflan" su plumaje en
los días muy fríos?
para el estudio de funciones
Prof. N. B. Wilches
A fines de 1995, en el Colegio Nacional "Dr. Arturo U. Illia", dependiente de la Universidad Nacional de Mar del Plata, tuvieron lugar los Concursos Docentes en el marco de un nuevo Proyecto para el Colegio.
Un grupo de docentes de distintas disciplinas fuimos designados en el Área de investigación educativa de acuerdo con las distintas propuestas que aprobaron los Jurados respectivos.
Este trabajo que presento, con el simple propósito de compartir la experiencia pedagógica que estoy implementando se encuadra en mi Proyecto de investigación pedagógica en la acción: "Un cambio de enfoque en la enseñanza de la Matemática".
No es un taller destinado a alumnos con gran gusto o predisposición hacia la Matemática, sino a "todos" los alumnos que cursan el cuarto año, durante el transcurso de un ciclo lectivo.
La problemática que planteo no está concebida como una oportunidad para que los alumnos apliquen lo que ya aprendieron a través de un clase expositiva, porque en este caso, los problemas (entendiendo por problemas a todo lo que signifique una situación nueva a resolver) cumplirían un función de evaluación y control del aprendizaje, sino que, a través de la misma, pueda gestarse un concepto matemático.
El objetivo final del trabajo es la articulación entre enseñanza
media y Universidad para que el alumno pueda elaborar y "experimentar"
los conceptos relacionados con funciones, que luego en la Universidad podrá
formalizar en el Cálculo infinitesimal.
Como Profesora Adjunta en las Cátedras de Análisis I y Análisis II observo una brecha entre el enfoque que suele darse a los temas a nivel medio y el que en forma inmediata se le da a los mismos en cualquier texto o Cátedra de Análisis en las distintas facultades.
Este trabajo pretende achicar esa brecha.
A mi criterio una herramienta muy útil para tal fin es el uso de un software especifico para graficar y obtener información sobre las distintas funciones.
La propuesta didáctica incluye un trabajo en paralelo en el aula tradicional y en la sala de Informática.
La disponibilidad horaria es de cuatro horas semanales.
Los alumnos desarrollan Guías de estudio, teórico prácticas, a las que deben dar respuesta, en un ir y venir, desde el enfoque analítico y la interpretación de la gráfica de la función que responde al modelo del problema.
Se trata en todo momento de respetar los tiempos y las inquietudes individuales de los alumnos.
Estos trabajan con el software "Funciones para Windows 2.0", Jordi Pagares Roset -1993- B. Santiago Sobrequés. Girona, y con un procesador de textos al cual trasladan las gráficas representadas en aquél.
Es un software en el entorno de Windows, al cual los alumnos están familiarizados, de uso muy sencillo, que les permite graficar cualquier función introducida en él.
Pueden modificar el valor de las unidades de los ejes, así como también los intervalos considerados en los mismos y cambiar los parámetros de las funciones.
Cuenta con Comandos que brindan información (entre otras) sobre la imagen en un punto, antiimagen, raíces, discontinuidades, puntos máximos, puntos mínimos, de inflexión, intervalos de crecimiento y decrecimiento.
La información que brindan los Comandos la utilizo para confirmar y/o rechazar las propuestas que tienen que elaborar previamente los alumnos con el estudio analítico y no como una respuesta mecánica.
En la enseñanza tradicional, al no contar el alumno con conceptos de Análisis Superior, se suele trabajar con expresiones algebraicas, que sólo exigen una aplicación rutinaria de procedimientos, o bien se le pide al alumno que efectúe un estudio muy limitado de la función asociada. Con el uso del software para graficar, el alumno puede determinar la expresión funcional que cumpla con ciertas condiciones y verificar luego visualmente si ésta responde al problema.
Durante el transcurso del año se estudian los temas: Funciones polinómicas de grado n, Funciones racionales, Función cuadrática, Función exponencial y logarítmica, en todos los casos con las ecuaciones asociadas.
Breve síntesis de las ventajas del uso del software
En funciones polinómicas
El alumno está en condiciones de:
Los profesores a cargo de los cuartos años hemos vivido en clase el desconcierto que experimentan los alumnos cuando "intentan unir los puntos" que obtuvieron mediante una tabla de valores.
Con esta metodología de trabajo están en condiciones de:
¿Cómo se podría calcular el ángulo que
forman el horario y el minutero de un reloj, a una hora determinada?
Coeficiente cinético de fricción
Esta sugerencia experimental tiene el objeto de ofrecer al Profesor de Física una oportunidad de hacer medir fácilmente a sus alumnos el coeficiente de fricción cinético.
El material necesario es una superficie firme, horizontal y lisa, por ejemplo una mesa cubierta por fórmica, vidrio o material similar. Además un cuerpo con una superficie también pulida, por ejemplo un disco de madera de unos 15 a 20 cm de diámetro y de 2 a 3 cm de espesor.
El experimento es muy sencillo. Consiste en: a) Colocar el disco sobre la mesa. Marcar alguna referencia para fijar su posición inicial. b) Con una varilla similar a un taco de billar darle al disco un golpe, tal que adquiera un impulso inicial, se deslice sobre la mesa y se detenga, sin caer de ésta, a una cierta distancia. c) El golpe del taco debe ser central, tal que el disco o cuerpo que se use, al deslizar, no gire. d) Se debe medir el desplazamiento que efectúa el disco y el tiempo que tarda en realizarlo. (Ver figura)
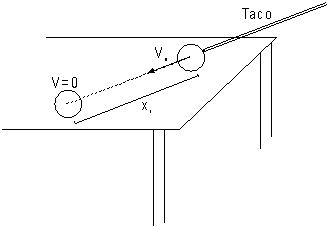 El análisis que sigue
se basa en las siguientes condiciones:
El análisis que sigue
se basa en las siguientes condiciones:
![]() (1)
(1)
![]() (2)
(2)
Para el caso que estamos considerando, el disco parte con una velocidad
inicial V0 y se detiene al tiempo tf, en tal instante
V=0. Si indico con d el desplazamiento total, de (1) obtengo ![]() , y reemplazando en (2):
, y reemplazando en (2):
![]() (3)
(3)
De la ecuación (3) se deduce que si mido d y tf puedo obtener la aceleración a, supuesta constante, con que la fuerza de fricción está frenando al disco.
Conocida la aceleración a, igualando las expresiones dadas
por la Ley de Newton y la de fuerza de fricción:
![]() (4)
(4)
La expresión (4) permite calcular el coeficiente de fricción cinético m entre la masa y el disco.
Operacionalmente se sugiere lo siguiente:
Observe que la ecuación (3) no depende de V0, por lo tanto distintos alumnos pueden hacer los lanzamientos y, por supuesto, mientras más puntos experimentales se obtengan, más fácil será obtener la recta en la gráfica.
Como extensión, si el Profesor desea puede modificar la masa del disco y ver que sucede.
Si dispone de tiempo, y le interesa, puede extender el experimento repitiéndolo con la mesa inclinada un cierto ángulo q , e impulsar el disco hacia la parte elevada de la mesa.
En esta situación m.aq =m .mg cosq .
Si obtiene aq , lo puede utilizar junto con el a obtenido anteriormente, para establecer una relación entre ellas, la cual está vinculada con q . De la comparación entre el q calculado y el q medido obtendrá una idea de la calidad del experimento realizado.
Queda para Ud. la tarea de encontrar la relación entre aq
, a y q . Es muy fácil.
Ingravidez
Imaginemos un ascensor detenido en el décimo piso de un edificio. En el piso del mismo una balanza de baño y sobre ella uno de sus alumnos. La balanza, por supuesto, marcará el peso del mismo. Si ahora, el ascensor, la balanza y el alumno caen libremente por el hueco del ascensor, y mientras va cayendo, el alumno podrá comprobar que la balanza marca cero en su escala. Esto no significa que el alumno haya "perdido" su peso. Sigue pesando lo mismo. Lo que sucede es que el ascensor, la balanza y el alumno están cayendo con la misma aceleración. Esta es la famosa ingravidez que observamos en la televisión cuando nos envían imágenes desde las cápsulas con tripulantes que orbitan la tierra.
Cuando Ud. explica esto a sus alumnos, es difícil eliminar la asociación entre ingravidez y ausencia de peso, y por supuesto, le resulta difícil, tal vez imposible, demostrarlo.
Esta sugerencia experimental pretende ayudarle un poco con la esperanza de que la pueda aprovechar y convencer a sus alumnos.
Necesita un envase de plástico transparente de unos dos litros, como el de las conocidas gaseosas o similar. Cerca del fondo y en costados opuestos haga dos agujeros enfrentados de uno o dos cm. de diámetro. Con sus dedos pulgar e índice tape ambos agujeros. Llene el envase con agua.
Si sostiene el envase con la otra mano y por su parte superior, al retirar los dedos el agua empezará a caer por la acción de la gravedad.
Ahora, y sobre un lugar con el piso seco, sostenga el envase frente a sus ojos y con los dedos ya indicados tapando los agujeros, déjelo caer y observe.
El agua no sale por los orificios y solo se moja el piso al chocar el envase contra él (¡Cuidado con los pies!).
Aquí pasó lo mismo que en el ascensor y que en las cápsulas espaciales. Esta y sus tripulantes están cayendo juntos hacia la tierra en dirección tangencial por su velocidad inicial dada por sus cohetes. El envase y el agua están cayendo juntos hacia el suelo y mantienen en todo momento igual velocidad y aceleración.
En el tratamiento del movimiento en una dimensión, cuando se trata de enseñar desplazamiento, velocidad y aceleración, tal vez en razón de la coincidencia en dirección de estas tres magnitudes vectoriales, se descuida recalcar este caracter. Recién cuando se analiza tiro oblicuo, como ejemplo de movimiento bidimensional, se hace notar a los alumnos que para indicar las mencionadas magnitudes es necesario usar vectores.
Luego se descomponen estas magnitudes en sus componentes y se estudian por separado, aplicando la independencia de movimientos en dos direcciones ortogonales entre sí.
Esto, se supone, simplifica el estudio, pero ¿se logra una buena comprensión del proceso en conjunto por parte de los alumnos?. Tal vez si el Profesor no deja de recalcar el aspecto vectorial del tema, logre que los alumnos tengan una mejor incorporación de la importancia tanto del módulo como de la dirección cuando de desplazamiento, velocidad y aceleración se trate.
Este artículo, destinado a Profesores, es para analizar el movimiento en dos dimensiones, fundamentalmente desde un punto de vista vectorial.
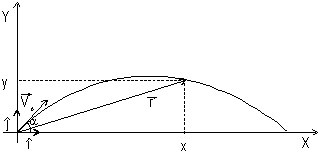 Recordemos que en el movimiento
en el plano se puede definir el vector posición r que va desde el
origen del sistema de referencia hasta la posición instantánea
del móvil.
Recordemos que en el movimiento
en el plano se puede definir el vector posición r que va desde el
origen del sistema de referencia hasta la posición instantánea
del móvil.
Se definen los versores i y j según los ejes x e y respectivamente,
y si son (x,y) las coordenadas del punto donde se encuentra el móvil,
se puede expresar:
r = x i + y j (1)
La velocidad instantánea se define como
![]() (2)
(2)
Y la aceleración:
![]() (3)
(3)
V es un vector tangente a la curva trayectoria. Las coordenadas (x,y) son funciones del tiempo. ¿Cuáles son estas funciones?.
Para obtenerlas se debe aplicar la segunda Ley de Newton.
F = m a (4)
En este caso F = -m g j , el peso del cuerpo.
Para iniciar este análisis se está suponiendo que la única
fuerza que actúa sobre el cuerpo es su peso. Reemplazando en (4)
![]()
Integrando
![]()
Siendo C1 = cte. de integración.
El valor de C1 es fácil de deducir, él es V0
pues para t = 0 la velocidad V tiene dicho valor.
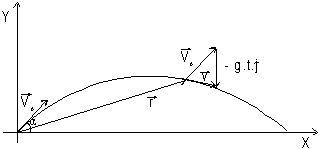
V = -g t j + V0 (5)
pero V0 = V0 cos a
i + V0 sen a j
V = V0 cos a i + (V0 sen a – g t) j (6)
escribiendo los componentes por separado, obtenemos las conocidas ecuaciones:
 Vx = V0
cos a Vy = V0 sen a
– g t (7)
Vx = V0
cos a Vy = V0 sen a
– g t (7)
Observe en la figura la representación de la ecuación (5).
Integrando nuevamente se obtiene x e y.
r = (V0 cos a) t i + (V0 sen a) t – ½ g t2) j (8)
la constante de integración es nula pues se supone que a t = 0, r = 0 (x = 0 e y = 0).
Al iniciar esta deducción se supuso que la única fuerza que actúa sobre el cuerpo es su peso. Sin embargo lo más común es que lo haga en un medio gaseoso, por ejemplo aire. Entonces aparecen fuerzas disipativas que modifican los valores teóricos de r y V.
Si el movimiento es de baja velocidad respecto a la velocidad del sonido,
la fuerza disipativa es proporcional a la velocidad y se opone al movimiento.
Esta fuerza disipativa se origina en la viscosidad del aire y se opone
en todo momento al vector velocidad instantánea. Por lo tanto la
ecuación (4) ahora adopta la forma
![]() (9)
(9)
![]() (10)
(10)
con ![]()
La (10) es una ecuación diferencial de segundo orden, lineal, a coeficientes constantes. Para resolverla apelaremos a caminos más largos, pero más sencillos.
La ecuación (10) se puede reescribir
![]() (11)
(11)
expresando V = Vx i + Vy j, reemplazando y separando
componentes en cada eje, se obtienen dos ecuaciones diferenciales.
![]() (12)
(12)
![]() (13)
(13)
En (13) ![]()
Vx = C1 e-k.t , para t = 0 Vx
= V0 cos a
entonces Vx = V0 cos a
e-k.t (14)
En (12) ![]()
Integrando ![]()
![]()
![]()
para t =0 ![]()
finalmente ![]() (15)
(15)
De acuerdo al desarrollo en serie de e-x, en este caso
![]()
Tomando los dos primeros términos y reemplazando
Vy = V0 sen a (1 – k.t) – g t (15)
Las ecuaciones (14) y (15) son las componentes del vector velocidad. Observe que cuando suponemos que el móvil se mueve en el vacío (k tiende a 0), estas ecuaciones se reducen a las ya conocidas de la bibliografía.
Para encontrar el vector posición, debemos encontrar sus componentes x(t) e y(t).
Aquí nuevamente hay dos caminos, el primero y más sencillo es integrar las ecuaciones de Vx y Vy, respectivamente y el segundo resolver la ecuación diferencial inicial (10).
El primer camino conduce a:
![]() (16)
(16)
![]() (17)
(17)
El segundo camino y partiendo de (10), conduce a la solución
![]()
Con A y B vectores cuyas componentes se deben obtener en base a los valores de r y V a t = 0 como ha sido hecho más arriba.
Las ecuaciones (16) y (17) dan las expresiones de las funciones x(t) e y(t), componentes del vector posición r(t), de ecuación (1).
Para comprobar que ellas incluyen el caso de tiro oblicuo en el vacío,
o sea k tiende a cero, reemplace la exponencial por el desarrollo en serie
indicado anteriormente y tome límite para k tendiendo a cero.
Editor: El Profesor de Ciencias, Departamento de Física,
Univ. Nac. de San Luis. C.C. 136 – CP: 5700 – San Luis