---

EL PROFESOR DE CIENCIAS

Número 7 FEBRERO/98

Facultad de Ciencias Físico Matemáticas y Naturales

Universidad Nacional de San Luis

---

OBJETIVOS

Esta publicación está destinada a Profesores de Nivel Medio en Matemáticas y Física.

El objetivo fundamental es establecer una comunicación directa de la Facultad de Ciencias Físico Matemáticas y Naturales (UNSL) con dichos Profesores, a efectos de desarrollar actividades que permitan mejorar la calidad de su enseñanza en estas ciencias y, por lo tanto, mejorar la calidad de sus egresados.

El contenido de esta publicación estará constituido por artículos metodológicos e instrumentales para la enseñanza teórica y práctica de temas del currículum de nivel medio, problemas y su metodología de resolución, desarrollo de temas de actualidad en relación a su aplicación al currículum, prácticos de laboratorio, preguntas y respuestas para transferencia de conocimientos, noticias de carácter educativo en el área, evaluación, cartas, comentarios y artículos enviados por los docentes-lectores, donde puedan aportar, solicitar o compartir sus logros, necesidades, dudas y, finalmente todo artículo cuyo contenido los profesores soliciten, sugieran o sea oportuno incluir.

IDEA Y REALIZACION: Lic. Carlos Magallanes

DISEÑO Y DIAGRAMACION: Dis. Graf. María Angélica Camargo
PUBLICACION EN FORMATO HTML: Prof. Germán R. Arias

Para lograr el propósito de mantener la edición de esta publicación, se necesita de la respuesta y colaboración de los destinatarios. Esto significa que es muy necesario, y se lo agradecemos desde ya, nos haga llegar sus opiniones, solicite y aplique el material que le ofrecemos, envíe artículos para publicar y difunda esta pequeña revista.
 

Partimos de la aceptación de que los problemas, en la enseñanza de la física, tienen como principal objetivo lograr de los alumnos habilidades en idear estrategias de razonamiento, organizar procedimientos, efectuar análisis crítico de resultados, y adquirir criterios de evaluación y estimación de situaciones físicas.

Para lograr esto los alumnos tienen que utilizar conocimientos teóricos que se supone ya conocen. El objetivo a largo plazo es que los problemas les enseñen a resolver futuras situaciones problemáticas en otras áreas del conocimiento o de la actividad humana.

A la luz de estas reflexiones, surge inevitablemente la pregunta ¿cómo tienen que ser los problemas de física para lograr estos objetivos?

Se ha hablado y escrito mucho sobre el particular, al igual que cuales estrategias utilizar para enseñarles a resolverlos.

Cualquiera sea la metodología siempre es necesario que haya un contenido tal que despierte en el alumno una motivación suficiente para que no se desanime en la tarea.

Para que haya contenido motivante tiene que serle familiar o estar vinculados a sus reales y actuales intereses.

Una alternativa para lograr esto es utilizar lo que se denomina "problemas ricos en contexto".

Estos problemas se diseñan de tal modo que el alumno se ve obligado a preparar una estrategia organizada en forma lógica y no puede aplicar las ecuaciones y obtener resultados en forma automática y sin comprender para qué lo hace, como comúnmente suele ocurrir. Todos sabemos que con esta práctica los alumnos no aprenden lo esencial de la física.

Estos problemas obligan al alumno a considerar y aplicar los conceptos físicos dentro de un contexto concreto insertado en el mundo real. Obliga al alumno a tomar una serie de decisiones. Otra característica importante de este tipo de problemas es que el alumno debe usar los conceptos en forma cualitativa, antes que una eventual aplicación a ecuaciones con cantidades.

Resumiendo, estos problemas tienen las siguientes características:

1. Cada problema es una breve historia en la cual el estudiante es, en lo posible, el principal protagonista.
2. El texto del problema incluye la apropiada motivación para que "Ud." o "tu" (el alumno) obtengan una respuesta.
3. Los objetos y situaciones deben, en lo posible, ser reales. Cuando es una situación imaginaria, se especifica en el texto como es el proceso de idealización.
4. No se dan figuras ni gráficos en el enunciado del problema. El alumno debe visualizar la situación y la información con sus propias habilidades e imaginación.
5. Los problemas no se pueden resolver en una sola etapa aplicando simplemente una formula y obteniendo una cantidad.
6. Estos problemas deben ser ideados de tal modo que obligue al alumno a tomar decisiones en base a sus conocimientos de los conceptos de física involucrados. Para esto el profesor debe tener cuidado de que el problema realmente se pueda resolver en base al conocimiento de los alumnos. Esto es importante por cuanto, en caso contrario, los alumnos se desmotivaron y el problema no podrá resolverse.
7. La respuesta que se pretende obtener del alumno, en lo posible no debe ser una cantidad. Si bien puede ser necesario que haga cálculos, procure que los resultados obtenidos sirvan como referencia para definir aquella.
8. Debe procurarse hacer comprender al alumno que resolver estos problemas es una tarea entretenida y satisfactoria cuando es lograda por ellos mismos. Para eso procure que trabajen en forma independiente y solo supervise que las decisiones no lo conduzcan a caminos sin salida.

9. La variable que se busca no está específicamente mencionada en el texto. El alumno debe descubrir que para contestar una pregunta, es necesario obtener el valor o comportamiento de una magnitud que no está específicamente mencionada en el texto.
10. Proveer más información de la necesaria. Esto es lícito por que es lo que sucede en la vida real y en cualquier área. Parte de la habilidad para resolver un problema en cualquier actividad es tener criterio para determinar la información relevante y descartar lo que no sirve para encontrar la solución. Pero debe cuidarse que ella aparezca en forma natural dentro del contexto real a que se refiere el problema.
11. Recíprocamente, puede faltar información. Será parte de la tarea del alumno, obtenerla en el proceso de resolución. Aquí se le debe enseñar que puede hacer una estimación de los valores de dicha información ausente o cómo buscarla en la bibliografía.
12. Obligar al alumno ha hacer suposiciones sobre condiciones del contexto vinculado al problema y con criterio de razonabilidad. Ellas no pueden ser arbitrarias. Además es conveniente que al concluir la resolución, el alumno tenga una idea de que modo la simplificación o condición supuesta aleja la solución de la que habría obtenido sin hacerla.
13. El problema requiere el uso de dos o más Principios o Leyes de la Física. Por ejemplo leyes de Newton más conservación de la energía.

¿ Cómo se crean problemas ricos en contexto real?

Las recomendaciones de la bibliografía consultada indican las siguientes etapas:

Parta con un problema de un texto. Luego modifíquelo teniendo en cuanta las siguientes recomendaciones.

1. Invente una breve y creíble historia. Describa el entorno, contexto y situación donde se ha presentado el problema. Procure en la medida de lo posible que esté lo más próximo posible a la realidad, intereses y actividades de sus alumnos.
2. Coloque en el centro de esta historia y contexto como protagonista principal al alumno. Utilice la palabra "Ud." o "tu" en el texto del problema para comunicarse con él. Recalque que él y sus compañeros de grupo deben resolver la situación.
3. Decida como generar motivación en el alumno para que este junto a su protagonismo generen una dinámica en el grupo que los motive a trabajar. Para esto es conveniente que adapte la historia a hechos reales y actuales, intereses particulares, permanentes o circunstanciales, de los alumnos o del grupo.
4. Determine el nivel de dificultad del problema en función del conocimiento que los alumnos tienen del o de los temas involucrados. Aquí deberá definir que información incluirá en el texto, cual omitir, si hace mención o no a la magnitud a determinar, etc.
5. Pruebe Ud. a resolver el problema antes de dárselo a los alumnos. Hágalo tal cual estima que ellos lo plantearan. Prevea los posibles caminos inconducentes que puedan tomar. Este ensayo le sugerirá modificaciones en la historia creada, en los datos dados, en los que son extras y aquellos irrelevantes, en el modo de despertar la motivación, etc.
6. No diseñe problemas con excesiva dificultad. No incluya todas las características anteriores en un solo problema. Incluya sólo algunas y en problemas distintos. Estos problemas deben ser pensados para ser resueltos por grupos de alumnos y no en forma individual. Esto en razón de que se procura que los alumnos aprendan a trabajar en grupo, a contrastar opciones u opiniones, a mejorar propuestas y aportar ideas y tomar decisiones en conjunto.
7. Conviene que los problemas sean resueltos por grupos de dos o tres alumnos. Un número mayor disminuye el rendimiento y la participación.

Ejemplo 1:

Ud. pertenece al servicio de Inteligencia de la Armada. A efectos de cumplir una misión secreta ha sido embarcado en un submarino con las instrucciones en un sobre cerrado. Recién lo podrá abrir en alta mar. En base a ellas deberá indicar al capitán del submarino el rumbo y la velocidad.

Las instrucciones son que el submarino que Ud. tripula se debe encontrar con otro similar en alta mar y en un punto determinado del océano Atlántico. Se le informa que el otro submarino partirá a la misma hora que Ud. y de un puerto que está a la misma distancia del punto de encuentro que el suyo.

Además se le informa que el otro submarino recorrerá los primeros 500 Km. a una velocidad de 20 Km./h, luego igual distancia a 50 Km./h., otros 500 Km. a 60 Km./h y finalmente los últimos 500 Km. a 40 Km./h.. Su submarino debe viajar a una velocidad constante.

El capitán ya determinó el rumbo en base a las coordenadas, ahora espera que Ud. le indique la velocidad.

Ejemplo 2:

Ud. es un reconocido atleta de su colegio. Su especialidad son las carreras de 5000 m.. Se aproximan las Olimpíadas Intercolegiales y en esta oportunidad Ud. quiere ganar la medalla para su Escuela. Su problema es vencer al campeón del Colegio Nacional. Siempre gana. Pero esta vez no será así. Para entrenarse los atletas utilizan el circuito del Lago Potrero de los Funes pues tiene una longitud de 5300 m.

Una tarde de entrenamiento se cruza con él mientras ambos practican en dicho circuito. Su entrenador (un compañero de curso) observa la hora del cruce: 17 h 30 min. Entonces Ud. decide ver como anda el promedio de su contrincante. Por anteriores carreras sabe que el siempre corre a 7 km/h. Lo vuelve a encontrar a las 17 h 38 min. ¿Qué información obtiene con estos datos?. ¿Cómo anda su adversario?. ¿Ha mejorado o empeorado su rendimiento?.
 
 

Ejemplo 3.

El próximo lunes 17 de Agosto será la marcha de los estudiantes de la Ciudad de San Luis al Monumento al Soldado Puntano de la Independencia, en Las Chacras. Ud. en el último partido de fútbol ha sufrido una lesión en el tobillo que le impide caminar normalmente. Pero como no se quiere perder el picnic posterior a la marcha decide ir en moto. De paso lleva los bolsos con las provisiones, las bebidas, el fútbol y la guitarra.

Sus compañeros partirán a las 7 hs y planean llegar al Ave Fenix a las 8 hs. Allí descansaran 30 minutos y luego en una sola etapa llegarán al monumento a las 10 hs. Ud. piensa ir en su moto a velocidad constante de 50 km/h. Como no le gusta esperar quiere llegar justo cuando lo hagan sus compañeros. Debe decidir a que hora partirá.
 
 
 
 

Ejemplo 4.

Ud. se encuentra en el punto de llegada de una carrera de bicicletas. Un señor se le acerca y le pregunta a qué distancia se encuentra el punto de partida, a lo que Ud. contesta que no sabe, pero lo invita a averiguarlo.

En ese momento llega el primer corredor. Uds. se le acercan y le preguntan: ¿a que distancia está el punto de partida?. El ciclista muy agotado les responde que no sabe, pero que él vino a una velocidad constante de 62 km/h. Pasa un rato y llega el segundo corredor. Uds. se acercan y le preguntan: ¿a que distancia está el punto de partida?. Les contesta también (muy agotado) que no sabe, pero que él vino a una velocidad constante de 56 km/h. El señor que le hizo la pregunta se le ocurre que es mas fácil y seguro preguntarles a los organizadores. Al rato vuelve y le comenta muy indignado y desanimado que ellos tampoco lo saben, solo saben que el primer corredor llegó a las 11 hs 15 m 20 s y el segundo a las 11 hs 18 m 26 s.

¿Puede Ud. con estos datos ayudar al señor a averiguar que distancia hay al punto de partida?.
 
 

Ejemplo 5.

Un amigo suyo tiene un serio problema. Tan serio que está por ir a ver a un psicólogo. Como el sabe que Ud. es buen alumno de Física, decidió comentarle antes a Ud. a ver si le ahorra el largo tratamiento a que inevitablemente le someterá este profesional.

Le relata que este verano pasó sus vacaciones en la playa y que un día ventoso (la radio dijo que la velocidad del viento era de 16 km/h), estando parado frente al mar mirando las olas y mojándose los pies, a un niño que se encontraba a 20 m a su derecha y al cual el agua le mojaba los pies, se le escapa una pelota que el viento se lleva mar adentro. El niño comienza a llorar y todos le gritan (a su amigo) que nade para alcanzarla. Si bien él es muy buen nadador (su marca es 2,5 m por segundo), consideraba que alejarse más de 30 mts de la costa era peligroso. Por eso se quedó parado y mirando como la pelota se alejaba. Además contó que el viento era perpendicular a la playa y en sentido hacia mar adentro y que la pelota avanzaba a la mitad de la velocidad del viento. Lo que el amigo quiere saber es si hizo bien en quedarse parado o debió lanzarse tras la pelota y regresar a la playa. ¿Puede Ud. con estos datos, ayudarle a resolver su complejo de culpa?.
 
 

Ejemplo 6.

Ud trabaja como asistente de un técnico de Telefónica de Argentina. Su trabajo es transitorio, por lo tanto Ud. es mas un aprendiz que un técnico. Un día su Jefe se enferma y sucede una emergencia en un segmento de línea, pues se han cortocircuitado los cables en algún punto a determinar. La línea está formada por dos conductores iguales pero aislados entre sí. En algún lugar se han pelado los conductores y están en contacto. Esto hace que el segmento de línea no permita funcionar a los teléfonos que ella une.

Ud. habla con su jefe (por teléfono por supuesto) y este le dice que desconecte los dos terminales de ambos extremos de la línea. Luego con una batería de 6 v. y un amperímetro mida la corriente desde ambos extremos de la línea. Además le avisa que la línea en falla tiene 1600 mts de longitud. Ud. hace lo que le indican y obtiene una medida de 1 A desde un extremo y 0,33 A del otro. Con estos datos Ud. determinó la ubicación del punto de falla. ¿Puede Ud. y su grupo, explicar a la clase como utilizan esta información para resolver el problema?.

A medida que se van desarrollando temas del programa de un Curso de Física, es conveniente implementar prácticas, en problemas y laboratorio, que integren varios temas.

Es frecuente encontrar que los problemas y los experimentos son verificaciones de un principio y se agotan en el tema mismo.

Esta aislación de temas es perjudicial para el esquema conceptual del área de la Física que el programa contiene. Si se integran los temas, el alumno tendrá una imagen mas sencilla de la jerarquía de Leyes, Principios y Fenómenos que ha estudiado y fundamentalmente las relaciones que los vinculan.

La presente sugerencia experimental vincula el Principio de Conservación del Impulso y el Teorema Trabajo-energía, para obtener la velocidad de una esfera que desciende por un plano inclinado. Además se ofrecen dos alternativas para verificar el resultado.

El material necesario es:

• una regla de plástico acanalada de unos 30 cms. de largo.
• un tablero rectangular rígido de madera con una superficie plana y bien pulida. Por ejemplo madera cubierta por fórmica.
• una esfera de acero de unos 2,5 cms. de diámetro. Su superficie debe estar limpia, seca y bien pulida.
• una cajita de cartón como las de cigarrillos, con la tapa superior y el frente removidos. La cara que queda se apoyará en el tablero y deberá deslizar sobre él, por eso cuide que esté limpia, sana y sin rugosidades.
• plastilina ablandada y coloreada en el interior de la caja como muestra la figura.
• regla y cronómetro.

El práctico consiste en determinar la velocidad Vo con que llega la esfera al pié de la regla, la que se encuentra apoyada en un extremo y levantada en el otro (ver figura).

Cuando la esfera llega al final de la regla sigue por el tablero, entra a la caja y se adhiere a la plastilina. A causa de la interacción la caja se deslizará una cierta longitud x y se detendrá. Esta distancia x debe medirse.

Si indicamos con V la velocidad con que arranca el sistema caja + esfera, por el teorema trabajo-energía, se cumple:
 

Siendo F la fuerza de rozamiento entre la caja que desliza y el tablero. Dada las bajas velocidades con que estamos trabajando, es una buena aproximación suponerla constante.

En el apéndice se sugiere un modo de medir la fuerza de rozamiento F.

Al aplicar el Principio de Conservación del Impulso, tenemos:
 

De aquí se puede calcular Vo.

Si el práctico terminara aquí, nada hay que asegure a los alumnos que han verificado los principios utilizados. De algún modo hay que confirmar este resultado.

Hay dos formas simples de hacerlo.

La primera es medir la velocidad Vo sobre el tablero en un segmento que esté muy cerca del borde apoyado de la regla. Con regla y cronómetro, y como promedio de varios lanzamientos desde la misma posición, se puede determinar Vo.

Otra forma es el tiro horizontal. Acerque el extremo apoyado de la regla a unos 5 cms. del borde de una mesa horizontal. Cuide que la inclinación de la regla siga siendo la misma.

Una vez que la esfera alcance el borde de la mesa caerá la altura Y de ésta, y a una distancia X de este borde. Midiendo X e Y se puede obtener Vo.

Observe que se puede modificar el orden de trabajo sugerido. Esto es calcular Vo como se ha indicado en la verificación y luego con este valor y el de F calcular V usando las ecuaciones (1) y (2). Teóricamente deben ser iguales. Pero inevitablemente surgen diferencias entre ellos por los errores experimentales. Diferencias no mayores del 5% son aceptables.

Como Ud. comprenderá es mejor no hacer el práctico si se van a obtener resultados disparatados. Para que esto no suceda, es obvio que lo que debe ensayar previamente, tanto para hacer un plan de trabajo para los alumnos, para seleccionar el material apropiado y asegurarse que los resultados serán aceptables.
 
 

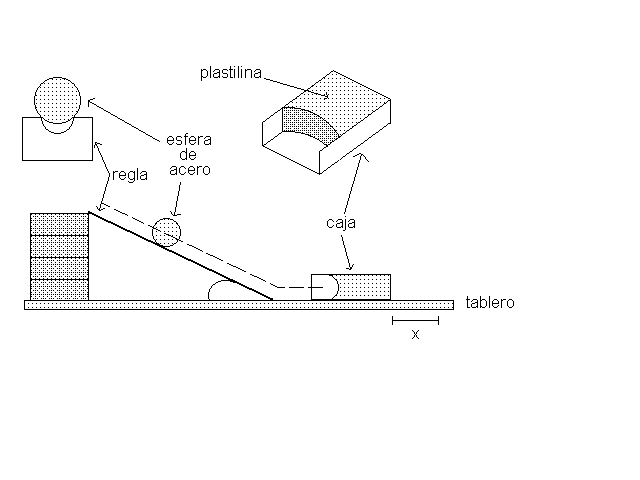
Apéndice: Medición de F.

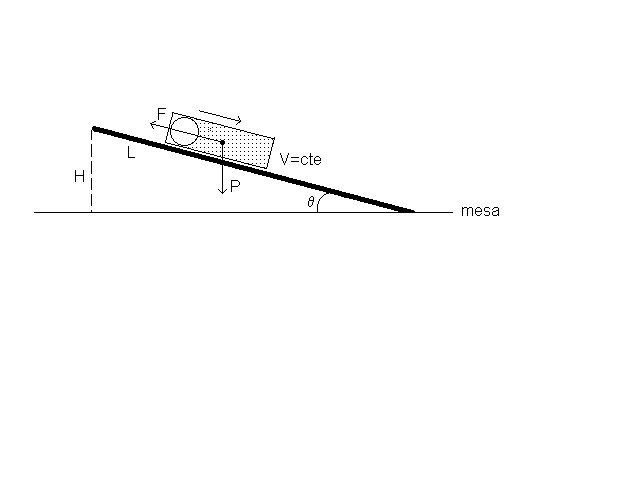
Para medir F coloque la caja con la plastilina y la esfera adherida a ella en el medio del tablero.

Con este apoyado en la mesa levante un extremo mientras el otro permanece apoyado. Continúe levantando lentamente hasta observar que la caja desliza con velocidad constante. Con regla y cronómetro puede verificar si lo desea la repetibilidad de la velocidad. Con los datos longitud del tablero (L) y altura (H) levantada puede deducirse que:
 
 

ó

Sea un cuerpo situado a una cierta altura próxima a la superficie terrestre. Si es dejado libre empieza a moverse según la vertical con un movimiento que suele denominarse "caída libre". Esto no es cierto, salvo que la caída se efectúe en un absoluto vacío. La llamada "caída libre", los alumnos no la ven, tal vez nunca, en su vida diaria. Por lo tanto enseñar este tema sin analizar la caída real de los cuerpos corre el riesgo de generar confusión y no ser comprendidas. Los alumnos ven que las cosas suceden de un modo distinto a lo que afirma el Profesor.

Este, tal vez se justifique "yo les advertí que eso es el vacío". De acuerdo, pero los alumnos en sus primeros estados de aprendizaje se manejan con lo concreto. Si Ud. tiene un tubo en el que puede hacer un buen vacío los convencerá con una demostración, en caso contrario es difícil que lo logre.

Para hablar más cómodamente convengamos en llamar caída libre a la que se produce en el vacío y caída gravitatoria a la que se produce en un fluido (líquido o gaseoso).

Respecto a la caída libre, no creo necesario hacer ningún comentario.

¿Qué pasa en una caída gravitatoria?

Simplemente que sobre el cuerpo actúa, además de la fuerza peso, la fuerza de arrastre, o de resistencia generada por el "rozamiento" con el fluido. Esta fuerza de arrastre tiene sentido opuesto al de la velocidad del cuerpo y su intensidad depende de ésta. También depende de la viscosidad del fluido y de la forma del cuerpo.

Cuando la velocidad del cuerpo es baja, la dependencia de la fuerza de arrastre con aquella es lineal. Para grandes velocidades la dependencia es cuadrática.

La relación entre la fuerza peso y la de arrastre es la que define en cuanto se aparta la caída gravitatoria de la caída libre.

Supongamos dos pelotas pulidas de exactamente el mismo tamaño, siendo una de telgopor y la otra de acero. Ambas son dejadas caer simultáneamente desde la misma altura. La pelota que encuentra mayor resistencia es la de acero pues se mueve más rápido a causa de que la aceleración que genera la resultante de la fuerza peso y la de arrastre es mayor para ella que la correspondiente que actúa sobre la de telgopor. Si la mayor resistencia del aire sobre la pelota más rápida es pequeña comparada con su peso, ella no afectará demasiado la aceleración resultante. Para la pelota liviana sucede al revés. Por lo tanto la de acero llegará al suelo antes que la de telgopor.

La dependencia de la fuerza resistente con la velocidad es la causa de que un cuerpo en caída gravitatoria alcance una velocidad límite. A partir de ese momento el cuerpo cae con movimiento uniforme, ya que su aceleración es cero, puesto que la fuerza resistente aumenta hasta un valor que iguala a la fuerza peso. Esto es fácilmente visible en un tubo largo lleno de glicerina cuando se deja caer una esferita de plomo de determinada altura.

En los textos, en general, el tema de la caída gravitatoria se evita y se trata solamente la caída libre.

Yo considero conveniente que el profesor haga una aclaración convincente de lo que sucede realmente, más allá de que luego suponga que la fuerza resistente es la suficientemente pequeña respecto del peso, como para no tenerla en cuenta.

Otra confusión semejante a la anterior se produce con la llamada "ingravidez". Cada vez que los noticieros en la televisión muestran imágenes obtenidas en naves espaciales en órbita, inducidos por estos o por los comentarios de los reporteros, muchas personas deducen que los astronautas están sin peso, por eso flotan junto con sus herramientas.

Genere en clase y de algún modo con sus alumnos la situación que conduzca a analizar esta cuestión.

Para aportar elementos de discusión puede apoyarse en las siguientes consideraciones:

1. Analizar que se quiere significar con peso de un cuerpo.
2. Puntualizar que la fuerza peso es un caso particular de la fuerza de atracción gravitatoria y cuya expresión general está dada por la ley de Gravitación Universal de Newton.

 

 
 






 






Con Mt = masa de la tierra, Mc masa del cuerpo, y R la distancia entre el centro de la tierra y el centro del cuerpo.

3. mediante cálculos mostrar que, por ejemplo para que un cuerpo que pesa 1000 Nt en la superficie terrestre, reduzca 10 veces este "peso" debe alejarse alrededor de 2,2 veces el radio terrestre (o sea unos 16000 Km).
4. hacer notar que las misiones espaciales se ejecutan en órbitas a una distancia del orden de 300 Km. de la superficie terrestre de lo que se deduce que la reducción de la fuerza peso es muy pequeña. O sea que los astronautas en órbita pesan un poco menos que en la superficie terrestre.
5. hacer notar que el cálculo hecho en c) es una situación estática, en cambio la que se ve en TV es una situación dinámica en la que está involucrado movimiento.
6. Este movimiento de los satélites en realidad es el de un cuerpo cayendo, prácticamente en caída libre. La diferencia con las esferas del principio de este artículo, es que tienen una velocidad horizontal.
7. Repase el experimento imaginado por Newton y que hoy el hombre y su tecnología han concretado. Newton imaginaba que si un cuerpo se lanza desde una cierta altura con una velocidad horizontal creciente, llegará un momento en que esta velocidad será tal que permiten que el cuerpo, siempre cayendo hacia la tierra, logre dar una vuelta completa.
8. mientras el cuerpo está recorriendo esta órbita alrededor de la tierra, el está permanentemente cayendo. Si el cuerpo es un satélite con tripulación, esta también cae con la misma aceleración que la nave. Si uno de ellos deja suspendido en el interior de la nave una herramienta, ella permanecerá en ese punto, como si no tuviera peso, pero continua con la misma velocidad del tripulante y la nave cayendo hacia la tierra. Esta observación de que las cosas "flotan" en el espacio conduce a la falsa deducción de que ellas, en esta situación, no tienen peso.


Es necesario advertir a los alumnos de no cometer este error conceptual. Dicho de otro modo: no dejarse engañar por las apariencias.

9. Se puede realizar un experimento, pero a causa de su peligrosidad no es recomendable. También es difícil de implementar. Consiste en encontrar un edificio con una buena cantidad de pisos subir a un ascensor, y con el ir hasta el último piso, llevar una balanza de baño y una bola de cualquier material. Una vez allí arriba subir a la balanza y sostener la bola con la palma de la mano. Una vez listo pedir al ascensorista que deje descender el ascensor en caída libre (o sea con g = 9,8 m/s2). Mientras va cayendo y si el pánico no lo domina, retire la palma de la mano de la esfera verá que ella sigue allí como si no tuviera peso. Si mira la balanza verá que marca cero. Obtuvo el régimen perfecto para adelgazar. Además podrá percibir la sensación de falta de peso o ingravidez. Esto es lo que pasa en un satélite artificial con las cosas y sus tripulantes. Cuando el ascensorista retome el control y empiece a frenar hasta detenerlo verá que la balanza otra vez marca su peso y que la bola se encuentra en el piso del ascensor.

Imagínelo, pero no procure realizarlo.

El tema tiro oblicuo (en la superficie terrestre) está presente en la mayoría de los programas de Cinemática de nivel medio.

Entre las principales conclusiones que obtienen los alumnos es que la trayectoria del proyectil obedece a la ecuación de una parábola, con eje vertical y la concavidad hacia abajo.

El Profesor de Física los convence de esto y a veces les deduce la expresión de la curva mencionada.
 
 

Los parámetros que deciden la altura y alcance horizontal máximo son el ángulo del lanzamiento q medido desde la horizontal y el módulo del vector velocidad inicial (Vo) del proyectil.

Por su lado g = aceleración gravitatoria, es una constante para el lugar.

Puede suceder que el alumno se encuentre tiempo después con el Profesor de Matemáticas (a veces la misma persona que les enseña Física) desarrollando el tema cónicas o curvas de segundo grado.

Le mencionará la circunferencia, la elipse, la hipérbola y la parábola, al menos.

De cada una de ellas le dará una definición, una ecuación, definirán elementos, características, etc.

Cuando llegue a la parábola, es probable que al alumno le suene de algún modo la palabra o la forma de la curva. También, es muy probable que el Profesor no le mencione para nada que relación hay entre ésta parábola y la que vió en tiro oblicuo.

Si el alumno es de los que van al frente le hará una pregunta, en mayor o menor medida, en los siguientes términos:

¿Qué tiene que ver esta parábola que Ud. define con la que vimos en tiro oblicuo?, ¿Dónde están en aquella la directriz y el foco?, ¿Tienen algún significado físico?.

Veamos aquí de analizar la respuesta.

Una parábola con el eje coincidente con el eje y, y cuyo vértice se encuentra en el origen de coordenadas obedece a la ecuación:
 
 

Si p>0 la curva se encuentra en y>0. Para p<0 sobre y<0.

Si la curva está desplazada, de tal modo que su eje sigue siendo paralelo al eje y, y si el vértice tiene coordenadas (a,b), la ecuación (2) se transforma en
 

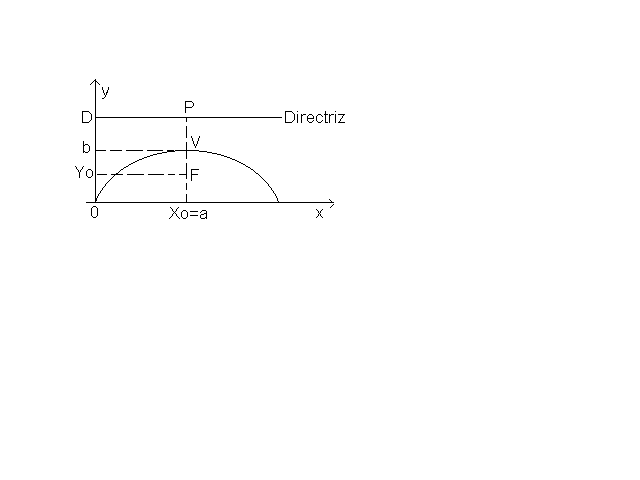
En la figura se representa una parábola, con eje paralelo al y, la recta directriz (D), el foco (F), el vértice V. Por definición PV = VF = p/2. Con (Xo, Yo) se indican las coordenadas del foco, con D la distancia del origen 0 a la recta directriz.

De la figura se deduce que a = Xo, b = Yo + P/2 , p = D – Yo reemplazando y operando en (3)
 
 

Si la parábola pasa por el origen se cumple que D² = Xo² + Yo², pues, entonces se encuentra a igual distancia de la mediatriz que del foco F.

La ecuación se reduce a
 
 

Comparando los coeficientes de igual grado de las ecuaciones (1) y (4) se deduce

Despejando  (5)
 
 

Pero Yo + p/2 = altura máxima alcanzada por el proyectil
 
 

O sea: 

Reemplazando en (5) resulta:  (6)
 
 

Obsérvese que la ordenada de la directriz de la parábola es la altura que alcanzaría el proyectual si se lo lanzara verticalmente con la misma velocidad inicial Vo.

Para obtener la coordenada del foco (Xo, Yo) observemos que si no hay rozamiento que deforme la parte final de la parábola, la abscisa Xo está en el punto medio del alcance horizontal Xm.

O sea

(7)

(8)
 
 

La ecuación (9) afirma que el ángulo que el vector posición del foco forma con la dirección del lanzamiento (q ) es igual a la que forma ésta con el eje vertical.

De (9) o de (8) se puede deducir que el foco F estará por encima del eje horizontal X cuando q > 45º, cuando q = 45º sobre este eje y por debajo (Yo < 0) cuando q < 45º.

Estas deducciones han sido realizadas siguiendo las ideas del autor mencionados en la bibliografía y son expuestas aquí con el ánimo de ofrecer a los Profesores de Matemática y Física una oportunidad para mostrar a sus alumnos que lo que enseñan ambos profesores está a veces muy vinculado.

Cuando se enseña el tema ondas mecánicas, casi inevitablemente se usan como ejemplo las ondas en la superficie del agua y con menos frecuencia se las visualiza con una cubeta de ondas.

En la experiencia inicial se insiste a los alumnos que las ondas, cuando se propagan, transportan energía y no masa.

Aparentemente las ondas en el agua son transversales, esto es, la superficie libre asciende y desciende verticalmente a medida que la onda pase por el punto observado.

Pero cuidado, las ondas en la superficie del agua no son transversales, tampoco son longitudinales, sino una combinación de ambas.

Consideremos un canal rectangular muy largo y de profundidad h, conteniendo agua. Además un sistema de referencia con su eje x en la superficie del agua y con dirección coincidente con el eje del canal.

El origen del eje y también está en la superficie libre del líquido.
 
 

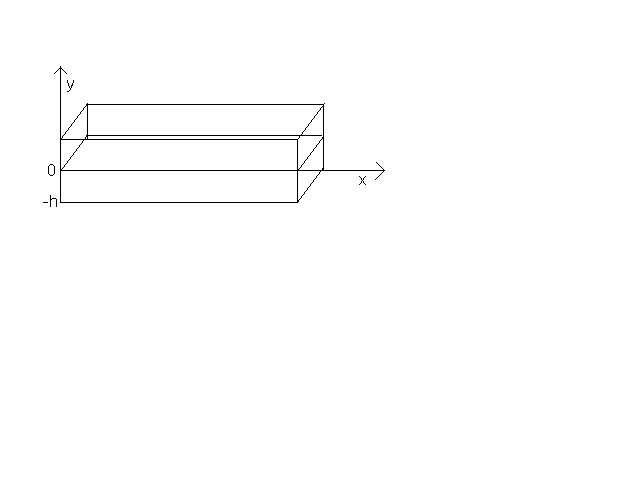
Sin embargo es necesario tomar en cuenta dos propiedades del agua para analizar la propagación de ondas en su superficie.

Una es la incompresibilidad. Su bajo valor del coeficiente de compresibilidad (@ 5.10^-10 m² N^-1) hace que, por ejemplo en la base de una columna de agua de 1 mt. de altura, la densidad cambie en menos que 0,05%. Es claro que es una buena aproximación suponerla incompresible cuando se estudian ondas de pequeña amplitud. La facilidad con que los fluidos fluyen depende de su viscosidad. Ello es la causa de la atenuación progresiva de las ondas hasta su anulación.

La incompresibilidad del agua es la que determina que las ondas no sean transversales. Imaginemos un pequeño volumen que se desplaza hacia abajo en algún punto de la superficie. En consecuencia, el agua que se encuentra debajo de este volumen debe desplazarse lateralmente hacia una zona donde el agua se haya desplazado hacia arriba.

El agua no puede moverse simplemente hacia arriba y abajo como un resorte compresible. Cada partícula de agua debe moverse en dos direcciones o sea en la dirección x e y del sistema que hemos elegido.

Por lo tanto debemos definir una función F que será función de las coordenadas x e y, y del tiempo t. F(x,y,t). Cuando la onda pase desde el punto de coordenadas (x,y) al instante t a una nueva posición (x’,y’) al instante t’, la función F(x’,y’,t’) indica la nueva posición de la partícula.

Podemos definir F_x(x,y,t) y F_y(x,y,t) para indicar el desplazamiento en dirección x e y respectivamente de la partícula respecto de la posición de equilibrio.

Si suponemos el caso mas simple de que el generador de ondas efectúa un movimiento armónico simple, las ondas que se propagan serán senoidales, o sea la Fx y Fy tendrán argumentos que contengan la función seno (o coseno) y variarán en forma armónica, con una frecuencia dada por el generador.

Por lo tanto el movimiento de cada partícula es la superposición de dos movimientos oscilatorios armónicos en direcciones x e y, respectivamente y de igual frecuencia.

Dado que hay un movimiento neto de la onda en dirección de x, deberá aparecer en la fase de Fx y Fy un término Kx que de cuenta de esta propagación.

Por otra parte, como Fx y Fy tienen argumentos armónicos y si bien tienen igual frecuencia, ¿hay entre ellos una diferencia de fase?. Si, la hay y es p /2. Observen al punto medio entre un máximo y un mínimo de la onda. Allí la superficie tiene la máxima pendiente y Fy=0. La partícula se ha desplazado hacia la derecha a causa del ascenso de las partículas a su izquierda y descenso de las de su derecha. Luego, las primeras empiezan a descender y las segundas a subir, por lo tanto de esta partícula en observación empiezan a retroceder. Esto significa que cuando Fy=0, Fx es máximo y recíprocamente. Dicho de otro modo, tienen una diferencia de fase de p /2.

Se puede sintetizar lo anterior escribiendo para Fy y Fx.
 
 

Las amplitudes de Ay y Ax dependen, según se puede demostrar, solo de y.

De (1) y (2) se puede deducir que para todo (x,y,t)
 
 

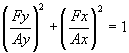
Esta es la ecuación de una elipse, con semiejes en dirección x e y, y centro en el punto (x,y).

Esto significa que la trayectoria de una partícula de agua cuando se propaga una onda senoidal en su superficie es una elipse en un plano vertical a la superficie y centrada en el punto de equilibrio de la partícula. Los semiejes de esta elipse se encuentran uno perpendicular a la superficie y el otro paralelo a ella.

La excentricidad de la elipse depende de Ax y Ay.

Los movimientos del fluido son mejor expresados con la velocidad que con el desplazamiento. La velocidad se puede medir, en cambio, el desplazamiento de cada partícula no.

Por eso restringiendo lo siguiente a modo de ondas de pequeña amplitud, se pueden obtener los componentes del vector velocidad, diferenciando las ecuaciones (1) y (2).
 
 

Vy(x,y,t) = -wAy sen(Kx-wt)
 
 

Vx(x,y,t) = -wAz cos(Kx-wt)
 
 

Para demostrar que cada partícula de agua, al pasar la onda senoidal obedece a las ecuaciones anteriores, y que su trayectoria es una elipse, se supone la incomprensibilidad y la no-viscosidad del líquido.

Al aplicar la incompresibilidad se puede demostrar que el flujo de velocidad a través de las caras de un cubo, imaginariamente inmerso en el líquido satisface la ecuación

(3)
 

 

En términos corrientes significa que lo que entra de fluido al cubo, necesariamente sale la misma cantidad por otras caras.

La condición de no-viscosidad asegura que cada volumen de agua no adquiera movimiento angular, de tal modo que no se puedan generar remolinos o vórtices. Si la viscosidad fuera considerable, fuerzas de corte generarían la rotación del volumen de líquido y por lo tanto la presencia de remolinos.

La forma matemática de poder expresar esta restricción es decir que la circulación del vector velocidad alrededor de cualquier trayectoria cerrada en el líquido sea nula.

En forma de ecuación se puede expresar:
 
 

ó rotor V = 0 (4)
 
 

Las ecuaciones (3) y (4) mas dos condiciones de contorno permiten obtener las expresiones de Ay y Ax. Estas expresiones nos permiten definir las formas de las elipses y de que estas dependen.

Las condiciones de contorno que se imponen son:

1. en la superficie (y=0) la función Fy debe coincidir con la función total F(0,x,t) = Acos(Kx-wt) que describe la propagación de una onda senoidal en dirección x.
2. En el fondo del canal (y=-h), las partículas que están en contacto con él, no pueden tener movimiento vertical, por lo que allí Fy(x,-h,t)=0

Siendo senh y cosh, el seno y el coseno hiperbólico.

La relación:

nunca puede ser mayor que 1. Por lo tanro Ay(y) < Ax(y), esto significa que la elipse tiene su eje mayor en la dirección x. El aplastamiento de la elipse se hace más pronunciado a medida que aumenta h. Las partículas de agua en el medio del canal se mueven horizontalmente y periódicamente a lo largo de un segmento de longitud 2Ax. También el movimiento horizontal disminuye en amplitud, con la profundidad, aunque mas lentamente, pues el cosh disminuye más rápidamente que el senh para valores negativos de y.

Hemos visto entonces, que las partículas al pasar las ondas, efectúan movimientos oscilatorios superpuestos y en direcciones perpendiculares entre si, de tal modo que este movimiento compuesto les hace recorrer una elipse.

¿En qué sentido lo hacen?.

Las ecuaciones que dan Ax(y) y Ay(y) permiten deducir que siempre son positivas pues (h+y) nunca puede ser negativo. Con esta observación y analizando las ecuaciones (1) y (2), se deduce que Fx atrasa p /2 respecto de Fy. Por lo tanto las partículas recorren las elipses en el sentido horario para una onda que avanza hacia la derecha.
 
 

Influencia de la profundidad

Consideremos dos casos extremos:

1. aguas profundas.


Si el agua es profunda (h >> l ) y estamos interesados en lo que sucede en la superficie (|y| << h), se pueden hacer las siguientes aproximaciones:
 
 


 
 


 
 

Las expresiones para Fx y Fy se reducen en este caso a:
 
 




 
 

Se ve que las órbitas son prácticamente circulares a todas las profundidades. El diámetro se va reduciendo exponencialmente a medida que aumenta la profundidad, siendo despreciable a profundidades 

Las ondas en aguas profundas, no perturban a éstas, en profundidad, mucho más allá que unas pocas longitudes de onda.
 
 

2. Agua poco profunda

Senh Kh @ Kh
 
 

Senh [K(h+y)] @ K(h+y)
 
 

Cosh [K(h+y)] @ 1
 
 

Entonces la (1) y (2) se transforman en:
 
 

Fy(x,y,t) = A(1+y/h)cos(kx-wt)
 
 

Fx(x,y,t) = A(1/kh)sen(kx-wt)
 
 

La amplitud del movimiento horizontal es prácticamente el mismo a todas las profundidades. En cambio el vertical cae rápidamente respecto de su valor en superficie.

Por lo tanto estas ondas son prácticamente longitudinales. El agua oscila en dirección x, que es el de propagación. En estas condiciones las ondas en el agua y debajo de la superficie, son semejantes a las sonoras y a las ondas como en general se las estudia: oscilaciones en una única dirección.

Con excesiva frecuencia "la distancia" entre la Física que se enseña en el aula y la que está oculta en los fenómenos físicos, y que tal enseñanza pretende explicar, es tan grande, que los alumnos no pueden relacionarlas. Por eso el Profesor debe cuidar de enseñar Física con los pies en la tierra.

No debe volar con ecuaciones que poco y nada enseñan cuando solo se las aplica para obtener resultados numéricos. Ellas aportan mucha información cuando se las analiza en su contenido, sus límites de validez, sus relaciones con otras y como describen los fenómenos y modelos con las que están vinculadas.

Este volar por las "nubes de ecuaciones" solo logra que el alumno no comprenda a) lo que dice el Profesor, b) que es lo que éste le quiere decir, d) para que le sirve estudiarlas y e) que tienen que ver con los fenómenos físicos que se producen en su vida real.

Una consecuencia inevitable y lógica es la pérdida de interés, motivación por parte del alumno.

Todo lo anterior ya fué comprendido por las Ciencias de la Enseñanza hace mucho tiempo. Los profesores lo aprendieron durante su formación y lo verifican diariamente en su práctica docente. Sin embargo sigue sucediendo.

En esta publicación no se pretende criticar ni al profesor ni a su metodología. Se quiere ofrecerle elementos de trabajo, ideas e información que le ayuden a dar mejores clases y motivarles a buscar fuentes que les permitan mejorar su formación.

Consecuente con ello y con la falencia mencionada al principio, en este artículo se presentan una serie de preguntas que pueden surgir de un alumno ó que el Profesor puede utilizar como elemento de motivación ó aplicación en el desarrollo de un tema.

Se adjunta a cada pregunta, una respuesta posible.

La distribución al azar del sentido de los imancitos hace que la magnetización resultante de la cinta sea nula.

En un casette con la cinta grabada el proceso de grabación genera zonas microscópicas con una magnetización resultante en un sentido o en el otro.

Durante el proceso de grabación el micrófono mide los cambios de presión del aire asociado a la onda sonora y produce una pequeña corriente eléctrica fluctuante. Esta corriente se obtiene por inducción al desplazarse un pequeño imán dentro de una bobina, todo esto dentro del micrófono. Esta corriente eléctrica variable es luego amplificada por el grabador y es conducida electrónicamente a un electro imán que se encuentra en la cabeza grabadora.

Este electroimán magnetiza la porción de cinta que está pasando frente a él mientras dura esta corriente fluctuante.

Magnetizar, significa aquí, orientar las partículas magnéticas en una de las direcciones posibles a lo largo de la cinta. Mientras más grande es la variación de presión sonora frente al micrófono más intensa es la magnetización de la película magnetizable de la cinta.

Al finalizar la grabación, la parte utilizada de cinta queda dividida en pequeñas porciones (o regiones) con una magnetización no nula y con distintas profundidades y sentidos.

Durante la reproducción de la parte grabada de la cinta, ésta pasa frente a la cabeza lectora (a veces la misma cabeza grabadora). Como la cinta está magnetizada por regiones y con distintas intensidades y direcciones los campos magnéticos de ellas penetran en el electroimán generando pequeñas corrientes eléctricas inducidas. Esto, que se denomina inducción electromagnética, es debido a que cuando un campo magnético variable penetra por una bobina, se induce en ésta una pequeña corriente eléctrica. Esta pequeña corriente inducida es amplificada electrónicamente por el grabador y conducida para que actúe sobre los parlantes. Así se reproduce el sonido original.

Para borrar una grabación de una cinta grabada se utiliza la cabeza borradora. Esta consiste en un electroimán que aplica en la cinta un campo magnético alterno, o sea que cambia su orientación en un sentido y el opuesto, dejando las partículas magnéticas de la película en la cinta orientada en forma desordenada hacia un extremo ó el otro.
 
 

Hay una frecuencia a la que se produce la máxima absorción de energía por parte de la molécula.

Cuando se produce esta absorción máxima decimos que la molécula está resonando.

En el caso del agua, para que la molécula resuene, la frecuencia de la microonda debe ser próxima a 17 Ghz.

Sin embargo no sería conveniente un horno de microondas que trabaje a 17 Ghz, pues en tal caso la energía de estas ondas sería absorbida por las moléculas de agua próximas a la superficie del cuerpo que se encuentre en su interior.

La frecuencia de 2,45 Ghz para los microondas ha sido elegida porque ellas son débilmente absorbidas por las moléculas de próximas a ka superficie, reduciendo poco su intensidad, de tal modo que puedan seguir penetrando y cediendo energía a las moléculas que se encuentran en las zonas profundas del alimento en cocción.

Si la frecuencia fuera mas baja, si bien penetrarían mejor en el alimento, la energía absorbida por las moléculas de agua sería insuficiente para lograr la temperatura necesaria para la cocción

La frecuencia ya mencionada es una solución intermedia entre ambos extremos.
 
 

El volumen que ocupa el hielo es mayor que el que ocupaba el agua de la que se formó.

Por lo tanto al no haberse modificado el volumen del agua, a causa de la rigidez y no dilatabilidad del recipiente, no podrá formarse hielo.

Como el agua estaba a la temperatura ambiente al ir bajando la temperatura ésta se contrae.

Esto genera un vacío en el recipiente que es ocupado por vapor de agua. Esta contracción se produce hasta los 4° C. Por debajo de esta temperatura el agua comienza a expandirse, ocupa nuevamente el espacio vacío pero esta dilatación encuentra un límite dado por el volumen del recipiente. En consecuencia el hielo no puede formarse.

El hielo no puede formarse porque al expandirse el agua, y como el recipiente no cede volumen, la presión en el líquido aumenta. Este aumento de presión baja la temperatura de solidificación, por lo tanto el hielo no se forma.

Para que se forme hielo sería necesario seguir disminuyendo la temperatura por debajo de 0° C.
 
 

Estos gases se difunden por la atmósfera y pasan a integrar el smog que diariamente respiramos. Este smog es perjudicial para la vida de las personas, animales y plantas y aumenta el efecto invernadero. Al estimar la cantidad de automotores que circulan por el mundo, más la cantidad de motores fijos, todos ellos funcionando con combustible de origen fósil (petróleos), uno puede darse cuenta y preocuparse por la agresión que sufre el medio ambiente, hecho que finalmente influye en la salud del hombre y otros seres vivos.

Para reducir el impacto de esta contaminación, en algunos países es obligatorio que los automóviles al salir de fábrica, lo hagan provistos de convertidores catalíticos en su caño de escape.

Es una tendencia actual en la industria automotriz que todos los autos 0 Km. salgan con convertidor.

El convertidor catalítico es un tubo que contiene una sustancia cerámica con una estructura de "panel de abeja" distribuida a lo largo de él.

Incorporadas a esta estructura hay pequeñas partículas de platino y paladio. Cuando las moléculas del gas expulsado por el pistón pasan por este "panal de abeja" se depositan sobre las partículas brevemente. Allí se combinan con átomos de oxígeno para formar moléculas de agua o dióxido de carbono.

A causa de su contenido en partículas de platino y paladio los convertidores catalíticos son caros. Pero las partículas son claves en el proceso de neutralización de los gases contaminantes. Si estas partículas se contaminan, el catalizador pierde efectividad. Es lo que pasa con un catalizador puesto en un motor que usa nafta con plomo. Los gases de la combustión contienen plomo, éste se deposita en las partículas y así se anula su capacidad para retener las moléculas que se quiere neutralizar.

Los convertidores catalíticos trabajan a muy altas temperaturas a causa del pasaje de los gases calientes que llegan del motor. A este calor se suma el generado en la combustión controlada dentro del catalizador.
 
 

Si todo está quieto dentro del horno durante la cocción, se obtendría un producto cocinado en forma no uniforme.

Al girar la plataforma que contiene el alimento, se asegura que este pase por regiones de distintas "temperaturas" y así uniformar la cocción. Algunos hornos usan bandejas rotatorias y metálicas para dispersar las microondas y así movilizar los puntos de interferencia.
 
 

El valor de g, a nivel del mar, está determinado principalmente por la masa de la tierra, su radio R y la constante G de gravitación universal. recordemos que el peso de un cuerpo es la fuerza de atracción gravitatoria entre éste y la tierra y que su valor se obtiene de multiplicar la masa del cuerpo por g.

Por otra parte, de acuerdo al Principio de Inercia todos los cuerpos tienden a permanecer en reposo ó en movimiento rectilíneo uniforme (velocidad constante) si están libres de fuerza neta actuando sobre ellos. Si actúa una fuerza neta no nula se modificará el estado de movimiento del cuerpo. La acción de esta fuerza se detecta por la aceleración que sufre el cuerpo.

Recordemos la naturaleza vectorial de fuerza, velocidad y aceleración. Cambiar la velocidad, y por lo tanto acelerar, puede significar un cambio en dirección ó en módulo solamente ó un cambio en ambas características del vector velocidad. Ejemplo: un cuerpo en caída libre y otro en movimiento circular uniforme ambos están acelerados.

¿Qué sucede con nuestro cuerpo cuando es acelerado? Sus distintas partes tienen su inercia pero como el resto del cuerpo deben acelerarse también. La acción de la fuerza en estas distintas partes generan sensaciones que Ud. percibe. En general no son agradables.

Estas sensaciones son de una gravedad extra actuando sobre su cuerpo. Ud. no puede distinguir la gravedad verdadera de la aceleración extra que actúa sobre su cuerpo. La sensación de aceleración extra depende de la posición relativa de la fuerza peso de su cuerpo y la de la fuerza exterior. Por ejemplo si se encuentra sobre una plataforma horizontal rotatoria no sentirá sensación de peso extra pero si deberá hacer fuerza para mover una mano o levantar una pierna.

En cambio si la fuerza exterior actúa en dirección vertical como lo hace la fuerza peso, según que tengan igual u opuesto sentido tendrá sensaciones distintas.

Supongamos un ascensor que acelera hacia arriba, Ud. sentirá una sensación de peso extra hacia abajo, está experimentando una "g" positiva. Si por el contrario acelera hacia abajo, como cuando un ascensor frena para detenerse la sensación de peso apunta hacia arriba y Ud. experimenta una sensación de disminución de peso ("g" negativa).

Como la fuerza exterior puede tener cualquier valor se puede lograr que el cuerpo humano experimente varias veces "g" negativas o positivas. Sin embargo cuando estas sensaciones son pocas veces mayores que "g" las sensaciones son molestas y pueden provocar dificultades.

Supongamos que se encuentra viajando en su automóvil. Es un día calmo, no hay viento. La velocidad del vehículo es 40 km/h: Lleva la mano abierta fuera de la ventanilla de tal modo que la palma enfrenta al aire que ejerce presión a causa del movimiento.

• ¿Si se duplica la velocidad del automóvil, cuantas veces aumentó la fuerza sobre la palma de la mano?;

• ¿Cuánto debe aumentar la velocidad del automóvil para que la fuerza se duplique?