Audición
Autor:
Pedro Alfredo Velasco
1a. La Percepción de la intensidad
Si bien los sonidos comprendidos en un rango de
frecuencias que va de 20 Hz los 20.000 Hz producen sensación sonora, no es
cierto que el oído sea igualmente sensible a toda esta gama de frecuencias.
Otra forma de plantear esta situación sería que
no todos los sonidos de igual intensidad comprendidos entre 20y 20.000 Hz son
percibidos con el mismo nivel de sensación sonora.
Si bien en general es cierto que cambios en la
intensidad de un sonido (propiedad objetiva) producen variaciones en la
sonoridad acústica (propiedad subjetiva) de la sensación sonora, estas
variaciones dependen también de la frecuencia particular del sonido.
Es decir, la experiencia muestra que la
sonoridad acústica con la que el oído percibe un sonido depende de la
intensidad y la frecuencia de la onda sonora.
Más aún puede ocurrir que dados dos sonidos de
igual intensidad y distinta frecuencia uno de ellos sea audible y el otro no
aunque ambos pertenezcan al rango de frecuencias audibles.
Para cada sonido existe una intensidad mínima
por debajo de la cual no es percibido como sensación sonora. Esta intensidad
mínima constituye el umbral de audición, varía con la frecuencia y si bien no
toma el mismo valor para todas las personas es posible construir una curva como
la inferior de la Fig.1 que representa el umbral de audición para un oído
normal.
Este umbral constituye el mínimo de nivel de
intensidad que debe poseer un sonido para que sea apenas audible y pueda
diferenciarse del silencio.
A medida que aumenta la intensidad del sonido
aumenta la sonoridad de la sensación sonora hasta que, aproximadamente a los
130 dB para todas las frecuencias, el oído comienza a percibir una sensación de
dolor. Es lo que constituye el límite o umbral de dolor y está representado por
la curva superior de la Fig. 1.
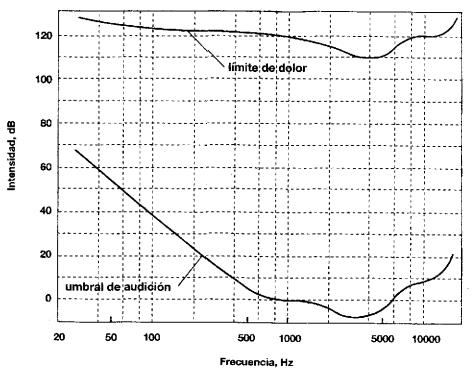
Fig. 1. Umbral de audición y límite de dolor para el oído normal
Estas dos curvas determinan claramente tres
zonas que se observan en la Fig. 2.
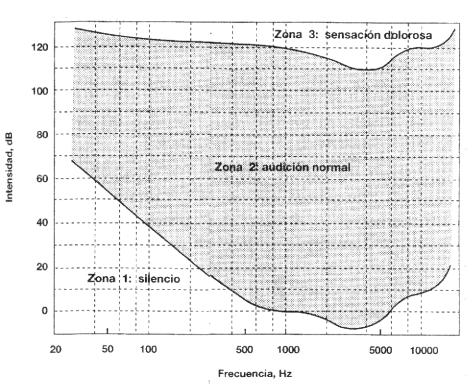
Fig. 2. Intervalo medio de audición normal
Los sonidos ubicados en la Zona 1, por debajo
del umbral de audición, no producen sensación sonora y no son percibidos por el
oído normal.
Los sonidos ubicados en la Zona 2 por encima del
umbral de audición y por debajo del límite de dolor producen sensación sonora y
son los sonidos naturalmente percibidos por el oído normal.
Los sonidos ubicados en la Zona 3, por encima
del límite de dolor producen una sensación dolorosa y son nocivos para el oído
provocando lesiones tempranas o permanentes dependiendo de la frecuencia, el
tiempo de exposición y el nivel de intensidad.
La Fig. 2 representa el intervalo medio de
audición y a partir del mismo puede observarse que:
·
Todos los sonidos que están por
debajo del umbral de audición no producen sensación sonora.
·
Todos los sonidos que están ubicados
en el umbral de audición son apenas audibles
·
Todos los sonidos que están por
encima del umbral de audición y por debajo del límite de dolor constituyen el
campo de audición normal.
·
Todos los sonidos que están en el
límite de dolor y por encima de él provocan sensación dolorosa y pueden causar
deterioro irreversible del oído interno.
·
Los sonidos ubicados en el umbral de
audición en general no tienen el mismo nivel de intensidad sino que el mismo
varía con la frecuencia.
·
Dos sonidos con igual nivel de
intensidad pero de distinta frecuencia no tienen necesariamente la misma
sonoridad acústica. Uno puede percibirse con más o menos sonoridad acústica que
el otro e inclusive puede no ser audible.
·
La línea que delimita el umbral de
audición puede variar levemente de persona a persona sin que ello implique
necesariamente la existencia de alguna anomalía.
1b Unidades dc sonoridad acústica
Por todo lo antes dicho es evidente la
dificultad que surge al tomar el dB como unidad de sonoridad acústica ya que a
sonidos con igual nivel de intensidad, igual medida en decibeles, puede
corresponder distinta sonoridad acústica, y sonidos con distinto nivel de
intensidad, distinta medida en decibeles, pueden provocar sensaciones de igual
sonoridad acústica.
Por ello es necesario definir una nueva unidad
que mida lo que realmente percibe el oído. Es decir mientras el dB es la unidad
de medida de una propiedad objetiva del sonido, su nivel de intensidad, la
nueva unidad debe estar referida a una propiedad subjetiva de la sensación
sonora, su sonoridad.
Con la ayuda de oyentes se determinan sonidos de
distintas frecuencias que son percibidos con la misma sonoridad acústica. Esto
permite determinar contornos prácticamente paralelos al umbral de audición que
constituyen niveles de sonoridad acústica y que unen puntos que representan
sonidos que producen sensaciones de igual sonoridad.
Se toma como unidad de sonoridad al fon de tal
forma que el nivel de sonoridad acústica de un sonido medido en fones es
equivalente al nivel de intensidad medido en decibeles de un sonido de 1000 Hz
que tiene la misma sonoridad.
De esta forma es posible construir los contornos
de la Fig. 3 que sobre 1.000 Hz toman la altura de 0, 10, 20, 30, 40, 50, 60,
70, 80, 90, 100, 110, y 120 dB y representan las curvas de nivel de sonoridad
de 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, ll0, y 120 fones.
Estas líneas también llamadas curvas isofónicas
representan sonidos de distinta frecuencia y nivel de intensidad (propiedades
objetivas) pero de igual sonoridad acústica (propiedad subjetiva).
A partir de la definición del fon puede
observarse que no es posible establecer una relación directa entre el número de
fones y la sonoridad con que se percibe un sonido.
Es decir; si bien mediante la definición del fon
se han podido determinar niveles de sonoridad y es posible afirmar que un
sonido de 40 fones es percibido con mayor sonoridad acústica que uno de 20
fones, no es posible asegurar que el primero sea percibido con el doble de
sonoridad que el segundo.
Para poder comparar dos sonidos se define el son
que corresponde a la sonoridad con que el oído normal percibe un sonido de
1.000Hz y 40dB de nivel de intensidad. Este sonido se toma como referencia para
determinar la sonoridad de cualquier otro sonido. De este modo un sonido que
posee el doble de sones que otro es percibido con el doble de sonoridad
acústica.
Si bien todos los sonidos ubicados sobre la
curva isofónica correspondiente a 40 fones tendrán una sonoridad de 1 son, no
existe una relación directa entre ambas unidades.
Nivel de
intensidad, dB
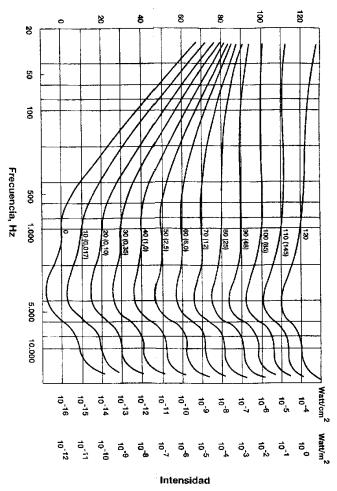
Fig 3 Curvas isofónicas en
el campo audible normal
La Fig. 4 establece la relación entre el nivel
de sonoridad medido en sones y la sonoridad medida en milisones.
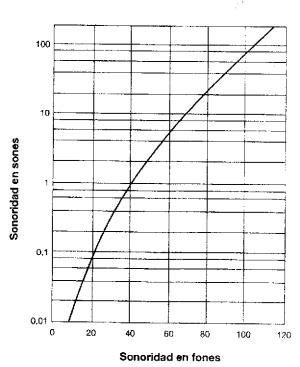
Fig. 4. Equivalencia en sones del nivel de sonoridad medido en
fones
El valor entre paréntesis en cada curva
isofónica de la Fig. 3 representa la sonoridad medida en sones.
1c. Enmascarado del sonido
La determinación del umbral de audición de un
tono puro requiere que el mismo sea percibido en el más perfecto silencio.
La presencia simultánea de otro sonido
interfiere la percepción del tono que se desea escuchar, situación que se
traduce en una elevación del umbral de audición para dicho tono.
Este fenómeno se denomina enmascarado o
enmascaramiento. El grado de enmascarado se mide por el aumento del umbral de
audición medido en unidades de nivel de intensidad. Si el grado de enmascarado
de un sonido es de 10 dB implica que debido a la presencia de otro sonido
enmascarador es necesario elevar la intensidad del sonido en 10 dB por encima
del umbral de audición para que sea apenas percibido
El grado de interferencia que se produce por la
presencia de dos sonidos simultáneos depende de las características físicas
tanto del estímulo acústico enmascarado como del sonido enmascarador. En
general depende de la intensidad y de la frecuencia del sonido enmascarador.
El enmascaramiento que produce un tono puro
sobre otro tono puro tiene características completamente distintas al
enmascaramiento producido por un ruido sobre un tono puro.
Se observa que para que un ruido enmascare un
tono puro es necesario que la banda del ruido tenga un ancho mínimo, banda
crítica, y que contenga la frecuencia del tono a enmascarar.
Experimentalmente se comprueba que el ancho de
la banda crítica es de aproximadamente un tercio de octava y que a medida que
aumenta la intensidad del ruido mayor es el número de frecuencias que
enmascara.
La Fig. 5 muestra la elevación del umbral de
audición producida por un ruido cuyo centro de banda está alrededor de 1.200 Hz
y su nivel de intensidad varía de 20 dB a 110 dB. Se observa que las
frecuencias altas son las más afectadas a medida que aumenta el nivel de
intensidad del ruido enmascarador.
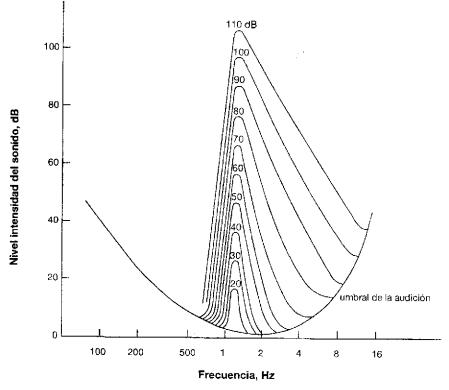
Fig. 5. Elevación del umbral de audición producido por un ruido de
1.200 Hz de centro de banda y para distintos valores de nivel de intensidad
Cuando el enmascaramiento es producido por un
tono puro se presentan dos situaciones. En la primera ambos tonos son de
frecuencia cercanas y en la segunda la interferencia se produce entre tonos
graves y agudos.
En el primer caso se observa que el grado de
enmascaramiento crece con la proximidad de ambos tonos. Es decir un tono dc
2.200 Hz enmascara mucho más a un tono de 2.300 Hz que otro de 1.500 Hz.
En el segundo caso la experiencia muestra que
sonidos de baja frecuencia, sonidos graves, son en general más efectivos para
enmascarar sonidos de alta frecuencia, sonidos agudos.
Cuando el enmascaramiento es producido por un
ruido cuyo ancho de banda es menor que el ancho de banda critico el efecto es
similar al enmascaramiento producido por un tono puro cuya frecuencia es igual
a la frecuencia central de la banda de ruido.
El menor número de voces masculinas frente a un
mayor número de voces femeninas en los coros es debido a la mayor capacidad de
enmascaramiento de los tonos graves sobre los tonos agudos.
La interferencia entre tonos puros de
frecuencias muy parecidas produce otro tipo de efectos como por ejemplo
batidos, que consiste en un sonido de frecuencia intermedia que presenta
variaciones periódicas en la sonoridad
1d. Fatiga auditiva
Como hemos visto el fenómeno de enmascaramiento
produce una elevación en el umbral de audición de un tono particular debido a
la presencia simultanea de otro tono o ruido.
No es el único caso en que se produce esta
elevación del umbral de audición. La experiencia muestra que también se produce
un fenómeno similar cuando el oído intenta percibir un tono después de haber
sido sometido a una estimulación acústica continuada.
Comúnmente se denomina a este fenómeno
aturdimiento o fatiga, y también es conocido como postenmascararniento,
enmascaramiento residual, adaptación o pérdida temporaria de la audición.
El nivel o cantidad de fatiga, al igual que el
enmascaramiento, se mide en decibeles y su valor equivale a la diferencia en el
umbral de audición al percibir un mismo tono antes y después de recibir una
estimulación acústica previa.
El nivel de fatiga depende de la intensidad y
duración del tono fatigante.
El grado de fatiga se mide en función del tiempo
transcurrido desde el momento en que se aplicó el tono fatigante.
Se observa que para sonidos fatigantes intensos
la fatiga aumenta en forma directa con la duración del estímulo previo. No
ocurre lo mismo para sonidos fatigantes débiles donde la fatiga no cambia a
pesar de que se incremente de 0,1 seg a 5 seg la duración del estímulo previo.
La Fig. 6 muestra la pérdida auditiva en función
del tiempo luego de aplicar como estímulo fatigante un ruido blanco de 115 dB
durante 20 minutos.
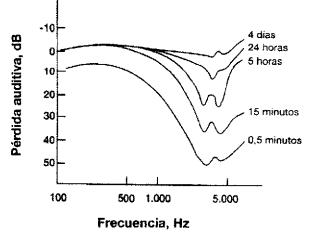
Fig. 6. Pérdida auditiva producida por un ruido blanco de 115 dB
aplicado durante 20 minutos
En general a bajas intensidades, la fatiga se
traduce en una elevación del umbral de audición en la zona de frecuencias
similares o muy cercanas a la del tono fatigante.
A medida que la intensidad del tono fatigante
aumenta la elevación del umbral de audición se va extendiendo hacia las
frecuencias mas altas.
La fatiga puede llegar a ser permanente como
producto de la exposición a ruidos o tonos muy intensos y durante tiempos
prolongados. Este fenómeno se denomina trauma acústico.
2a Percepción de la frecuencia
Cuando hablamos de sonidos graves o agudos
estamos haciendo referencia a una característica de la sensación sonora que
está relacionada con su tono o altura tonal.
El tono es una propiedad subjetiva que está
relacionada con la frecuencia del estímulo sonoro.
Si bien es cierto que a medida que aumenta la
frecuencia, propiedad objetiva, también aumenta el tono, propiedad subjetiva,
no existe una relación lineal directa entre ambas propiedades. Es decir, no es
cierto que si se duplica la frecuencia del estímulo sonoro se duplique la altura
tonal o el tono de la sensación percibida.
Al no existir una relación directa entre tono y
frecuencia, no es posible adoptar el Hz como unidad de tono.
Es necesario definir una unidad de medida de la
altura tonal y establecer la relación entre tono y frecuencia.
En 1.940 Vollanan y Stevens elaboraron una
escala de altura tonal. Para ello solicitaron a un conjunto de individuos que
ajustaran la frecuencia de un sonido hasta que su tono fuera percibido primero
como la mitad y luego como el doble del tono de otro sonido de referencia.
Luego solicitaron a los oyentes que construyeran
una escala de frecuencias en intervalos iguales de altura tonal.
Sobre la base de estos resultados se construyó
una escala de altura tonal que toma como unidad al mel, haciendo corresponder
una altura tonal de 1.000 meles a un sonido de 1.000 Hz y de 40dB.
Esta escala va de 1 a 3.500 meles y la relación
entre la frecuencia de una onda sonora y la altura tonal o tono de la sensación
se muestra en la Fig. 7.
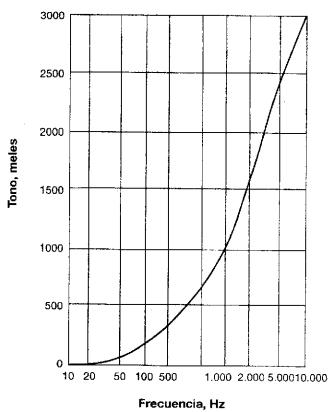
Fig. 7. Equivalencia entre las unidades de tono medido en meles y
las de frecuencia medida en Hz
2b Tono y sonoridad
Como ya se adelantó en la primera parte, el
aumento de la intensidad de la señal sonora incrementa el nivel del estímulo
sin provocar un desplazamiento de la zona excitada pero la amplía
comprometiendo un mayor número de fibras nerviosas próximas. Esto se traduce en
cambios en el tono de la sensación y pone de manifiesto que tono y sonoridad no
son características independientes.
La experiencia muestra que sonidos graves, con
menos de 1.000 Hz, son percibidos con una disminución de su altura tonal cuando
aumenta su intensidad. A su vez sonidos agudos, con más de 1.000 Hz, son
percibidos con un incremento de su altura tonal cuando aumenta la intensidad.
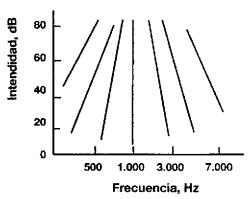
Fig 8. Rectas isotónicas
Todos los sonidos ubicados sobre cada línea de
la Fig. 8 son percibidos con la misma altura tonal. Cada línea de la figura se
denomina recta isotónica.
Los sonidos próximos a 1.000 Hz no experimentan
un cambio notable en su altura tonal con el aumento de la intensidad. Esta
propiedad de los sonidos de frecuencia intermedia de mantener su altura tonal
frente a los cambios de la intensidad ha motivado que se tome el tono de 1.000
Hz como patrón para muchas experiencias psicofísicas.
2c Agudeza tonal
Se llama agudeza tonal a la capacidad que tiene
el oído humano para detectar un cambio en el tono del sonido que percibe.
La experiencia indica que es más fácil detectar
cambios en el tono en los sonidos de alta frecuencia (tonos agudos) y resulta
más dificultoso para frecuencias bajas (sonidos graves).
El umbral diferencial para la altura tonal,
definido como la mínima variación de la frecuencia que es detectada como un
cambio en el tono, varía con la frecuencia y va de 2 a 4 Hz para sonidos de
menos de 2.200 Hz a más de 40Hz para sonidos de más de 10.000Hz.
La Fig. 9 muestra la variación del umbral
diferencial en función de la frecuencia.
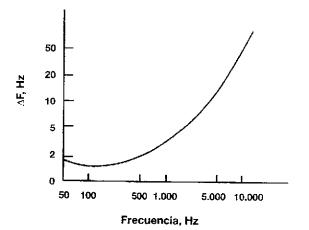
Fig. 9 Variación con la frecuencia del umbral diferencial de
altura tonal
Existen individuos capaces de reconocer un tono
sin necesidad de contar con otro tono de referencia. Se dice que estos
individuos poseen tono absoluto.
Esta variación en la agudeza tonal en función de
la frecuencia hace que una buena entonación sea mas difícil para tonos agudos
que para tonos graves debido a que el oído es más crítico para las altas
frecuencias.
2d Tono psicológico
Se denominan tonos subjetivos aquellos que son
percibidos aún cuando no están presentes en el estímulo sonoro externo.
Cuando se escuchan simultáneamente dos tonos
puros de frecuencias F1 y F2 y si F2 supera en más de 10 Hz a F1, se
percibe también otro sonido cuyo tono corresponde a una frecuencia igual a la
diferencia F2 - F1
Este es el motivo por el cual, si al oído llega
una señal sonora constituida por una serie de sobretonos, también se percibe el
tono fundamental correspondiente a dicha serie. Por ejemplo si el estimulo está
compuesto por sonidos de 200, 300 y 400 Hz también se percibirá el tono
correspondiente a 100 Hz aunque el mismo no esté efectivamente presente.
Si la separación entre F1 y F2 disminuye
por debajo de 10 Hz se percibe un sólo sonido cuya sonoridad varía
periódicamente con una frecuencia F2-F1, fenómeno que
comúnmente se llama pulsación. La Fig. 10 muestra este fenómeno para dos tonos
puros de 100 Hz y 105 Hz.
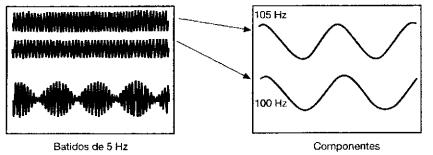
Fig. 10 Pulsaciones de 5 Hz producida por la superposición de dos
tonos de 100Hz y 105Hz
3a Timbre o calidad del sonido
La mayor parte de los sonidos que normalmente
llegan al oído no están constituidos por tonos puros. En general son sonidos
complejos estables o casi estables y ruidos.
En muchos casos, sobre todo en sonidos que
provienen de instrumentos musicales o inclusive correspondientes a la voz
humana, el estímulo sonoro esta compuesto por un modo fundamental acompañado
por una superposición de sobretonos o armónicos.
La sensación sonora posee la altura tonal
correspondiente a la frecuencia del tono fundamental pero va acompañada de
otras sensaciones que constituyen la calidad o el timbre del sonido complejo.
Esto hace que, si se produce una melodía
mediante el uso de dos instrumentos que aparentemente son iguales, por ejemplo
dos violines, se perciba que las características del sonido cambian de
instrumento a instrumento.
Es decir a pesar de que son prácticamente iguales,
y producen con igual sonoridad el sonido correspondiente a una misma nota,
existe una diferencia perceptible entre ambos.
Esto es mucho más notable en el sonido producido
por dos tubos de las mismas dimensiones pero de distinto material, por ejemplo uno
de madera y otro de metal. Si bien ambos físicamente deben producir sonidos
correspondientes a los mismos modos de vibración, la sensación sonora que
producen es diferente. Comúnmente se expresa diciendo que el tubo de madera
emite un sonido más "dulce", mientras que el de metal es más ”frío
o metálico".
Esta propiedad subjetiva de la sensación sonora
está relacionada con una propiedad objetiva del estímulo sonoro: la composición
espectral del sonido complejo.
La diferencia radica en el número de tonos y
sobretonos que están presentes en cada sonido y en la amplitud relativa de los
mismos.
En otras palabras la diferencia que se percibe
se debe a que los sonidos tienen distinto espectro.
En el ejemplo de los tubos, tenemos que, aunque
en ambos sonidos están presente los tonos correspondientes a los modos de
vibración de dos columnas similares de aire, la forma en que resuenan los tubos
de distinto material no es la misma. Luego existe una diferencia detectable
entre las amplitudes de los mismos tonos emitidos por cada diferente tubo.
En general, un emisor de sonido (instrumento
musical o el aparato fonador) está compuesto por un sistema productor de sonido
(cuerdas, columna de aire, membrana, cuerda vocal, etc) y un sistema de
resonancia (caja, tubo, tracto vocal, etc).
El sistema productor vibra según modos
permitidos generando un sonido complejo producto de la superposición según un
espectro original de un tono fundamental y los armónicos asociados a dicho
tono.
El sistema de resonancia vibra amplificando el
sonido proveniente del sistema emisor modificando el espectro original según su
propia curva de resonancia. Esto produce un sonido final cuyo espectro es el
resultado del efecto de los dos sistemas.
La Fig. 11 esquematiza la situación de dos
emisores de sonido que tienen igual sistema productor de sonido. El espectro
original común se ve afectado en cada caso según la curva de resonancia de cada
instrumento lo que origina dos sonidos de distinto timbre o calidad.
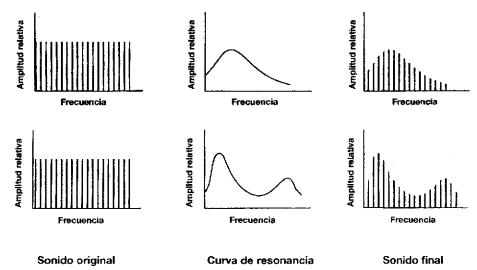
Fig. 11 a) espectro
original b) curvas de resonancia y c) espectros finales de dos instrumentos
Algo similar ocurre en el caso de la voz humana.
El sonido originado en las cuerdas vocales (sistema emisor) se transforma a lo
largo del tracto vocal (sistema resonador) que produce un espectro personal lo
que distingue el timbre de la voz de cada individuo particular.
La Fig. 12 muestra el espectro de dos sonidos
estables complejos que resultan de la superposición del mismo tono fundamental
F0 y la misma serie de armónicos pero que difieren en las amplitudes
de sus componentes.
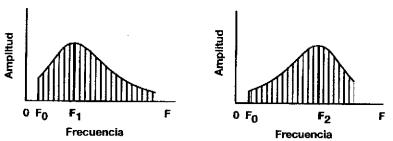
Fig. 12 Espectros de dos sonidos que tienen el mismo tono
fundamental pero que difieren en la amplitud relativa de los armónicos que los
componen
Ambas distribuciones espectrales presentan un
máximo para un valor particular de la frecuencia.
Debido a que el máximo en el primer sonido está
en una frecuencia F1 menor que la del máximo del segundo sonido F2,
será percibido con una sensación más grave.
Esta altura tonal del sonido complejo se llama
altura formática y la curva envolvente espectral se llama formante.
Si bien a partir del espectro de un sonido
complejo puede suponerse que estamos frente a una superposición de ondas
sinusoidales estables en el tiempo, debe tenerse en cuenta que en todo sonido
real tiene un principio, transitoria de ataque, y un fin, transitoria de
extinción, que no son exactamente sinusoidales. Más aún hay casos donde el
sonido es casi totalmente transitorias, por ejemplo en los sonidos que
provienen de instrumentos de percusión.
Sin embargo, la experiencia demuestra que en
todos los casos, aún en sonidos con gran presencia de transitorias, es posible
percibir un timbre característico.
Más aún, todo indica que las transitorias
constituyen una parte esencial para la identificación de un sonido. Un ejemplo
de ello es la dificultad que tiene el oído para identificar un sonido grabado
en el cual se han suprimido el principio y el final. Una situación parecida se
presenta cuando se invierte el sentido de reproducción de una cinta grabada,
aún cuando no se modifica esencialmente el espectro del sonido complejo grabado
es percibido con el timbre modificado.
Esto ha llevado a asociar al timbre, más que con
un espectro invariante, con la idea de un espectro que evoluciona
temporalmente.
Esta idea, si bien exige un análisis mucho mas
complejo, está más de acuerdo con lo que ocurre con los sonidos reales donde
cobra importancia no sólo la presencia y la duración de las transitorias sino
también la forma en que aparecen, desaparecen y evolucionan temporalmente los distintos
armónicos.
Esta forma más completa de interpretar las
propiedades objetivas de un sonido complejo, permite explicar las diferencias
que se perciben en el timbre de un sonido que proviene de un instrumento por
cambios de ejecutante, por las técnicas de ejecución, por la acústica de la
sala, por la técnica y la calidad de grabación, etc.
No obstante, más allá de las innumerables causas
de distorsión del timbre de un sonido, existen una serie de elementos que
constituyen los aspectos invariables que permiten identificar el instrumento y
las características básicas del sonido que emite.
Esto es lo que permite que, a pesar de las
diferencias que existen en el timbre de la voz de distintas personas, pueda
identificarse claramente cual es la vocal que están pronunciando.
3b Timbre y sonoridad
Experimentalmente se comprueba que el timbre de
un sonido complejo es muy sensible a los cambios de la sonoridad.
Un sonido complejo es la resultante de la
superposición de una serie de tonos puros de acuerdo con una dada distribución
espectral. Cada uno de estos tonos puros posee una frecuencia y una intensidad
determinada que determinan la sonoridad y la altura tonal de la sensación que
cada uno por separado produce.
Una variación en la sonoridad del sonido
complejo implica una variación en la sonoridad de cada uno de los tonos puros
que lo componen.
Sin embargo, el aumento o la disminución de la
sonoridad del sonido complejo no se traduce en una variación equivalente de
cada uno de los tonos que lo componen.
Más aún, puede ocurrir que con un aumento de la
sonoridad aparezcan como audibles tonos puros que conformaban el sonido
complejo pero estaban por debajo del nivel de audición o, si disminuye la
sonoridad, desaparezcan algunos tonos puros que antes eran audibles.
Por otro lado, un cambio de sonoridad hace
variar la altura tonal con que se percibe cada uno de los tonos puros que
componen el sonido complejo.
Estos cambios de altura tonal y amplitud
relativa de los tonos puros motivados por variaciones en la sonoridad implican
una nueva distribución espectral en la sensación sonora global dando lugar a
cambios en el timbre o calidad de dicha sensación.
La Fig. 13 muestra cómo variaciones en la
intensidad de un sonido complejo se reflejan en cambios en las características
de la sensación sonora.
En los tres casos el sonido complejo presenta un
espectro uniforme para los tres tonos puros de 80 dB en a), 20 dB en b) y 5 dB
en e), sin embargo la sensación sonora no refleja esta uniformidad.
Mientras en el caso a) la sensación es producto
de la percepción simultánea de tres tonos puros dos de los cuales, 200 Hz y
10.000 Hz, tienen la misma sonoridad y el tercero, 1.000 Hz, es percibido con
un 25 % más de sonoridad que los anteriores, en el caso b) la sensación es el
resultado de la percepción de sólo dos tonos puros uno de los cuales es más de
cinco veces más sonoro que el otro. En el caso c) lo que se percibe es un tono
puro de 1.000Hz.
Este ejemplo pone de manifiesto los cambios en
el timbre con el que se percibe la sensación sonora debido a variaciones en su
nivel de intensidad.
A los efectos de simplificar el ejemplo no se ha
tenido en cuenta la variación en la altura tonal de cada componente debida al
cambio en la sonoridad. Mientras el sonido de 1000 Hz no sufre cambios en su
altura tonal debido a la variación de su nivel de intensidad, el sonido de 200
Hz es percibido más grave y el sonido de1000 Hz es percibido más agudo cuando
aumentan en sonoridad. Este fenómeno es otra causa de cambios en el timbre de
la sensación sonora que debe sumarse a lo analizado en el ejemplo.
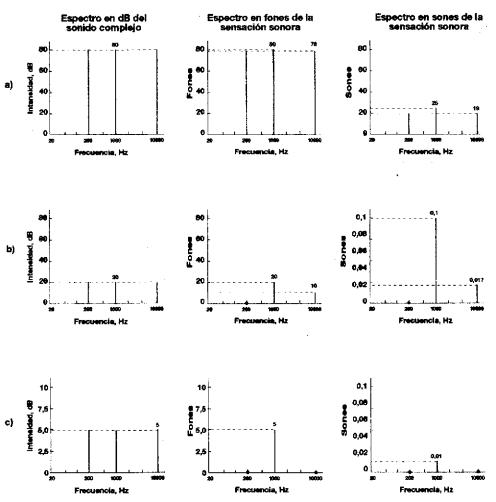
Fig. 13 Espectros de un sonido complejo en dB y de la
sensación producida medida en fones y sones para distintos niveles de
intensidad a) 80 dB, b) 20 dB y c) 5 db.
En la actualidad se han desarrollado instrumentos
electrónicos capaces de descomponer un sonido complejo en los tonos puros que
lo componen. Estos instrumentos, llamados analizadores, permiten determinar la
frecuencia y la intensidad de los tonos que conforman el espectro del sonido
complejo que es analizado.
A la inversa, también es posible en la
actualidad reproducir un sonido complejo si se conoce el espectro de los tonos
puros que lo componen. A partir del desarrollo de osciladores electrónicos
capaces de producir tonos puros de cualquier frecuencia, es posible sintetizar
un sonido complejo mediante la superposición de sonidos cuya frecuencia e
intensidad ajustan un espectro predeterminado. Estos instrumentos se conocen
como sintetizadores y se utilizan para reproducir los más variados sonidos
complejos, como por ejemplo los que provienen de instrumentos musicales e
inclusive los de la voz humana.
4. Percepción del volumen y la densidad
Como hemos visto, propiedades físicas del
estímulo sonoro (intensidad, frecuencia y espectro) tienen su correlato en
atributos característicos de la sensación sonora (nivel de intensidad, altura
tonal y espectro).
La relación entre las características física del
estímulo y los atributos de la sensación es por demás compleja existiendo una
notable interdependencia entre estos últimos.
Es común que cuando se describe la sensación
sonora se recurra a conceptos o categorías que se utilizan para describir otro
tipo de experiencias sensoriales. Así por ejemplo se dice que el timbre del
sonido de un instrumento de viento de madera es más "dulce" o más
"cálido" que el que proviene de un instrumento de metal. Se dirá que
este último es más "frío" o más “metálico”.
De la misma forma es común atribuir a la
sensación sonora otras propiedades como la de "penetrante",
"voluminosa", "densa", "compacta",
"difusa", etc. Propiedades comúnmente ligadas a cuerpos sólidos o a
nociones espaciales.
Después de muchos estudios Terrace y Stevens,
1.962 y Guirao y Stevens, 1.964 observaron que estas cualidades de la sensación
sonora estaban relacionadas con la intensidad y la frecuencia del sonido.
El volumen de un sonido es el atributo ligado a
una característica espacial que permite distinguir si la sensación sonora llena
más o menos el espacio.
Se ha medido esta característica en condiciones
de laboratorio y se ha determinado su unidad subjetiva, el vol.
De los resultados experimentales surge que los
sonidos graves aparecen como más voluminosos cuando se los compara con sonidos
agudos del mismo nivel de intensidad. Así mismo y para cualquier frecuencia se
percibe un aumento del volumen con el aumento del nivel de intensidad. Es
decir, un sonido de 200Hz y 60dB es percibido como más voluminoso que uno de
5.000 Hz y 60dB, y un sonido de 1.000Hz y 100dB es más voluminoso que uno de
1.000Hz y 20dB.
Mediciones experimentales efectuada por Terrace
y Stevens en 1962 sobre un número grande de oyentes permitieron determinar
curvas de igual volumen como las que se muestran en la Fig. 14.
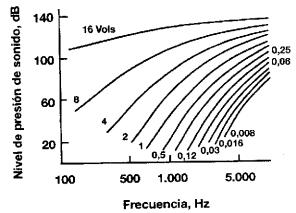
Fig. 14 Curvas de igual volumen en función de la frecuencia
De forma similar se ha determinado
experimentalmente la unidad subjetiva de la densidad de un sonido, el dens. Si
un sonido tiene más densidad que otro será percibido como más penetrante o
compacto. Se observa que a igual nivel de intensidad son más densos los sonidos
agudos que los graves y que a una frecuencia dada la densidad aumenta con la
intensidad del sonido.
Esto significa que un sonido de 2.000 Hz y 40 dB
es percibido como más denso que uno de 200 Hz y 40 dB mientras que un sonido de
1.000 Hz y 70dB es más denso que uno de la misma frecuencia pero de 30 dB.
Guirao y Stevens, 1.964, determinaron
experimentalmente y en condiciones de laboratorio las curvas de igual densidad
que se muestran en la Fig. 15.
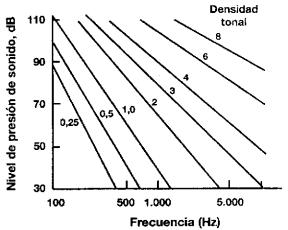
Fig. 15 Curvas de igual densidad en función de la frecuencia
Mezclando luces de color
Prof.
Fernando Fernández
(ferfeser@hotmail.com)
En un lugar cerrado y con posibilidad de
oscurecerlo por completo, montaremos sobre un tablero de madera tres focos de
luces dicroicas con portalámparas móviles con dos grados de libertad en sus
movimientos; una rotación en un plano horizontal y otra en un plano vertical.
Necesitaremos además de cables lo suficientemente largos para conectar las tres
lámparas en paralelo a un transformador de 220/12 volt; y será importante
contar con tres interruptores para comandar el encendido por separado de cada
una. Para conseguir las luces de colores emplearemos papel celofán en color
verde, azul y rojo; los cuales interpondremos sobre el haz de luz de cada
lámpara y así conseguiremos proyectar el color de luz deseada.
1ro. Empezaremos
por mezclar luces de a pares tratando de anticipar el color resultante y luego
confirmarlo.
Surgirá la idea de superponer a la vez luces de
color verde, azul y rojo. Evidentemente deberíamos obtener luz blanca pero es
posible que debamos esforzarnos con mucha voluntad para acordar que el color se
parece o tiende a ser blanca. Aquí es un buen momento para que nos preocupemos
de analizar las intensidades de cada lámpara (pues por más que el ferretero nos
diga que nos vendió tres lámparas iguales, nunca dos lámparas resultan ser
perfectamente idénticas), como también la calidad de los filtros empleados
(entiéndase por filtros, a los papeles de celofán).
2do. Es
interesante tomar un CD e interponerlo a el haz de luz "blanca" de
una de las lámparas y visualizar la descomposición de colores de la luz blanca.
A continuación podríamos interponer el CD al haz de luz roja y sacar
conclusiones acerca de la composición de esa luz.
Arriba hemos hecho referencia a la luz
proveniente de una de las lámparas desnudas (es decir sin celofán), como luz
blanca entre comillas; pues estas lámparas son de filamento incandescente y en
realidad emiten luz con alto componente de frecuencias que corresponden a el
amarillo y al anaranjado.
Explicación de la aparición de sombras curiosas
Trabajaremos a partir de ahora con sólo dos
lámparas y un objeto opaco a elección para interponer a los haces de luz
provenientes de cada lámpara. Podremos usar como pantalla una pared blanca y
deberemos colocar al objeto centrado según una línea que sea mediatriz del
segmento que une a las dos lámparas ( Ver figura 1).
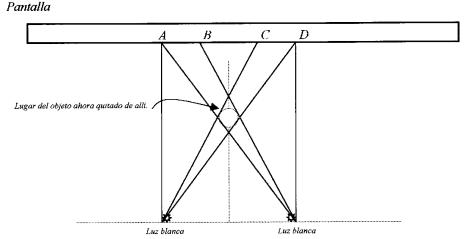
Figura 1-La figura muestra una vista
superior del montaje experimental
Sobre la pantalla hemos señalizado con letras
los segmentos delimitados por la llegada de rayos provenientes de ambas
lámparas.
Cada lámpara que vamos a considerar
perfectamente blanca aporta partes iguales de verde, azul y rojo. Diremos
entonces que a cada zona de la figura anterior llegan cantidades iguales de
azul, verde y roja. Más en detalle diremos:
Segmento
AB: (1R+ 1A + 1V)Lámpara izquierda + (1R+ 1A + 1V)Lámpara
derecha = 2R + 2A + 2V
Segmento
BC: (1R+ 1A + 1V)Lámpara izquierda + (1R+ 1A + 1V)Lámpara
derecha = 2R + 2A + 2V
Segmento
CD: (1R+ 1A + 1V)Lámpara izquierda + (1R+ 1A + 1V)Lámpara
derecha = 2R + 2A + 2V
Con 2R convendremos en indicar que llegan 2
unidades de color Rojo; con 2A que llegan 2 unidades de color azul y con 2V que
llegan 2 unidades de color verde.
Conclusión:
según nuestro modelo a todas los segmentos de pantalla llegan partes iguales de
los colores primarios y en consecuencia la pantalla se aprecia iluminada de luz
blanca en cada uno de sus segmentos con igual Intensidad
Ahora colocamos el objeto opaco en su lugar y
observamos la aparición de dos sombras en los segmentos AB y CD de la pantalla
y una zona central BC intensamente iluminada. Ver figura 2.
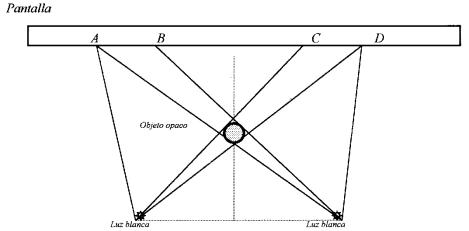
Figura
2
Las cantidades de luces que llegan por segmentos
se detallan a continuación:
Segmento
AB: (1R+ 1A + 1V)Lámpara izquierda + [(-1R) + (-1A) + (-1V)]Lámpara
derecha = 0R + 0A + 0V
Segmento
BC: (1R+ 1A + 1V)Lámpara izquierda + (1R+ 1A + 1V)Lámpara
derecha = 2R + 2A + 2V
Segmento
CD: [(-1R) + (-1A) + (-1V)]Lámpara izquierda + (1R+ 1A + 1V)Lámpara
derecha = 0R + 0A + 0V
Lo anterior muestra que a los segmentos AB y CD
llega luz blanca de intensidad cero es decir penumbra y que sobre el segmento
BC llega luz blanca de gran intensidad.
Con -1 se denota que esa luz no puede llegar a
ese segmento de pantalla pues no puede atravesar el objeto opaco.
A continuación repetiremos la experiencia pero
con luz blanca a la izquierda y luz roja a la derecha, producto de que se
interpone un filtro de color rojo (papel celofán) en el foco derecho. El filtro
de color rojo deja pasar luz roja pero absorbe luz verde y luz azul. A pesar de
que la intensidad de la luz decae luego de atravesar al filtro, consideraremos
que la intensidad de luz es igual a la de la luz blanca. Proyectando estas
luces sobre la pantalla con el objeto opaco interpuesto como en los arreglos
anteriores, se tiene que se forman dos sombras una de color intenso rojo y otra
de color cian. Ver figura 3.
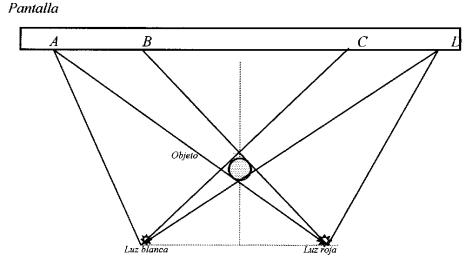
Figura
3
Las cantidades de luces que llegan por segmentos
se detallan a continuación:
Segmento
AB: (1R+ 1A + 1V)Lámpara izquierda + (-3R+ 0A + 0V)Lámpara
derecha = -2R + 1A + 1V
Segmento
BC: (1R+ 1A + 1V)Lámpara izquierda + (3R+ 0A + 0V)Lámpara
derecha = 4R + 1A + 1V
Segmento
CD: [(-1R) + (-1A) + (-1V)]Lámpara izquierda + (3R+ 0A + 0V)Lámpara
derecha = 2R + (-1)A + (-1)V
Lo anterior muestra que al segmento AB llega luz
cian( 1A + 1V) con deuda de rojo (-2R); sobre el segmento BC llega luz blanca
con alto contenido en rojo, diremos entonces que en ese segmento de pantalla el
color será blanco con tendencia al rojo y por último en el segmento CD llega
luz de color roja, con deuda de azul y verde. Tener en cuenta que el objeto
opaco quita luz al estar interpuesto. Por ello al interponerse al foco
derecho con luz roja quita 3 unidades de luz roja, mientras que al
interponerse al foco izquierdo de luz blanca quita 1 unidad de rojo, 1 unidad
de verde y 1 unidad de azul. Hemos considerado que la lámpara roja posee la
misma intensidad que la blanca y que la intensidad viene dada por las unidades
de color que tenga el haz de luz.
Por ello la lámpara izquierda (BLANCA) tiene
intensidad 3 = 1A + 1V + 1R y la derecha(ROJA) tiene también intensidad 3 = 0A
+ 0V + 3R.
Ejercicio:
Realizar los arreglos experimentales para iluminar al objeto opaco con
luz blanca y luz verde. Repetir pero ahora con luz blanca y luz azul.
Finalmente explicar los colores en las sombras a partir del modelo
presentado.
Es importante intercambiar las posiciones en
cada caso de las luces y tratar de predecir los resultados que arrojará la
experiencia
El Trompo
Lic. Auro Torres
El estudio de la dinámica de las rotaciones casi
siempre se reduce al caso de un cuerpo rígido que puede girar sobre si mismo
alrededor de un eje fijo respecto a un sistema de referencia inercial.
Se entiende por sistema de referencia inercial
uno en el que se cumplen las leyes de Newton
El caso de eje de rotación no fijo, en general,
se deja de lado, tal vez, por la dificultad, tanto en comprenderlo como en
explicarlo.
Para este caso un ejemplo que merece ser
estudiado y no ignorado es el trompo, elemento muy familiar para los alumnos y
cuya cinemática y dinámica es muy similar a muchas aplicaciones tecnológicas.
El ejemplo del trompo se hace interesante cuando se introduce la precesión y es
lo que se analizará en este artículo.
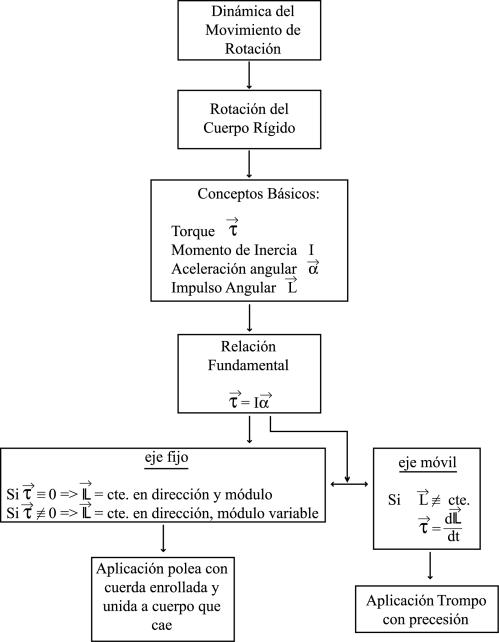
El esquema conceptual adjunto se presenta como
una base para otro diseñado a gusto del Profesor para que le sea mostrado a los
alumnos y vean de que modo intervienen las variables significativas en las
rotaciones, según que el eje sea fijo ó no.
En la FIG. 1 se muestra un trompo que gira
alrededor de su eje de simetría con velocidad angular w constante y manteniendo la punta del trompo fijo en el origen P
de un sistema de referencia inercial.. El movimiento en el cual el eje del
trompo, el cual gira rápidamente, rota alrededor del eje vertical describiendo
un cono se llama precesión. Veremos ahora como es posible predecirlo
partiendo de los principios de la mecánica clásica, y en particular
calcularemos wp que es la velocidad angular del movimiento de precesión.
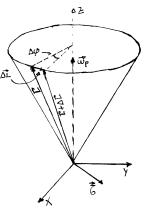
Figura 1
En el instante mostrado en la Fig. 2, el trompo
tiene una velocidad angular w
alrededor de su eje. También tiene un impulso angular L alrededor de ese
mismo eje, y este último forma un ángulo q con la vertical.
Sobre el trompo actúan dos fuerzas: una dirigida
hacia arriba, sobre el pivote en P, no representada en la figura, y la fuerza
de atracción de la gravedad o peso, que actúa hacia abajo en el centro de masa
del trompo. La fuerza hacia arriba a través de P no ejerce torque pues su brazo
de palanca es nulo. Por su parte, el peso m . g ejerce un torque,
respecto de P, dado vectorialmente por la ecuación
t = r x F = r x m . g
en donde r localiza el centro de masas
respecto del pivote P. El vector t es
perpendicular al plano formado por r y m . g y, al igual que r
y L, gira alrededor del eje z con una velocidad angular wp conforme el trompo precesa.
Cuando sobre un cuerpo rígido actúa un torque,
su impulso angular cambia según la relación fundamental
t = dL / dt
Como L es un vector puede cambiar su
magnitud como así también, su dirección y sentido.
Esta ecuación demuestra que el cambio en L
(dL) debe apuntar en la dirección de t. En la FIG. 1 t es
perpendicular a L; por lo tanto, dL producido por el torque,
también debe ser perpendicular a L.
Explicación cualitativa de la precesión
Observemos el movimiento del -trompo durante un
tiempo Dt (muy pequeño). En este intervalo la ecuación anterior predice un
cambio del impulso angular dado por
DL = t . Dt (1)
En la Fig. 1 se muestra el cambio DL, que al igual que t es perpendicular a L, y en ella
se observa el cono descripto por la precesión del eje del trompo, omitiendo a
este para mayor claridad.
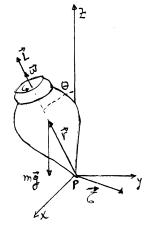
Figura 2
El impulso angular del trompo al final del
intervalo de tiempo Dt es la suma vectorial de L y DL. Como estos son perpendiculares entre si, y como DL << L, el nuevo vector de impulso angular L + DL tendrá la misma
magnitud que L, pero tendrá una dirección diferente. Por lo que el
-extremo del vector impulso angular se moverá en un circulo horizontal a medida
que transcurre el tiempo, ver Fig.1. Debido a que este vector se encuentra a lo
largo del eje de rotación del trompo, lo dicho constituye una explicación
cualitativa del movimiento de precesión del trompo.
Cálculo de la velocidad angular de precesión
La velocidad angular de precesión wp se puede obtener desde la Fig.1, en la que
wp = Dj / Dt
Pero como DL << L, tenernos
desde la Ec.(1) que
Dj @ DL / L . sen q = t Dt / L . sen q
entonces:
wp = Dj / Dt = t / L . sen q (2a)
Como además, ver Fig. 2
t = r m g sen(180 - q) = r m g sen q
obtenemos por último
wp = m g r / L. (2b)
Debe notarse que la velocidad angular de
precesión es independiente de q e inversamente
proporcional a la magnitud del impulso angular. Si este último es grande la
velocidad angular de precesión será pequeña. Como L es proporcional a w,
a mayor w menor wp.
La Ec.(2b) puede expresarse en forma vectorial.
Reescribiendo la Ec.(2 a) como
t = wp L sen q
la cual es una versión escalar de la relación
vectorial
t = wp x L
Esta es la expresión vectorial general que
relaciona la velocidad angular de precesión con el torque y el impulso angular.
El producto vectorial t = wp x L determina la dirección y magnitud correcta de t.
Introducción a la Dinámica
Notas
para el alumno
Lic.
Carlos Magallanes
1 Introducción
En la Unidad de cinemática se estudió el
movimiento de los cuerpos. Allí aprendimos cómo describir gráfica y
analíticamente un movimiento, en especial el movimiento rectilíneo uniforme y
el uniformente variado.
En esta Unidad analizaremos también el movimiento
o cambio de movimiento de los cuerpos, pero procurando encontrar una relación
entre dicho movimiento o cambio de movimiento y la causa que lo produce.
El nombre de esta Unidad se explica porque la
parte de la Física que estudia las causas de los movimientos es la dinámica.
La cuestión respecto al porqué se mueven los
cuerpos surgió en la mente humana hace 2500 años, pero recién en la época de
Galileo y Newton (1600) se encontraron respuestas que aun hoy perduran. Dicha
respuesta se encuentra en las Leyes de Newton de la dinámica, lo cual es el
tema principal de esta Unidad.
2 Principio de Inercia - Galileo:
¿Qué es necesario hacer para que un cuerpo se
mueva? Ejemplos: qué debo hacer para:
1. cambiar de lugar un banco en el aula?
2. levantar un cuerpo?
3. hacer llegar una piedra a cierta distancia?
4. hacer girar un trompo?
¿Qué es necesario hacer para que un cuerpo
cambie de dirección en su movimiento? Ejemplos: qué debo hacer para:
a) detener un cuerpo que está cayendo?
b) devolver una pelota en un partido de tenis?
c) pasar la pelota a un compañero en un partido de fútbol?
d) que mi automóvil tome una curva?
e) que un automóvil se detenga?
Las preguntas anteriores se pueden contestar de
diversos modos, pero un análisis sencillo mostrará que en todas las respuestas
estará, dicho con un nombre u otro, lo que comúnmente llamamos fuerza.
Es decir ya sabemos por lo aprendido en la vida
diaria, que la causa de los movimientos o más generalmente hablando: los
cambios de movimiento se obtienen aplicando fuerzas.
Ahora bien: no podemos quedarnos con una
respuesta tan simple y que nos aporte tan poca información. Debemos buscar
leyes físicas de mayor amplitud que nos permitan, conocida la causa del
movimiento (la fuerza) predecir cual será el comportamiento (movimiento o
cambio de movimiento) del cuerpo.
El progreso de la dinámica hasta su forma actual
estuvo paralizado por la teoría Aristotélica, que imponía diferentes
naturalezas al movimiento de los cuerpos en la superficie terrestre y a los
movimientos celestes, recurriendo a diversas y complicadas explicaciones para
distintos movimientos. Fue Galileo (1600) quien dio el primer paso al obtener
una explicación sencilla para el movimiento, ya sea terrestre o celeste. Su
resultado fundamental es lo que se conoce como Principio de Inercia de Galileo,
que afirma, en términos similares, que si no se ejerce ninguna fuerza sobre un
cuerpo, éste permanecerá en reposo o se moverá con velocidad constante.
El modo como Galileo llegó a este Principio es
un brillante ejemplo de cómo la mente humana, a partir de evidencias
experimentales y razonamientos puede alcanzar resultados de amplia validez.
Galileo estudió los movimientos de diversos objetos sobre planos inclinados,
observando que cuando los planos son descendentes existe una causa de
aceleración, y que cuando son ascendentes hay una causa de retardamiento. De
esto, razonó que cuando no hay ascenso ni descenso no debe haber aceleración ni
retardamiento. Cuando Galileo experimentaba para hacer estos razonamientos
observó que los movimientos horizontales no eran permanentes, pero también
observó que a medida que pulía la superficie (o sea disminuía la fricción o
rozamiento) los cuerpos se movían durante más tiempo con velocidad constante.
De estas observaciones dedujo que la fricción era la que proporcionaba las
fuerzas que detenían los cuerpos en su movimiento horizontal y concluyó que en
ausencia de tales fuerzas el cuerpo continuaría moviéndose en línea recta
indefinidamente.

|
Pendiente
negativa
Movimiento
descendente
La
velocidad crece
|
|
Pendiente
positiva
Movimiento
ascendente
La
velocidad decrece
|

Pendiente nula
¿ Cambia la
velocidad?
Figura 1
Así estableció un resultado para una situación
idealizada donde no actúan fuerzas. En otras experiencias puso planos
inclinados como lo indica la figura 2.
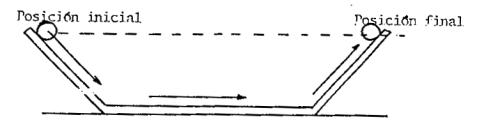
Figura 2
Al lanzar una esfera desde el punto A, ella
ascenderá por el otro plano hasta casi la misma altura. Galileo sabía que la
fricción impedía que alcanzara justamente la misma altura.
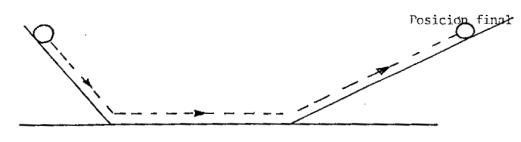
Figura 3
Si disminuía la pendiente del plano ascendente
la esfera tenía que recorrer más camino para alcanzar la altura inicial (fig.
3). Si dicha pendiente se reduce a cero el objeto se moverá eternamente
buscando alcanzar dicha altura (fig. 4).
Galileo concluía entonces “. . . el movimiento a lo largo de un plano horizontal es perpetuo. . .
” .

Figura 4
Observe cómo Galileo combinó resultados
experimentales con razonamientos para obtener un importante principio físico.
De este modo abrió el camino, luego seguido por Newton, al desarrollo de la
dinámica y a la manera de cómo utilizar experiencias sencillas e idealizadas
para obtener resultados que valen para movimientos mucho más complejos y en
mayores dimensiones que los mencionados aquí.
Galileo no estableció su principio de inercia en
base a la observación de un fenómeno aislado, muy por el contrario observó
numerosas situaciones físicas que le ayudaron a formularlo. El formulaba una
hipótesis, la sometía a prueba y para ello extraía deducciones de su hipótesis
que pudieran ser confrontadas con los experimentos. Si la prueba fallaba,
introducía una hipótesis diferente o modificaba la anterior a la luz de los
resultados del experimento y así continuaba con el proceso hasta obtener una
teoría que estuviera de acuerdo con todos los resultados experimentales.
Este método de trabajo: observación - hipótesis
- deducción de consecuencias de las hipótesis - experimentación - comparación
de predicciones y resultados experimentales - modificación de las hipótesis si
fuera necesario y así sucesivamente, introducido por Galileo a mediados del
siglo XVII, es la base del método que utiliza la ciencia actual, llamado Método
Científico. Por ello se lo puede considerar como el fundador de la Ciencia
Moderna.
La tecnología actual nos ofrece muchas
facilidades para hacer experimentos que a Galileo y Newton les exigieron mucho
tiempo, esfuerzo e imaginación. Por eso existe el peligro de no llegar a
comprender cabalmente la importancia de los trabajos de estos genios de la
Física. Dicho peligro se puede eliminar de un solo modo: estudiando la historia
de las ciencias desde la época de Aristóteles hasta nuestros días para
comprender el modo de pensar de los filósofos de la antigüedad y cómo fue
evolucionando el pensamiento científico.
Esto servirá también para comprender mejor otros
temas de física donde paso a paso se hace uso de estos resultados.
Este último comentario, además de advertir de la
importancia de los trabajos de Galileo, es una invitación a leer en la
bibliografía correspondiente la historia y evolución de la Física.
3 Primera Ley de Newton:
Cuando Newton empezó a estudiar e investigar en
ciencia heredó de Galileo un clima de desarrollo y propagación en la
investigación científica que supo aprovechar inteligentemente. En su obra
"Principios matemáticos de la filosofía natural" aparecida en 1657,
resumió y reordenó los conocimientos sobre dinámica existentes hasta ese
momento, enunció su ley de Gravitación Universal y sus tres leyes del
movimiento. Esta obra de Newton permitió definir con precisión conceptos
físicos que habían aparecido con Kepler y Galileo, y que hoy utilizamos con
mucha naturalidad: inercia y fuerza.
Entenderemos, de acuerdo con Newton, por inercia
la propiedad de la materia que se manifiesta en la tendencia de los cuerpos a
permanecer en reposo o en movimiento rectilíneo uniforme, o sea la resistencia
a los cambios de movimiento; por otro lado entenderemos por fuerza a la causa
de los cambios en el movimiento. Si no hay fuerza no hay cambio en el
movimiento.
Reconociendo Newton que el Principio de Inercia
de Galileo, es válido para todo cuerpo en todo punto del espacio y en cualquier
instante, incluyó dicho principio en su leyes del movimiento, es lo que se
conoce como “Primera Ley de Newton”:
"Todo cuerpo continuará en su estado de
reposo o en movimiento uniforme en línea recta, a menos que sea obligado a
cambiar este estado por fuerzas que actúen sobre él".
¿Es posible aislar absolutamente un cuerpo, en
movimiento ó en reposo, de toda fuerza?
Cuando un cuerpo se mueve existen fuerzas de
rozamiento que si bien es posible reducir en su influencia retardadora, es
imposible eliminar totalmente. Además, aún cuando el cuerpo está en reposo
actúan sobre él distintas fuerzas de distinto origen, ya sea por los cuerpos
que están próximos o que están en contacto con él. Es decir que solo idealmente
podemos tener un cuerpo libre de fuerzas.
¿De qué nos sirve el Principio de Inercia si es
imposible lograr la situación física para la cual vale?
La solución es sencilla: si bien no podemos
eliminar las fuerzas externas, podemos en cambio contrarrestarlas en sus
efectos, de tal modo que el efecto neto sea nulo. Por lo tanto si tenemos un
cuerpo en reposo o que se mueve con movimiento rectilíneo uniforme con
velocidad constante, ello significa que todas las fuerzas que actúan sobre él
están balanceadas o dicho de otro modo: la fuerza neta es nula. En este caso
decimos que las fuerzas se equilibran unas a otras.

Figura 5
Si el carrito no se mueve sobre la mesa
significa que la pesa P1 está equilibrada por la P2.
En el caso del carrito sobre la mesa, o
cualquier cuerpo apoyado, sabemos que si sacamos el apoyo el cuerpo cae. No es
que aparezca una fuerza cuando sacamos el apoyo. La fuerza está actuando
permanentemente y cuando el cuerpo se apoya, por ejemplo en una mesa, ésta al deformarse
ejerce un fuerza opuesta, de tal modo que la fuerza neta es nula. Al levantar
el cuerpo de la mesa, la deformación desaparece y por lo tanto la fuerza.
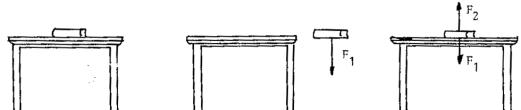
Figura 6
Para resumir entonces concluimos que:
a) El Principio de Inercia vale tanto en situaciones
ideales (cuerpo absolutamente libre de fuerzas) como también en situaciones
reales (si las fuerzas que actúan sobre el cuerpo lo hacen de tal modo que sus
efectos se contrarrestan totalmente).
b) Podemos explicar qué significa que un cuerpo
esté en reposo o se mueva con Movimiento Rectilíneo Uniforme: significa que
está en equilibrio pues no hay fuerza neta actuando sobre él.
c) Podemos predecir qué sucederá cuando sobre un
cuerpo actúan fuerzas que no se contrarrestan totalmente, o sea cuando la resultante
de las fuerzas no sea nula: si está en reposo comienza a moverse y si está en
movimiento uniforme y rectilíneo cambia su estado de movimiento: aumenta o
disminuye su velocidad, cambia la dirección del movimiento, o ambas cosas
simultáneamente.
En el siguiente punto analizaremos en detalle
esta predicción y sus resultados nos conducirán a la que se conoce como Segunda
Ley de Newton o Ley de Masa.
4 Concepto de Fuerza:
En el punto anterior concluimos que cuando sobre
un cuerpo actúan fuerzas no equilibradas cambiará su estado de movimiento.
Decir esto significa que varía su velocidad o su trayectoria o ambas cosas a la
vez. Para simplificar, por ahora, consideraremos el caso de que el cuerpo sólo
se mueve en línea recta, por lo tanto la acción de fuerzas no equilibradas
implicará cambio de velocidad, y si recordamos lo visto en la Unidad 1, un
cambio de velocidad significa decir que existe aceleración.
La Segunda Ley de Newton, o Ley Fundamental de
la Dinámica, establece la relación cuantitativa entre la fuerza neta que actúa
sobre un cuerpo y la aceleración que dicha fuerza le produce. Antes de analizar
dicha ley concentraremos la atención sobre lo que significa fuerza, dado que
estamos utilizando un concepto físico sin habernos detenido a meditar sobre su
significado.
Todos tenemos una idea intuitiva de lo que es
fuerza y la usamos en la vida diaria para distintas situaciones sin haber
estudiado previamente Física.
Por ejemplo, son frecuentes frases como:
a) "Juan es capaz de hacer más fuerza que Raul".
b) "No tengo suficiente fuerza para levantar esta valija".
c) "Me dolió porque me pegó con mucha fuerza"
Estos son ejemplos de fuerzas musculares y son
las más familiares porque las podemos sentir y ejercer. Pero ellas no son el
único tipo de fuerzas que existen. Un automóvil se puede mover ya sea
empujándolo con una fuerza muscular o con la fuerza de su motor; un objeto
pesado se puede levantar con el esfuerzo muscular o utilizando una grúa; un
clavo se puede mover porque se lo empuja con la mano o se lo atrae con un imán;
un cuerpo cae porque la Tierra lo atrae con una fuerza llamada peso; un cuerpo
cargado eléctricamente atrae o repele a otro también cargado con carga
eléctrica; un cuerpo se puede lanzar a cierta distancia empujado por la mano o
por un resorte comprimido.
En los ejemplos se ve que fuerzas de distinta
clase u origen pueden tener los mismos efectos cuando actúan sobre un mismo
cuerpo. Esto de paso pone en evidencia que resulta difícil dar aquí una
definición completa de fuerza ya que eso requeriría el estudio de otros temas
que están fuera de los objetivos y alcances de este curso.
Por eso evitaremos el dar una definición
rigurosa y seguiremos con nuestra idea inicial de fuerza como la causa de los
cambios de movimiento. Nos preocuparemos en cambio en analizar en detalle las
características de la fuerza.
Veamos distintas situaciones experimentales:
I) Suponga una mesa en
el centro del aula. Se le pide que le aplique una fuerza de origen muscular.
¿De cuántos modos lo puede hacer?. De muchísimos modos: por ejemplo tirando de
ella hacia Ud. , empujándola para que deslice, empujando o tirando hacia
izquierda o derecha, empujándola contra el piso, tratando de levantarla, etc.
Como Ud. ve, es necesario precisar hacia dónde
se debe aplicar la fuerza.
II) Suponga ahora que,
satisfaciendo su inquietud, se pide lo mismo pero con la aclaración de que
empuje en la dirección Norte-Sur.
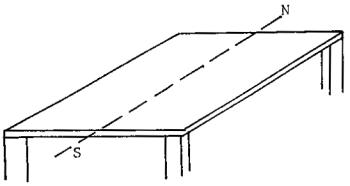
Figura 7
Ud. lo puede hacer de dos modos, o empujar hacia
el Norte o empujar hacia el sur. Como vemos, además de la dirección de la
fuerza, es necesario precisar el sentido de la fuerza. Finalmente queda por
notar que a la mesa puedo empujarla con mucha o poca fuerza. Resumiendo se
concluye que:
"para identificar plenamente una fuerza
debe especificarse cuál es su dirección, cuál es su sentido y cuál es su
intensidad".
Magnitudes físicas que requieren estas
condiciones para su identificación se denominan magnitudes vectoriales. Para
indicarlas se usa un vector junto con la letra, por ejemplo o.
Ejemplo:
|
Sobre el
carrito actúa una fuerza
horizontal hacia la derecha de
intensidad = 4 unidades.
|
Sobre la
cuerda actúan fuerzas
horizontales de sentido opuesto
y de igual magnitud.
|

Figura 8
Continuando nuestro análisis de concepto de
fuerza nos queda ahora por hablar de cómo se miden las fuerzas y en qué
unidades se miden. Aún no encararemos el tema de las unidades, pero si veremos
cómo hacer para, por lo menos, detectar cuando actúa una fuerza sobre un
cuerpo.
Consideremos un conjunto de cuerpos iguales, por
ejemplo esferas de plomo. Además un resorte colgado de un soporte.
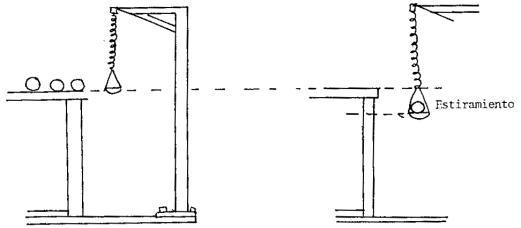
Figura 9
Si queremos sostener con la mano una de las
esferas debemos hacer una fuerza vertical hacia arriba, de una intensidad que
sea igual a la que el peso de la esfera hace hacia abajo.
Podemos hacer lo mismo colgando la esfera del
resorte. Veremos que éste se estira una cierta longitud hasta lograr sostener
la esfera. Es fácil deducir que el resorte al terminar de estirarse está
ejerciendo una fuerza, en este caso vertical y hacia arriba, de intensidad
igual a la que hacía la mano al sostener el cuerpo. En el laboratorio
verificaremos que al colgar dos esferas, el estiramiento es el doble que para
una, al colgar tres el estiramiento es el triple que para una, y así siguiendo.
En otras palabras:
"Cuando mediante una fuerza se estira un
resorte, el estiramiento es proporcional a la fuerza aplicada"
En símbolos:
X a F o
F = K . X (1)
k se conoce como constante del resorte y a (1)
como Ley de Hooke.
Esta propiedad de los resortes se puede utilizar
para medir fuerzas, tomando una fuerza como unidad. Sobre una escala se marca
el estiramiento producido por la fuerza unidad. Cuando se mide, por ejemplo,
una fuerza tres veces la unidad, el índice marcará un estiramiento triple y así
siguiendo. Este es el fundamento de los dinamómetros y volveremos a hablar de
ellos al final de la unidad.
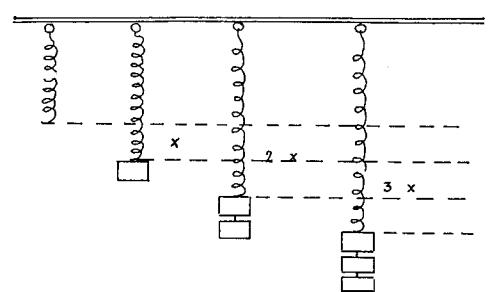
Figura 10
5 Segunda Ley de Newton
Vamos a deducir esta Ley a través de una
experiencia realizable en el Laboratorio.
Trabajaremos con el mismo dispositivo utilizado
en las prácticas de Cinemática (riel neumático).
Recuerde que allí verificamos que todo cuerpo,
libre de la acción de fuerzas, permanece en reposo o en movimiento uniforme y
que, bajo la acción de una fuerza constante, realiza un movimiento
uniformemente variado, o sea con aceleración constante.
Podemos preguntarnos, ahora, lo siguiente:
a) ¿De qué manera varía la aceleración que adquiere un cuerpo de masa
M cuando varia la fuerza aplicada sobre él?
b) ¿Qué aceleración adquieren cuerpos de distintas masas cuando se
aplica sobre ellos una misma fuerza?
Iremos por partes.
Para estudiar la relación entre la aceleración y
la fuerza aplicaremos al carrito distintas fuerzas. Como en nuestro dispositivo
experimental el rozamiento es despreciable, consideraremos como única fuerza
aplicada, la que ejerce la pesa, a través de la cinta, sobre el carrito.
Cuando aplicamos una fuerza F1 determinamos, del
mismo modo que en la Unidad I, una aceleración a1. Repetimos la
experiencia con fuerzas doble y triple y obtenemos a2 y a3.
O sea:
F1
à a1
F2 à a2
F3
à a3
etc.
¿Si F2 es el doble de F1,
cómo es a2 respecto de a1?
¿Si F3 es el triple de F3,
cómo es a3 respecto de a1?
En la práctica procederemos así
1. -Colgamos de la cinta la pesa 1 (5 gramos aproximadamente).
Determinamos la aceleración a1.
2. -Colgamos, ahora, una pesa 2 (10 gramos). Determinamos a2.
3. -Repetimos para 15 y 20 gramos y determinamos a3 y a4.
4. -Ordene en una Tabla los valores obtenidos y observe
cuidadosamente.
Observamos:
A fuerza doble
corresponde aceleración doble.
A fuerza triple
corresponde aceleración triple.
Etc.
Por lo tanto podemos afirmar, en forma general,
que la aceleración es directamente proporcional a la fuerza aplicada.
a a F
Podemos también encontrar esta proporcionalidad
construyendo la gráfica de aceleración versus fuerza.
Para analizar la variación de la aceleración con
la masa frente a una misma fuerza, realizamos la siguiente experiencia
Registraremos el movimiento del carrito para distintos valores de su masa, para
lo cual le agregaremos al mismo masas de distintos valores. En todos los casos
el peso suspendido del extremo de la cinta debe ser el mismo. Obtendremos lo
siguiente:
M1
à a1
M2 à a2
M3 à a3
¿Al aumentar la masa M del carro, la aceleración
aumenta o disminuye?
Para darnos cuenta de qué relación existe entre
la masa y la aceleración, hagamos el siguiente cálculo:
M2
/ M1 = a1
/ a2 =
M3 / M2 = a2
/ a3 =
Verificaremos que ambas proporciones son
iguales, entonces podemos afirmar que la aceleración adquirida por el carrito
es inversamente proporcional al valor de la masa del mismo.
a a (1 / M)
En la Primera Ley de Newton definimos la inercia como una propiedad natural de
los cuerpos a permanecer en reposo o en movimiento rectilíneo uniforme. Dado
que hemos experimentado con un carrito sobre el que actúa una fuerza,
apareciendo como consecuencia una aceleración, hemos obligado al carrito a
cambiar su estado, actuando en contra de su inercia. La mayor o menor inercia
del carrito se pondrá de manifiesto por la menor o mayor aceleración que
adquiera frente a la acción de una misma fuerza. Comprobamos experimentalmente
que la mayor o menor aceleración del carrito depende de su menor o mayor masa,
por lo cual podemos concluir que la masa es la responsable de la inercia del
carrito. A esta masa se la denomina masa inercial.
Podemos reunir las conclusiones obtenidas en una
sola:
a a (F / M)
En esta relación podemos sustituir el signo de
proporcionalidad por el de igualdad si multiplicamos por una constante, cuyo
valor depende del sistema de unidades utilizado. Si las unidades de F, M y a se
eligen apropiadamente la constante vale 1. Entonces:

 a = F / M o F = M . a
a = F / M o F = M . a
Esta última relación es conocida como Segunda
Ley de Newton de la Dinámica. Es aplicable a los fenómenos de la -vida diaria.
En un principio se aceptó su validez sin ningún tipo de restricción. Luego se
encontró que, cuando un cuerpo se mueve en las proximidades de la velocidad de
la luz, esta expresión necesita ser modificada por el hecho de que, en esas
circunstancias, la masa no es constante (física relativista). También se determinó
un limite en su validez cuando se trabaja en escalas atómicas. (Mecánica
cuántica).
Antes de continuar analicemos el siguiente
problema:
Dos masas M y m están unidas por medio de una
cuerda. M está sobre una mesa sin roce y m está suspendida libremente como
indica la figura 11.
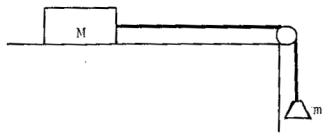
Figura 11
Este dispositivo representa el utilizado en la
experiencia de Laboratorio donde M es la masa del carro, m la masa de las pesas
y la mesa el riel neumático. Las fuerzas que actúan sobre M y m se indican en
los esquemas de la figura 12(a). F es la tensión en la cuerda y se
transmite a M a través de la misma. Mg es la atracción de la Tierra
sobre M y N es la fuerza ejercida sobre M por la mesa. El bloque M
acelerará en la dirección de las x solamente, de modo que ay
es igual a cero. Para M podemos plantear las siguientes relaciones:
N
- Mg = 0 (eje y) y F
= M ax (eje x)
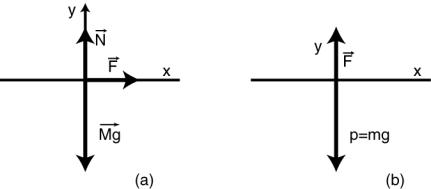
Figura 12
Para determinar F, debemos considerar el
movimiento de m. Las fuerzas que actúan sobre m se muestran en la Figura 12(b).
Como la cuerda y m están acelerando, no podemos concluir que F sea igual a mg.
Si F fuese igual a mg la fuerza resultante sobre m seria cero, condición que
sólo es válida si el sistema no está acelerado.
En nuestra experiencia de Laboratorio tomamos
como fuerza actuante sobre el carro P = mg, cuando, en realidad, tendríamos que
haber considerado F, cuyo valor desconocemos. Es posible salvar esta
dificultad, si consideramos que P = mg es la fuerza que actúa sobre el sistema
carro-pesas (M + m). Sistema carro-pesas conforman ahora, el cuerpo en estudio.
Para variar la fuerza aplicada, manteniendo la masa del sistema constante,
procedemos así supongamos que la suma total de pesas a utilizar sea 20 gramos.
Cuando suspendamos 5 gramos, los 15 restantes se agregarán al carro. Si
suspendemos 10 gramos, los restantes 10 se colocarán en el carro, de manera tal
que los 20 gramos siempre formen parte de la masa total del sistema.
Cuando realizamos nuestra experiencia de
Laboratorio, no tuvimos en consideración este hecho en razón de que la masa M
es mucho mayor que m.
6 Tercera Ley de Newton:
Hay varias situaciones de la vida cotidiana
donde se puede verificar el cumplimiento de la Tercera Ley de Newton. Veamos
algunos ejemplos:
a) cuando un arma de fuego es disparada se produce lo que llamamos
culetazo o retroceso.
b) si nos encontramos en un bote junto al muelle, para alejarnos
empujamos con el remo el muelle y el bote en consecuencia se aleja en sentido
opuesto al de la fuerza aplicada.
c) si nos encontramos en un bote junto a otro bote y empujamos a este
con el remo, veremos que ambos botes se mueven separándose.
d) cuando golpeamos con el puño, por ejemplo, una pared sentimos
dolor por el golpe simultáneo que recibimos de la pared.
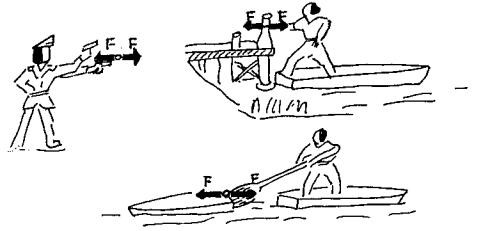
Con los ejemplos podemos concluir que un objeto
no puede ejercer una fuerza sobre otro sin que éste ejerza una fuerza sobre el
primero.
Estos ejemplos son verificaciones de lo que se
conoce como el Principio de Acción y Reacción o Tercera Ley de Newton.
“Siempre
que un cuerpo ejerce una fuerza sobre otro, este reacciona con una fuerza igual
y opuesta, aplicada sobre el primero”.
Denominamos acción
a la fuerza que un cuerpo ejerce sobre otro y reacción a la que éste ejerce sobre el primero. Es indistinto cuál
es reacción y cuál es acción. Debido a que toda acción va acompañada de su
reacción, lo correcto es decir que los cuerpos interaccionan, queriendo
significar esto, que existe una acción mutua de uno sobre el otro.
Debe quedar bien claro que la acción actúa
sobre un cuerpo y la reacción sobre el otro, de que son de igual intensidad y
de sentidos opuestos.
En el ejemplo del arma de fuego la acción actúa
sobre a bala y la reacción sobre el arma o inversamente.
En el ejemplo del muelle, la acción actúa sobre
el muelle y la reacción sobre el remo y el bote: podríamos preguntarnos:
¿porqué no se mueve el muelle como lo hace el bote?.
En el ejemplo de los patines la acción actúa
sobre la pared y la reacción sobre el patinador. Ocurre en este caso lo mismo
que con el muelle, la pared por acción de esta fuerza no se mueve.
Volveremos sobre éste principio más adelante y
allí lo analizaremos con más detalle, por ahora solo lo mencionamos a los
efectos de tener en cuenta las reacciones a las fuerzas aplicadas en nuestro
estudio introductorio de la dinámica.
7 Unidades de Masa y Fuerza:
Antes de aplicar las leyes de Newton a
situaciones reales tendremos que resolver el problema de las unidades en que se
miden la masa y la fuerza.
Las unidades en que se miden ciertas magnitudes
físicas, tales como longitud, tiempo, masa, fuerza, etc. se hacen mediante
definiciones y convenios, de carácter generalmente universal. Por ejemplo,
originariamente se definió metro como la diezmillonésima parte de la distancia
entre el Ecuador y el Polo Norte, tomada a lo largo del meridiano de Paris.
Luego por razones de practicidad se redefinió tomando al metro como la
distancia entre dos marcas practicadas sobre una barra de platino-iridio,
construida para tal fin (Metro Patrón). Actualmente existe otra definición con
mayores posibilidades de reproducirse en los laboratorios encargados de la
elaboración de patrones en cada uno de los países.
Para el caso de la masa, se eligió un cierto
objeto de material y dimensiones bien especificadas, asignándole
arbitrariamente el valor de una unidad de masa. Inicialmente se eligió la masa
de 1000 cm3 de agua a 4º C, pero esa elección no fue afortunada por
inconvenientes de carácter experimental. Para superar dichos inconvenientes, se
construyó un cilindro sólido, de una aleación altamente resistente (platino-iridio)
guardado actualmente en la oficina de Pesos y Medidas en Sévres (Francia). A la
masa de dicho cilindro se le asignó arbitrariamente el valor de un kilogramo.
La milésima parte de un kilogramo es lo que se denomina gramo. Casi todos los
países han adoptado como medida oficial el kilogramo. La excepción la
constituyen los países de habla inglesa (Inglaterra, EE. UU, Australia, etc)
que mantienen como unidad de masa a la libra, pero actualmente se define como
una fracción del kilogramo.
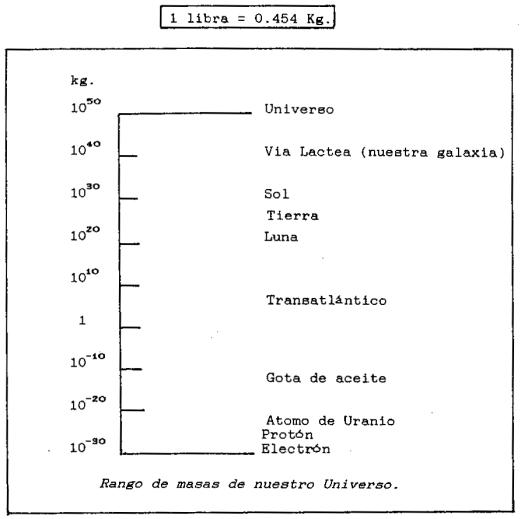
En la tabla anterior se muestra el rango de
masas de nuestro Universo, listando las masas de algunos objetos
característicos en correspondencia con la tabla de la izquierda donde figura la
masa de los objetos en kg. dada en notación científica (10n es diez
seguido de n ceros, 10-n es uno sobre 10 seguido de n ceros).
Hay unidades que se obtienen a partir de otras,
por ejemplo: la de superficie m2, que resulta de multiplicar metros
por metros. De igual manera resultan la de volumen: m3 También
entran en esta categoría las unidades de velocidad:
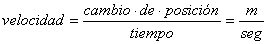
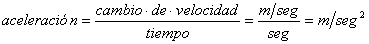
Estas unidades, generalmente se conocen como
unidades derivadas.
Dado que ya sabemos con que unidades se mide la
masa y la aceleración, utilizando la Segunda Ley de Newton podemos obtener la
unidad de fuerza.
Definimos como unidad de fuerza, aquella que a
la unidad de masa (1 kg.) le proporciona una aceleración unidad (1 m/s2
), o sea:
1 (unidad de
fuerza) = 1 Kg . 1m/s2
Esta unidad, por definición, se denomina NEWTON:
8 Sistemas de Unidades:
Un rápido repaso a la sección anterior, muestra
una diferencia en el modo de definir las unidades. Un grupo en el cual se
encuentran aquellas que se definen tomando un patrón, ya sea natural o
artificial, y conviniendo que será aceptado como referencia para las medidas.
Un segundo grupo en el cual las unidades se obtienen como combinación de otras
unidades.
Al primer grupo pertenecen el metro, el segundo
y el kilogramo. Estas unidades se denominan fundamentales. Al segundo grupo
pertenecen, por ejemplo, el m2, el m3, m/s, m/s2,
etc. Cuando agrupamos las unidades fundamentales y las unidades derivadas se
tienen lo que se denomina un Sistema de Unidades. Hemos venido usando algunas
unidades del Sistema M. K. S. . Decimos algunas porque hay muchas otras
magnitudes físicas cuyas unidades se incluyen en este Sistema, magnitudes
físicas que veremos en temas futuros.
El Sistema M. K. S es el más utilizado en
ciencia pero no es el único. Hay muchos, puesto que la selección de cuales son
las unidades fundamentales es hasta cierto punto arbitraria.
Por ejemplo: en el sistema c. g. s. la unidad de
longitud es el centímetro; la de masa, el gramo y la de tiempo el segundo (con
las iniciales de éstas cantidades se obtiene cgs); todas son unidades
fundamentales. En este sistema la unidad de fuerza es una unidad derivada y
puede obtenerse (F = m . a) como el producto de la unidad de masa (1 gr) por la
unidad de aceleración (1 cm/s2). Su nombre es dina:
Veremos más adelante otro sistema, en el que la
unidad de fuerza es fundamental y no lo es, en cambio, la unidad de masa.
|
Fundamentales
|
MKS
|
CGS
|
|
longitud
|
m.
|
cm.
|
|
tiempo
|
s.
|
s.
|
|
masa
|
Kg.
|
g.
|
|
Derivadas
|
|
superficie
|
m2
|
cm2
|
|
volumen
|
m3
|
cm3
|
|
velocidad
|
m/s
|
cm/s
|
|
aceleración
|
m/s2
|
cm/s2
|
|
fuerza
|
Newton
|
Dina
|
9 Peso de los cuerpos Masa y Peso
Al final de la unidad de cinemática, analizamos
experimentalmente cómo caen los cuerpos. Allí descubrimos que lo hacen con
movimiento uniformemente acelerado, es decir con aceleración constante.
¿Por qué caen los cuerpos?. Esta pregunta es
importante pues la caída de los cuerpos es un fenómeno muy frecuente, mejor
dicho, permanente en nuestra vida diaria. Hay varias respuestas para esta
pregunta, algunos dirán: "porque pesan", otros con más precisión
dirán "porque la Tierra atrae los cuerpos". En efecto, la Tierra
atrae los cuerpos, pero esta no es una propiedad exclusiva de ella, sino que
todos los cuerpos atraen a los otros cuerpos. Cualquier cuerpo o conjunto de
cuerpos, tan pequeños o grandes como queramos, cercanos o lejanos, se atraen
mutuamente, con una fuerza llamada fuerza gravitatoria.
El fenómeno de la acción gravitatoria es un
fenómeno universal, es decir válido para todo el Universo. Existen numerosos
fenómenos que tienen su origen o son determinados por la fuerza de atracción
gravitatoria: la caída de los cuerpos, el movimiento de la Luna alrededor de la
Tierra, y de ésta alrededor del Sol, y del Sol alrededor del centro de nuestra
galaxia, etc. Más adelante veremos en detalle esta Ley de Gravitación. Por
ahora continuamos con su manifestación más evidente a nuestros sentidos: la
caída de los cuerpos.
El valor de la aceleración con que caen los
cuerpos en el vacío no depende de la masa del cuerpo, depende de la masa de la
Tierra y de la distancia entre el cuerpo y el centro de la Tierra. Para un
cuerpo que se encuentra próximo a la superficie terrestre, a 45º de
latitud y a nivel del mar, el valor de la aceleración gravitatoria es g = 9,8
m/s2.
Debido a que la Tierra no es esférica hay
variaciones de g por la latitud, aumenta en los polos (g = 9,83 m/s2)
y disminuye en el Ecuador (g = 9,78 m/s2). Para un mismo lugar en la
superficie terrestre, disminuye a medida que aumenta la distancia al centro de
la Tierra.
Resulta difícil aceptar, que en un mismo lugar,
todos los cuerpos caen con la misma aceleración en el vacío, independientemente
de sus pesos (o masas); esto es así porque generalmente no se repara en la
condición de que la afirmación es válida solo para el vacío. La razón de la
dificultad está en que las diferencias que observamos en la vida diaria se
deben a que el cuerpo que cae lo hace a través del aire, lo cual implica
rozamiento y por tanto resistencia a que el cuerpo caiga. Ejemplo: una hoja de
papel tardará tiempos distintos en caer la misma altura según que caiga
extendida o arrugada hecha una pelotita. Verifíquelo. En cambio si lo hace en
el vacío en ambos casos tardará el mismo tiempo.
Resuelta la pregunta de porqué caen los cuerpos
corresponde ahora determinar cuál es el valor de la fuerza con que la Tierra
los atrae. Para ello apliquemos la Segunda Ley de Newton (F = m . a), a este
caso. La aceleración a debe remplazarse por la aceleración de la gravedad g, y
la fuerza con que el cuerpo es atraído por la Tierra es lo que denominamos peso
del cuerpo e indicaremos con P. Por lo tanto, la ecuación anterior toma la
forma:
Ejemplo: ¿Cuánto pesa un cuerpo de masa 10 kg.
en un lugar de aceleración gravitatoria normal?
m = 10 kg. g = 9,8 m/s2
P = 10 kg . 9,8
m/s2 = 98 Newtons.
Aquí se hace evidente la diferencia entre peso y
masa de un cuerpo. Generalmente se confunden, pero son fundamentalmente
magnitudes físicas distintas, pues la masa es una propiedad intrínseca del
cuerpo y no depende del lugar en que se encuentre, ni de las condiciones
externas al cuerpo; mientras que el peso depende de la posición que tiene,
respecto del centro de la Tierra.
Antes de finalizar es necesario hacer una
aclaración respecto a las unidades de peso, para evitar futuras confusiones. En
el ejemplo anterior se calculó el peso de una masa de 10 kg y se obtuvo un
resultado en Newton. Sin embargo en la vida diaria cuando hablamos del peso de
las cosas no hablamos de Newtons, sino de Kilogramos. ¿Acaso Kilogramos no es
una unidad de masa?. ¿A qué se debe la confusión?. Se debe a que se usa la
misma palabra para nombrar dos cosas diferentes. Existen el Kilogramo-fuerza
(Kgr. ) y el Kilogramo-masa (Kg). Este último ya lo vimos al introducir las
unidades de masa.
Se define como Kilogramo-fuerza al peso de 1
kg-masa cuando se lo mide a nivel del mar y a 45º de latitud, o
sea en un lugar donde g = 9,8 m/s2.
Tomando, la longitud, el tiempo y la fuerza como
medidas fundamentales se obtiene un nuevo Sistema de Unidades: el Sistema
Técnico. En este sistema la unidad de masa es una unidad derivada y se denomina
Unidad Técnica de Masa, y se indica UT(m).
La masa de un cuerpo, en el Sistema Técnico, se
obtiene de dividir su peso en Kg-fuerza por la aceleración de la gravedad.
Ejemplo 1: ¿Cuál es la masa, en el Sistema Técnico, de un cuerpo que pesa 1
Kgr?. (NOTA: indicaremos con Kgr. el Kilogramo-fuerza y con Kg. el
kilogramo-masa)
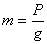
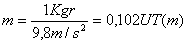
Ejemplo 2: ¿Cuál es la masa de un hombre que pesa 70 Kgr. ?
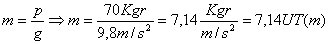
Ejemplo 3: ¿Cuánto pesa 1 UT(m)?
P = m. g à P = 1 UT(m) . 9,8 m/s2
P = 9,8 UT(m) .
m/s2 à P = 9,8 kgr
P = 9, 8 UT(m).
m/s ~ P = 9, 8 kgr.
Ejemplo 4: ¿Cuánto pesa en la Luna un hombre que pesa 70 kgr en la Tierra?.
La gravedad en la Luna vale 1,67 m/s2.
P = m . 1,67 m/s2
Por el ejemplo 2, si pesa en la Tierra 70 Kgr.,
su masa en UT(m) es 7, 14 UT(m), por lo tanto:
P = 7,14 UT(m) .
1,67 m/s2
P = 11,92 Kgr.
En sección Problemas calcularemos las
equivalencias entre unidades de fuerza y masa en los distintos sistemas.
Ejemplo "peligroso": Calcular la masa
en Kg. (Sistema MKS) de un hombre que pesa 70 Kgr (Sistema Técnico).
Dado que por definición el Kilogramo patrón que
pesa 1 kgr. tiene una masa de 1 Kg. resulta:
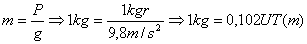
y recíprocamente:
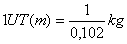 o
sea
o
sea
1 UT(m) =
9,8 Kg
Por el ejemplo 2 la masa de un hombre que pesa
70 Kgr es 7,14 UT(m), y teniendo en cuenta la equivalencia última:
7,14 UT(m) = 7,14 . 9,8 kg = 70 kg
¡CUIDADO!, son 70 Kg de masa
Es decir, un hombre que pesa 70 Kgr. (Sistema
Técnico) tiene una masa de 70 kg. (en el Sistema MKS).
Pero eso NO significa que peso y masa sean lo
mismo. La igualdad numérica entre lo que indica el peso, en un sistema, y lo
que indica la masa, en el otro, más la desafortunada circunstancia de que se
usa la misma palabra, Kilogramo, para nombrar dos magnitudes distintas, peso y
masa; ha generado la incorrecta costumbre de usar la unidad de peso para
indicar masa.
Por ejemplo: cuando colocamos una pesa de masa 1
kg. en un platillo y una masa de 1 Kg. de azúcar en el otro platillo de la
balanza, ésta queda en equilibrio. Si la gravedad en ese lugar tiene el valor
normal g = 9,80 m/s , el peso de ambas cosas es de 1 kgr. Si cambiamos de lugar
la balanza, a otro lugar de g distinto, la masa de la pesa y del azúcar no
cambian, en cambio su peso si.
Esto se podría verificar con un dinamómetro,
aparato constituido por un resorte y una escala. Este aparato mide fuerzas en
unidades técnicas: Kgr. Si cuelgo en un lugar de g = 9,8 m/s2 una
masa de 1 kg., el dinamómetro indicará una fuerza de 1 kgr. Si luego me
traslado con el dinamómetro y la masa colgando, a un lugar de g distinta,
VARIARA la indicación en la escala; pues el peso del cuerpo ha variado al cambiar
g.
Las variaciones de g, a lo largo y a lo ancho de
la superficie terrestre no son tan grandes como para hacer muy evidentes estas
variaciones de peso, pero ellas existen. Por lo tanto convengamos en que:
cuando decimos que un cuerpo pesa x Kilogramos, nos estamos refiriendo al peso
que tiene en ese lugar
dicho cuerpo. Si allí g = 9,80 m/s el peso será numéricamente
igual a la masa. En caso contrario será levemente distinto.
NOTICIA
Se informa a
los lectores e interesados que el presente número de esta Revista y algunos
anteriores están a su disposición en la página web de la Universidad Nacional
de San Luis, en la sección Bibliotecas, publicaciones en
linea:
http://bib0.unsl.edu.ar/bibls/publ-online.html
Para consultas,
sugerencias, etc., puede hacerlo por correo electrónico:
Email: cmaga@unsl.edu.ar



































