
EL PROFESOR
DE CIENCIAS

EL PROFESOR
DE CIENCIAS
Número 12 JULIO/2000
Facultad de Ciencias Físico Matemáticas y Naturales
Universidad Nacional de San Luis
OBJETIVOS
Esta publicación está destinada a Profesores de Nivel Medio en Matemáticas y Física.
El objetivo fundamental es establecer una comunicación directa de la Facultad de Ciencias Físico Matemáticas y Naturales (UNSL) con dichos Profesores, a efectos de desarrollar actividades que permitan mejorar la calidad de su enseñanza en estas ciencias y, por lo tanto, mejorar la calidad de sus egresados.
El contenido de esta publicación estará constituido por artículos metodológicos e instrumentales para la enseñanza teórica y práctica de temas del currículum de nivel medio, problemas y su metodología de resolución, desarrollo de temas de actualidad en relación a su aplicación al currículum, prácticos de laboratorio, preguntas y respuestas para transferencia de conocimientos, noticias de carácter educativo en el área, evaluación, cartas, comentarios y artículos enviados por los docentes-lectores, donde puedan aportar, solicitar o compartir sus logros, necesidades, dudas y, finalmente todo artículo cuyo contenido los profesores soliciten, sugieran o sea oportuno incluir.
Señor Profesor:
Para lograr el propósito de mantener la edición de esta publicación, se necesita de la respuesta y colaboración de los destinatarios. Esto significa que es muy necesario, y se lo agradecemos desde ya, nos haga llegar sus opiniones, solicite y aplique el material que le ofrecemos, envíe artículos para publicar y difunda esta pequeña revista.
Muchas Gracias
INDICE
Publicación subsidiada por la Facultad de Ciencias Físico Matemáticas y Naturales de la Universidad Nacional de San Luis
IDEA Y REALIZACION: Lic. Carlos Magallanes
PUBLICACION EN Web: Prof. Germán Roque Arias
Sabía Ud. que ...
A principios del Siglo 17, J. Kepler desarrolló la teoría de la marcha de rayos para la construcción de imágenes formadas por lentes delgadas.
Entonces se introdujo el concepto de eje óptico, foco y distancia focal de una lente.
DE LA FÍSICA
Desde el punto de vista de los alumnos (nivel medio) el estudio de la Física es una tarea difícil y sin sentido. Esta ultima objeción puede explicarse cuando se observan las clases de los Profesores y se leen la mayoría de los textos que se aplican.
Se ha extraído a la Física del mundo real, se la ha transformado en ecuaciones y números que se despliegan en el pizarrón. Esto explica la mala fama ganada injustamente por la Física en el conjunto de los alumnos.
La descontextualización de la Física ha transformado su rico contenido en una serie de conceptos, ecuaciones y leyes que exigen de los alumnos un proceso de abstracción e imaginación que no logran alcanzar. Esto conduce a su fracaso en su aprendizaje , su desmotivación y desaliento.
El intento del Profesor de darle sentido concreto a lo enseñado, cuando da problemas de aplicación, no remedia el fracaso anterior cuando pretendió que sus alumnos “ vean y lean” en una ecuación todo un proceso físico con sus parámetros y variables en acción.
La incorporación de un contexto donde introducir los conceptos y contenidos de una unidad temática muestra al alumno que es posible y necesario definir magnitudes físicas para denominar o describir una parte o todo un fenómeno físico.
La incorporación de estas magnitudes y la evolución del fenómeno en el contexto elegido permitirá establecer relaciones entre ellas y de allí obtener una descripción completa de los contenidos de la unidad temática elegida.
En una segunda etapa , se sale del contexto para pasar a otro, allí aplicar los conceptos aprendidos en la etapa anterior y luego generalizar para cualquiera.
Este proceso implica, cuando es posible, introducir al alumno en el contexto mismo hacerlo sentir o percibir de algún modo la física que las magnitudes introducidas describen.
Esta condición hace que la elección del contexto sea algo delicado. Tiene que ser accesible a los alumnos y estar vinculado a sus actividades e intereses. No debe ser complicado ni difícil de describir en pocas palabras.
A continuación se ejemplifica lo anterior mediante una planificación para la unidad temática: cinemática. En ella se describe el contenido de la unidad, su esquema conceptual, los objetivos , una planificación con detalle de las actividades y una guía para el Profesor con explicaciones aclaratorias.
Respecto de los objetivos, se los se han determinado dentro del esquema de los Objetivos Delphi.
Estos tienen en cuenta un aspecto generalmente ignorado por la enseñanza actual de las ciencias naturales y la matemáticas. El análisis de este aspecto seria largo de analizar, pero, en pocas palabras , se quiere significar que la función del profesor no es solo enseñar Física. Su función es, por encima de todo, la formación de un individuo incorporado a una sociedad que necesita un producto capacitado y concientizado de su importancia dentro de ella. Este individuo debe tener capacidad , ser responsable y solidario en la utilización de sus conocimientos y aplicación del saber científico y tecnológico.
La cinemática es un tema que debe ocupar uno de los primeros lugares en un currículum de Física por la necesidad de introducir conceptos básicos en el estudio de otros temas de igual importancia , tales como dinámica, trabajo, energía, impulso, etc.
Su relación con magnitudes fácilmente medibles permite una aplicación inmediata de las matemáticas y la deducción de ecuaciones. Esta condición hace que: a) se exagere el tiempo dedicado a hacer ejercicios con estas ecuaciones y b) para poder hacer esto se saca a la cinemática del mundo real y se lleva todo al pizarrón, lugar en que la física, para el alumno, desaparece. Esto genera poca eficiencia en la comprensión de los conceptos y conduce a la desmotivación.
La incorporación de un contexto perteneciente al mundo real e inmediato al alumno y que le genere interés es una vía más que conveniente para lograr motivación y aprendizaje. Un contexto apropiadamente elegido para un conjunto de temas puede despertar la curiosidad en el alumno y esto conducirlo a indagar por si mismo y , además, encontrarle sentido a lo que está estudiando.
Debe recalcarse que cualquier contexto no siempre será apropiado para todo grupo de alumnos.
En esta propuesta se elige el campo de fútbol como contexto de fondo para el estudio de los movimientos más frecuentes en nuestra vida diaria. Si se hubiese elegido un campo de baseball, salvo a una minoría, esta elección no poseería la cuota de motivación necesaria para el objetivo de la unidad. En caso de un subgrupo que no se interese por el fútbol, es conveniente elegirle otro contexto.
Es importante aclarar que el usar un contexto como apoyo para el desarrollo de una unidad temática no implica que todo el contenido se relacionará al mismo. El contexto sirve como punto de partida, fuente de motivación permanente y referencia.
Se inicia el estudio de un conjunto de conceptos dentro del contexto, luego se aplica lo aprendido a otras situaciones extra- contexto y finalmente se generaliza.
De acuerdo a las exigencias metodológicas se debe utilizar el contexto en forma alternativa. El criterio del Profesor determinará la profundidad, contenido y oportunidad de estas interacciones.
Movimientos rectilíneos. Posición, velocidad y aceleración media e instantánea. Movimiento rectilíneo con velocidad constante. Ídem con aceleración constante.
Cinemática en dos dimensiones: Posición, Desplazamiento, Velocidad y Aceleración. Carácter vectorial de estas magnitudes. Tiro vertical, oblicuo y horizontal de un proyectil en un campo gravitatorio. Construcción e interpretación de gráficas de las magnitudes cinemáticas en función del tiempo. Movimiento Circular: velocidad lineal y aceleración centrípeta y tangencial.
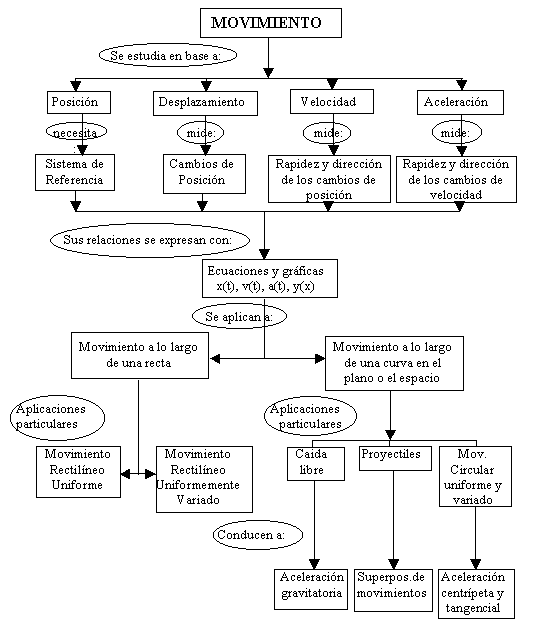
1- Observar, caracterizar y establecer diferencias de los movimientos posibles de los jugadores, los árbitros y la pelota en un partido de fútbol
2- Comprender como la acción coordinada y un objetivo común permite la obtención de un logro.
3- Comprender que en la acción conjunta, a favor o en contra, de un grupo de personas hay normas que respetar para poder convivir.
4- Analizar y entender las definiciones de las distintas magnitudes físicas que intervienen en la descripción de los movimientos.
5- Adquirir habilidad para determinar velocidades, desplazamientos y aceleraciones en los movimientos en una y dos dimensiones.
6- Ser capaz de construir e interpretar gráficas x(t), v(t), a(t) a partir de tablas y gráficos.
7- Comprender la importancia del carácter vectorial de las magnitudes cinemáticas.
8- Ser capaz de obtener gráfica y analíticamente las componentes de magnitudes vectoriales en dos direcciones prefijadas.
9- Comprender como se puede regular la dirección y alcance de un tiro oblicuo mediante el ángulo y la velocidad inicial.-
10- Observar la acción retardadora de las fuerzas de rozamiento tanto en la rodadura de una esfera sobre una superficie como en el caso del movimiento a través del aire.
11- Adquirir habilidad en el manejo de las ecuaciones que relacionan las magnitudes cinemáticas en los distintos movimientos estudiados.
12- Observar y comprender como el estudio previo y planificación puede llevar a resultados positivos o negativos por la acción de factores ajenos y el comportamiento propio.
13- Observar y apreciar en su medida como la incorporación de tecnología al deporte ha permitido el logro de mas eficiencia en su práctica. Por otra parte también la tecnología ha permitido que mayor cantidad de gente pueda compartir un evento deportivo en cualquier lugar del mundo, y, a veces, en el mismo momento del suceso.
14- Adquirir el hábito de ser equilibrado y justo en las disputas deportivas y aceptar los errores y virtudes propias y del adversario.
15- Reconocer el daño físico y social que provocan algunos hinchas descontrolados con desmanes y provocaciones y que ningún mal arbitraje o resultado adverso de un partido justifica cualquier violación a las normas de convivencia y derechos de nuestros semejantes.
16- Reconocer el papel fundamental de la aceleración gravitatoria en el movimiento de los cuerpos próximos a la superficie terrestre.
17- Comprender el principio de superposición de movimientos a través del tiro oblicuo.
18- Comprender el papel de la aceleración centrípeta en cualquier movimiento no rectilíneo.
19- Comprender la razón Física de la posición y dirección del vector velocidad instantánea en cualquier movimiento.
20- Comprender la función de las componentes tangencial y centrípeta de la aceleración en cualquier movimiento donde no sean nulas.
21- Adquirir normas de comportamiento social.
22- Comprender como el entrenamiento específico en ciertas disciplinas permite un rendimiento físico sobresaliente.
23- Comprender la importancia del “efecto” (spin) tanto en el fútbol como en otros deportes.
|
Video de presentación del contexto; Movimientos en una cancha de fútbol. Práctico de Aula Nº 1: Identificación, caracterización e inventario de todos los movimientos posibles de los distintos participantes durante el desarrollo de un partido de fútbol. Práctico de Aula Nº 2 : Movimiento del Juez de línea Gráfica x(t). Definición de velocidad media Gráficas v(t) Trabajo de Campo Nº 1: registro x(t) del movimiento del Juez de línea en un partido el domingo siguiente ( o de un video seleccionado). Trabajo de Campo Nº 2: registro x(t) de un desplazamiento en moto o en auto a lo largo de una calle con semáforos. Trabajo de Campo Nº 3 : registro x(t) de una caminata a lo largo de una galería, con trayectos recorridos con distinta rapidez y con paradas de distintas duraciones. |
1º Módulo Presentación Contextualizada |
|
Práctico de Aula Nº 3 : movimiento de un móvil a lo largo de una línea recta. Análisis de los resultados de los trabajos de campo Gráficas x(t) , calculo y gráfica de v(t) Tratamiento general del tema Mov. Rect. con Velocidad constante. (MRU) .Problemas de aplicación. |
2º Módulo Presentación generalizada |
|
Práctico de Aula Nº4 : Sesión de video, registro (x,y) de las posiciones de un jugador que parte del centro del campo, elude jugadores llega al arco y convierte gol. Práctico de Aula Nº 5: En un sistema de referencia definido en la cancha, dibujar vectores posición, desplazamientos parciales y total. Definición de posición, desplazamiento, velocidad media e instantánea. Carácter vectorial de estas magnitudes. Práctico de Aula Nº 6: Repetir proceso anterior pero registrando las posiciones de la pelota solamente, a partir de un trozo de video seleccionado.(Todos los pases son cortos, horizontales a nivel del suelo) Trabajo de Campo Nº 4: En un partido entre los alumnos ( o de un video seleccionado) efectuar el registro de las distintas posiciones de la pelota en un intervalo de tiempo y construir su trayectoria (gráfica y(x)) |
3º Módulo Presentación contextualizada |
|
Clase del Profesor para resumir, sistematizar y generalizar la información acumulada en los prácticos de aula y de campo respecto a: sistema de referencia, posición, desplazamiento, velocidad ( media e instantánea). Carácter vectorial. Gráficas x(t), v(t) e y(x). Problemas de aplicación. Debate:violencia y mala intención en el campo de juego.Respeto al árbitro. Autocontrol de los deportistas. |
4º Módulo Presentación Generalizada |
|
Trabajo de Campo Nº 5 : lanzamiento vertical de una pelota con un puntapié y/o con la mano. Observación del comportamiento de las magnitudes ya definidas Práctico de Aula Nº 7 : Lanzamiento vertical de un proyectil con una cerbatana.Observación de la velocidad (especialmente cuando alcanza la altura máxima ( v = 0) Práctico de Aula Nº 8: caída libre de objetos. Registro del comportamiento de las magnitudes estudiadas Tiro vertical .Comparación de observaciones y conclusiones. |
5º Módulo Presentación Contextualizada |
|
Resumen de las experiencias anteriores. Definición de aceleración ( media e instantánea). Aceleración en el campo de fútbol. Caso particular: aceleración gravitatoria. Mov. Rect. con aceleración constante(MRUV). Gráficas y ecuaciones. Problemas de aplicación a aceleración de un futbolista, tiro penal, de un automóvil, de un ciclista, etc. |
6º Módulo Presentación Generalizada |
|
Pase de la pelota por elevación. Regulación de la Velocidad inicial, dirección, altura y alcance del pase. Tiro libre por elevación con y sin efecto. Lanzamiento del arquero. Observación de videos. Dibujo de trayectorias. Práctico de Aula Nº 9: Análisis del comportamiento de las magnitudes cinemáticas durante el vuelo de la pelota. Trabajo de Campo Nº 6: lanzamiento de pelotas (con el pié y con la mano) con distintos ángulos y/o velocidades para lograr distintas alturas y/o alcances. Problemas de aplicación dentro y fuera del contexto. Debate: violencia fuera del campo de juego. Autocontrol del hincha. Derechos Humanos y Privados. |
7º Módulo Presentación Contextualizada |
|
Práctico de Aula Nº 10 : Observación de un tiro oblicuo en el aire (cerbatana). Medición de alturas máximas y alcances. Análisis de los movimientos horizontal y vertical Superposición de movimientos. Velocidades y aceleraciones en el tiro oblicuo y horizontal. Ecuaciones de x(t), v(t) y de la trayectoria. Problemas de aplicación. |
8º Módulo Presentación Generalizada |
|
Rotación y rodadura. Semejanzas y diferencias. Trayectoria de un cuerpo girando y otro rodando. Práctico de Aula Nº 11: Rotación de una pelota. Comportamiento del desplazamiento, velocidad y aceleración en este movimiento. |
9º Módulo Presentación Contextualizada |
|
Movimiento Circular uniforme. Movimiento de un punto de un cuerpo en rotación. Aceleración centrípeta. Velocidad tangencial. Movimiento Circular variado. Aceleración tangencial. Movimiento curvilíneo general. Función de las componentes centrípeta y tangencial en este movimiento. |
10º Módulo Presentación Generalizada |
Esta guía tiene por objetivo describir ideas y sugerencias para las actividades detalladas en el desarrollo sugerido en paginas anteriores.
Por Práctico de Aula (PA) se quiere significar actividades a desarrollar en el Aula o Laboratorio. Aquí se resuelven cuestiones , problemas o se efectúan experimentos.
Por Trabajo de Campo (TC) se significa actividades a desarrollar por los alumnos en forma independiente o con la guía del Profesor cuando este lo considere necesario. Estas actividades se desarrollan fuera del aula y dentro o fuera del contexto elegido.
El objetivo es indagar en base a conocimientos ya adquiridos o en la búsqueda de información previa para la obtención de otros.
Esta guía de ningún modo pretende que el profesor se ajuste estrictamente a ella. Solo son sugerencias para generar nuevas ideas de acuerdo a la creatividad y posibilidades del docente.
La presentación de la Unidad se puede hacer en base a un video seleccionado de tal modo que los alumnos puedan identificar todos los tipos de movimiento que se producen en un partido de fútbol.
En el PA Nº 1 se deben observar los movimientos del juez de línea, de un jugador en particular, del arbitro y de la pelota. Procure que el inventario se haga en términos de traslación y rotación.
Los alumnos tienen ya una idea de velocidad y aceleración, en especial de la primera. Tome nota de la interpretación que ellos tienen pero no la discuta ni rechace aun.
Para el PA Nº 2 procure conseguir un video que muestre el desplazamiento del juez de línea en un intervalo de tiempo suficiente para observar desplazamientos en ambos sentidos u momentos de reposo. Haga redactar un texto donde se describa el movimiento del juez. Represéntelos en un esquema de la cancha y a escala procurando estimar las distancias y tiempos en que cambia el movimiento. En caso de no conseguir el video deberá hacer este registro previamente y presentárselo a los alumnos. El objetivo de este PA es que los alumnos vean que este movimiento se puede realizar en una sola dirección y en dos sentidos y en algunos momentos permanecer en reposo. Aquí puede introducir la idea de velocidad media.
Para el TC Nº 2 se recomienda organizar el curso en grupos y dar consignas de movimiento rectilíneo en la galería del colegio por escrito a cada grupo. En cada grupo habrá alumnos que efectúan los desplazamientos , otros que dictan las consignas y que toman los tiempos. Luego cada grupo redactará un texto con los movimientos efectuados y construirán las graficas x(t). Uniendo ambos resultados explicarán la grafica a sus compañeros.
Debe cuidar el Profesor que los alumnos comprendan que lo que han obtenido es un gráfico y que su forma NO representa la trayectoria. Esta advertencia debe ser tomada seriamente en cuenta. También es el momento oportuno para que en los gráficos x(t) los alumnos asocien pendiente con velocidad . Ellos han percibido en forma personal que el caminar mas rápido implica mayor velocidad y que en la grafica la parte de x(t) correspondiente tiene mas pendiente.
El TC Nº 3 puede asignarse como trabajo para la casa y luego ser discutido en la clase siguiente. Es importante rescatar aquí el relato con que el alumno describe el movimiento y su lectura en la grafica x(t).
En el segundo módulo se sale del contexto inicial para desarrollar en forma mas rigurosa las ideas y conceptos tratados en la etapa anterior y en un contexto mas general. Se recomienda para esta parte el capitulo de cinemática en una dimensión del texto PSSC (Reverté).
Para el PA Nº 4 se recomienda que la clase tenga conocimiento o una base de datos de las dimensiones y distancias importantes de una cancha de fútbol: largo, ancho, distancia área chica y grande, etc. Esto es necesario para aprovechar el práctico para que los alumnos aprendan a estimar distancias, en base a una referencia, y tiempos. En Física muchas veces es suficiente una estimación de las magnitudes para estudiar un hecho físico.
En el PA Nº 5 si no tiene acceso a una cancha , si la tendrá al patio de la escuela o a un terreno vacío. Con marcas de tiza, pintura ,etc, señale el sistema de referencia. En ultimo caso con piolines y clavos como hacen los albañiles. Lo importante es que no lo haga dentro del aula y mucho menos en el pizarrón. Al menos en esta etapa introductoria.
El TC Nº 5 tiene como objetivo introducir dentro del contexto elegido el movimiento con aceleración. La observación directa y los conocimientos sobre posición y velocidad, permiten deducir que hay una variación en la velocidad de la pelota, punto de partida para el concepto de aceleración. Lo que no es visible es que la aceleración es constante (conserva su dirección, magnitud y sentido).
En el movimiento vertical el error que suele persistir es la creencia de que la aceleración gravitatoria no está presente durante todo el movimiento. Todo lo contrario, el alumno debe quedar convencido de lo opuesto, incluso en el momento en que v = o, cosa que le cuesta aceptar.
Cuando se repite el práctico con la cerbatana se analiza el mismo experimento pero en otro contexto. Con el PA Nº 8 se completa el proceso de generalización y abstracción de los resultados.
Los debates propuestos en los módulos 4º y 7º son al efecto de cumplir con la parte formadora de la Escuela, en este caso, a través de la asignatura Física y de acuerdo a los objetivos mencionados en páginas anteriores. Se recomienda invitar al debate a personas que viven el problema: jugadores, árbitros, hinchas y dirigentes del fútbol.
Para quienes gustan de los parques de diversiones, he aquí el análisis físico de las sensaciones que percibe una persona (en adelante el pasajero) que participa en un viaje en la rueda gigante.
La rueda gigante tiene un radio del orden de los 10 metros. Consiste de dos grandes aros paralelos unidos por travesaños donde se cuelgan los asientos de los pasajeros y que gira en un plano vertical.
Indicaremos con m la masa de nuestros viajeros y con R el radio de la rueda.
Cuando la rueda está funcionando, el viajero efectúa un movimiento circular uniforme. Si indicamos con T el período del movimiento (tiempo con que la rueda da una vuelta completa), la frecuencia (cantidad de vueltas por unidad de tiempo) está vinculada con T de acuerdo a
![]()
Por ser un movimiento circular uniforme, actúa sobre el pasajero, además de su peso, una fuerza centrípeta. Las ecuaciones relacionadas a esta fuerza centrípeta son:
![]()
![]()
![]() (1)
(1)
En (1) para una rueda y un pasajero fijo, la única variable es f. Por eso escribimos
![]()
![]() (2)
(2)
La forma de la ecuación que da Fc en forma vectorial es
![]() (3)
(3)
Siendo ![]() un vector
unitario que apunta desde el centro de la rueda hacia la posición del pasajero.
un vector
unitario que apunta desde el centro de la rueda hacia la posición del pasajero.
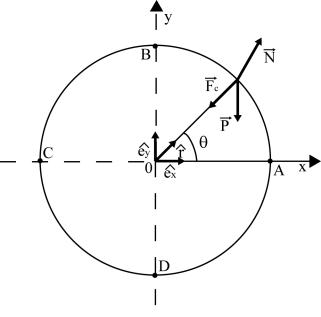
Fig. 1
En la expresión (3) se nota que Fc apunta siempre hacia
el centro 0. En Fig. 1 se indica el perfil de la rueda, la fuerza centrípeta
![]() , el peso
del pasajero
, el peso
del pasajero ![]() , el vector
unitario
, el vector
unitario ![]() y el ángulo
y el ángulo
![]() que este
forma con la horizontal.
que este
forma con la horizontal.
![]() se empieza
a medir desde el semieje positivo del eje horizontal x.
se empieza
a medir desde el semieje positivo del eje horizontal x.
También en Fig. 1 se indica el vector reacción
![]() . Este vector
representa la fuerza de reacción sobre el pasajero ejercida por el cinturón
de seguridad, el respaldo y el asiento sobre el que se encuentra sentado.
. Este vector
representa la fuerza de reacción sobre el pasajero ejercida por el cinturón
de seguridad, el respaldo y el asiento sobre el que se encuentra sentado.
Estas tres fuerzas tienen una resultante nula, pues el pasajero se encuentra en reposo respecto del asiento en el que viaja.
Entonces vale
![]()
Para describir las sensaciones que siente el viajero
durante una vuelta analizaremos la fuerza de reacción ![]() .
.
![]()
La descripción es mejor si descomponemos las fuerzas
en componentes rectangulares x, y. Definimos por eso dos vectores unitarios,
uno sobre el eje x: ![]() y otro sobre
el eje y:
y otro sobre
el eje y: ![]() (ver Figura
1).
(ver Figura
1).
De acuerdo a esto resulta:
![]()
![]()
![]() (4)
(4)
![]() (5)
(5)
La ecuación (5) da las componentes en dirección horizontal y vertical de la fuerza que percibe el pasajero.
Analicemos estas componentes cuando ya la rueda está girando en un régimen estacionario.
Para ![]() = 0 (Punto
A en Fig. 1) se ve que
= 0 (Punto
A en Fig. 1) se ve que ![]() y
y ![]() .
.
El pasajero siente su peso normal y que aumenta la presión del respaldo del asiento.
Para ![]() = 90º (Punto
B en Fig. 1)
= 90º (Punto
B en Fig. 1)
![]() ,
,
![]()
El pasajero siente pesar menos y no siente presión del cinturón ni del respaldo del asiento.
Para el valor de f que hace ![]() sentirá
la ingravidez o sea la sensación de no tener peso. Ese valor de f es:
sentirá
la ingravidez o sea la sensación de no tener peso. Ese valor de f es:
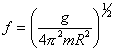
¡Cuidado!. Es una sensación del pasajero, él sigue pesando lo mismo que cuando está en reposo.
Cuando ![]() se repite
la situación de
se repite
la situación de ![]() pero ahora
pero ahora
![]() tiene sentido
opuesto. O sea el observador siente que aumenta la presión del cinturón.
tiene sentido
opuesto. O sea el observador siente que aumenta la presión del cinturón.
Para ![]() (punto
D en Fig. 1)
(punto
D en Fig. 1)
![]() ,
,
![]()
El pasajero siente que aumenta su peso. El cinturón y el respaldo no aumentan la presión que ejercen.
Resumiendo, en el primer y cuarto, cuarto de vuelta, la componente
![]() , el pasajero
siente que aumenta la presión del respaldo del asiento, mientras que en el segundo
y tercer cuarto, esta sensación la percibe originada en el cinturón de seguridad.
, el pasajero
siente que aumenta la presión del respaldo del asiento, mientras que en el segundo
y tercer cuarto, esta sensación la percibe originada en el cinturón de seguridad.
Por otra parte, en el primer y segundo cuarto de vuelta, el pasajero siente que disminuye la presión del asiento, en cambio en el tercer y cuarto cuarto de vuelta, esta presión aumenta, con un máximo en el punto mas bajo.
PREGUNTA
Ud. tiene que dar una clase de electrostática y debe preparar una demostración en poco tiempo.
Como no tiene los elementos apropiados recurre a dos latas de gaseosa vacías (masa de cada una m). Pega el extremo de un hilo delgado y liviano en el centro de la tapa de cada una y las cuelga desde un punto común. Los hilos tienen la misma longitud.
Con una máquina electrostática carga ambas latitas. A causa de la repulsión entre las cargas, éstas se separan hasta que los hilos forman un ángulo a = 10º.
En clase un alumno le pregunta como se hace para estimar la carga distribuida entra las latitas?, ¿Qué le contesta?.
Para hacer rodar un cilindro de radio R se suele aplicar una fuerza horizontal con punto de aplicación en un punto diametralmente opuesto al eje instantáneo de rotación.
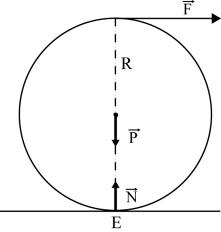
Fig. 1
En Fig. 1 se puede observar que aplicando ![]() en estas
condiciones se obtiene el máximo momento para generar la rotación respecto del
eje instantáneo indicado allí con E.
en estas
condiciones se obtiene el máximo momento para generar la rotación respecto del
eje instantáneo indicado allí con E.
¿Cambia (o nó) la afirmación anterior si el cilindro encuentra un escalón rectangular de altura h?
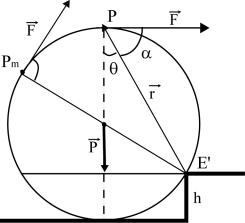
Fig. 2
En primer lugar debemos notar que cuando el cilindro
llega al escalón, para que continúe avanzando lo debe ascender. Cuando comienza
este ascenso la normal ![]() de Figura
1 se anula y ahora aparecerá en el nuevo eje instantáneo de rotación E’ (Fig.
2).
de Figura
1 se anula y ahora aparecerá en el nuevo eje instantáneo de rotación E’ (Fig.
2).
En Fig. 2 se indica el nuevo eje de rotación E’, la fuerza ![]() aplicada
en el punto P (genérico), el vector posición
aplicada
en el punto P (genérico), el vector posición ![]() de P respecto
al eje E’ y a el ángulo
que forman
de P respecto
al eje E’ y a el ángulo
que forman ![]() y
y ![]() .
.
El momento de rotación que nos interesa es el de
la fuerza ![]() , por su
definición:
, por su
definición: ![]() .
.
A simple vista se ve que cuando ![]() ,
, ![]() será máximo
y que esto se logra en la posición
será máximo
y que esto se logra en la posición ![]() de la fuerza
de la fuerza![]() .
.
Observe que Pm está diametralmente opuesto al eje de rotación E’. O sea la misma conclusión obtenida para el caso de rodadura en un plano horizontal.
Esta afirmación se puede verificar matemáticamente
aplicando teoría de máximo y mínimo a la ecuación del momento ![]() .
.
![]()
![]() raíces
raíces 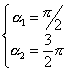
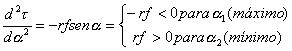
Calculemos ahora cual debe ser el módulo de la fuerza F para iniciar el ascenso de un escalón de altura h para un cilindro de masa m y radio R.
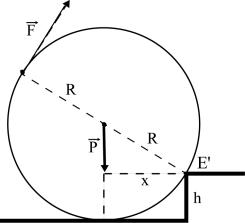
Fig. 3
![]()
![]()
![]() (1)
(1)
Finalmente calculemos la fuerza necesaria para iniciar el ascenso del escalón al cilindro, pero aplicando una fuerza horizontal en el punto superior del cilindro.
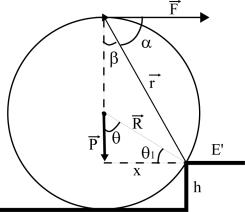
Fig. 4
Para iniciar el ascenso el momento de F respecto a E’ debe ser mayor que el del peso respecto al mismo punto.
En Fig. 4 indicamos con ![]() el vector
posición del punto de aplicación de
el vector
posición del punto de aplicación de ![]() y con
y con ![]() el de aplicación
del peso
el de aplicación
del peso ![]() . Ambos
respecto al mismo punto de referencia (E’).
. Ambos
respecto al mismo punto de referencia (E’).
![]() ,
, ![]()
![]()
En Fig. 4 se observa que ![]()
Por otra parte 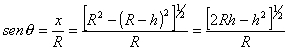
Reemplazando y despejando F, resulta
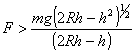 (2)
(2)
Comparando los resultados 1 y 2 se confirma el resultado inicial sobre donde aplicar la fuerza para obtener mas efecto.
PREGUNTAS
1) ¿Cuántos kilómetros ha viajado alrededor del sol desde que nació hasta el día de la fecha
2) ¿Puede un número de cualquier cantidad de cifras y terminado en 2, 3, 7 u 8 ser cuadrado de otro?
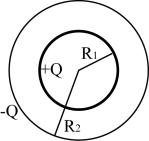
PROBLEMA
La figura muestra una sección de un capacitor esférico cargado. ¿Cómo varía el potencial desde r = 0 hasta r > R2.
Las ondas de presión que se propagan a lo largo de un tubo de longitud finita se reflejan en los extremos de manera muy semejante a como lo hacen las ondas transversales que viajan por una cuerda de extremos fijos.
La superposición de trenes de ondas que viajan en sentidos opuestos reflejados en los extremos del tubo originan ondas estacionarias, por las mismas razones y con las mismas características ya detalladas en el estudio de ondas estacionarias en cuerdas de extremos fijos.
La onda estacionaria se elongación tiene la misma forma que su equivalente transversal.
![]()
Y la onda estacionaria de presión, se obtiene de la anterior, pues
![]()
![]()
Comparando las ecuaciones se observa que los nodos de elongación, en una onda estacionaria longitudinal en un tubo, coinciden con los vientres de presión y recíprocamente los nodos de presión coinciden con los vientres de elongación.
La reflexión de la onda incidente en el extremo del tubo difiere según que sea abierto o cerrado. Cuando el tubo es cerrado el extremo coincide con un nodo de elongación, por lo tanto allí hay un máximo de presión.
Cuando el tubo es abierto el extremo coincide con un máximo de elongación, o sea un nodo de presión.
Nodo de elongación ![]()
Vientre de presión ![]()
Vientre de elongación ![]()
Nodo de presión ![]()
Fig. 1
En el caso del tubo cerrado, la reflexión se efectúa como en el caso de la cuerda de extremo fijo.
Si el extremo está abierto, la naturaleza de la reflexión
es más compleja y depende de la relación entre el tamaño de la abertura respecto
de la longitud de onda. Cuando el tubo es estrecho frente a ![]() , como sucede
en la mayor parte de los instrumentos de viento, la reflexión es tal que convierte
al extremo en un vientre de elongación, o sea un nodo de presión, esto se entiende
si tenemos en cuenta que en ese extremo el aire está a la presión atmosférica
y es de esperar que la presión allí sea constante.
, como sucede
en la mayor parte de los instrumentos de viento, la reflexión es tal que convierte
al extremo en un vientre de elongación, o sea un nodo de presión, esto se entiende
si tenemos en cuenta que en ese extremo el aire está a la presión atmosférica
y es de esperar que la presión allí sea constante.
Las ondas de elongación que se propagan en un tubo se reflejan en sus extremos del mismo modo que lo hace una onda transversal en el extremo fijo o libre de una cuerda.
Las reflexiones que se originan en la abertura donde es excitado el tubo son de tal naturaleza que se forma un vientre de elongación (nodo de presión) en la abertura o en sus proximidades.
La longitud efectiva de la columna de aire del tubo es un poco difícil de determinar exactamente.
Las vibraciones de las columnas de aire del tubo en los instrumentos de viento son generados por algún tipo de vibración que se produce en uno de los extremos: labios, caña, abertura, membranas, abertura con bisel, etc. En todos los casos, la columna de aire resuena con las componentes de Fourier que tienen frecuencias iguales a las de su sonido fundamental y sus armónicos.
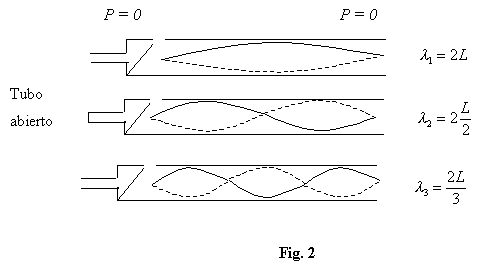
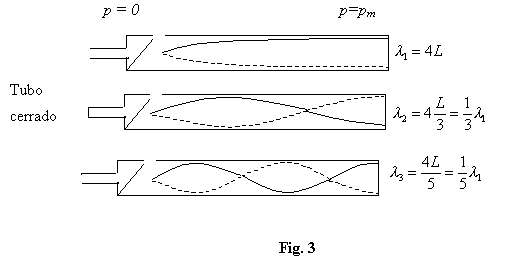
En las Fig. 2 y 3 se muestra para el caso de tubo abierto y tubo cerrado respectivamente, la onda estacionaria de presión para la frecuencia fundamental y los dos primeros supertonos.
Se observa que:
La frecuencia fundamental de un tubo abierto es el doble de la frecuencia fundamental de un tubo igual pero cerrado, o sea un tubo abierto resuena más agudo que otro cerrado. Se dice que su tono es una octava más alto.
Respecto de los supertonos, obsérvese que en el tubo abierto aparecen los armónicos de frecuencias múltiples pares e impares de la frecuencia fundamental, en cambio en el tubo cerrado sólo aparecen los armónicos de múltiplo impar de la fundamental, o sea:
“En un tubo abierto se pueden generar todos los armónicos del fundamental, en cambio en el tubo cerrado únicamente los armónicos impares”. Por lo tanto: dos tubos, uno abierto y el otro cerrado, de longitudes tales que tengan igual frecuencia fundamental, al vibrar diferirán en el timbre del sonido emitido.
Los resultados anteriores se pueden verificar cualitativamente mediante la construcción de un simple equipo.
Este esta constituido por una serie de tubos paralelos de igual diámetro pero de distintas longitudes. Su distribución se indica en Figura 4.
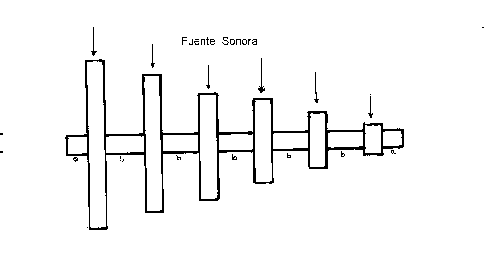
Fig. 4
La citada figura muestra una madera donde se han colocado en forma paralela 6 tubos .Ellos están separados por una distancia b ,que puede ser de unos 10 cm. Se deja en los extremos de la madera un espacio de unos 5 cm. para poder manipular al conjunto. Los tubos se pueden fijar a la tabla mediante una cinta adhesiva ancha ( las que se utilizan para embalaje).
Las longitudes recomendadas de los tubos son 15, 30, 45, 60, 75 y 90 cm. y de un diámetro aproximado de 5 cm.
Para utilizar este dispositivo es necesaria una fuente de sonidos puros o una mezcla. de ellos. Por ejemplo notas de instrumentos, música, ruido de la calle, etc.
Se puede fijar la madera base, horizontal o verticalmente, a un soporte y a una altura tal que los alumnos con comodidad puedan acercar sus oídos a los extremos de todos los tubos.
Para utilizar este dispositivo los extremos de un mismo lado deben enfrentar a la fuente sonora. El alumno acercara el oído a cada uno de los extremos del lado opuesto. y apreciara que los sonidos graves resuenan con mas intensidad en los tubos mas largos y recíprocamente para los sonidos agudos..
También podrá apreciar el cambio de resonancia cuando teniendo el oído próximo al extremo de un tubo (a una distancia de unos 5 cm), acerca su cabeza al extremo hasta taparlo con aquel. Con esta operación modifica el tubo de extremo abierto a extremo cerrado y, por lo tanto, cambia su frecuencia de resonancia.
RESPUESTAS A LOS PROBLEMAS DEL
NÚMERO ANTERIOR (11)
Enunciado
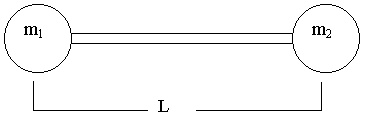
La figura muestra una pesa asimétrica. Ella consta de dos masas, m1 y m2 ,hechas de distintos materiales, pero igual radio y unidas por una varilla liviana.. Se verifica que m2 = 3 m1 .
Si se apoya verticalmente la pesa, primero sobre una masa y se deja caer y luego se repite la experiencia pero apoyando en la otra masa, se desea saber en que situación tarda menos tiempo la pesa en quedar horizontal. Sea L la distancia entre los centros de las esferas.
Resolución
Consideremos primero una situación similar a la del problema: una masa en la punta de una varilla muy liviana es mantenida verticalmente con la masa en el extremo superior. Nos preguntamos: con que aceleración rotará al dejarla caer ? (Ver figura)
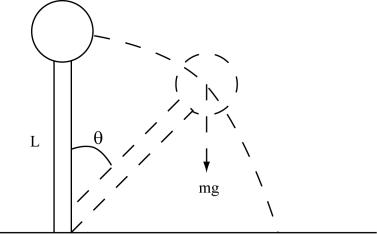
Por la segunda Ley de Newton aplicada a las rotaciones:
![]()
siendo ![]() el momento
de la fuerza peso respecto del punto de rotación, I el momento
de inercia respecto al mismo punto y
el momento
de la fuerza peso respecto del punto de rotación, I el momento
de inercia respecto al mismo punto y ![]() la aceleración
angular de la masa m.
la aceleración
angular de la masa m.
En este caso
![]() e
e ![]()
reemplazando y operando a = (g /LI)* sen q (1)
En esta deducción se ha supuesto que el centro de masa del sistema se encuentra en el centro de la masa m. O sea, la varilla tiene una masa despreciable frente a m.
De la ecuación (1) se concluye que: a) la aceleración no es constante, b) a mayor distancia del centro de masa al centro de rotación menor es la aceleración. Por lo tanto será menor la velocidad angular adquirida.
Esto explica por que es mas sencillo mantener en equilibrio verticalmente un escobillón con el cepillo en la parte superior y el extremo del mango apoyado en la palma de la mano y no al revés.
Para el caso del sistema del problema se debe calcular primero la distancia del centro de masa al centro de rotación. Aplicando la ecuación correspondiente se deduce que tal centro de masa se encuentra a (1/4) de la distancia que las separa a partir de la masa mayor ( y a 3/4 de la misma distancia respecto de la masa menor) .
Reemplazando esta distancias en la ecuación (1) resulta que :
a) cuando el sistema cae apoyado en la masa mayor
a = 4*(g / L) * sen q
b) cuando cae apoyado en la masa menor
a = (4/3 ) * ( g / L ) * sen q
Resumiendo cuando este sistema cae apoyado en la masa menor lo hace con una aceleración tres veces menor que en el caso opuesto.
Este resultado puede ser intuitivo, pero aquí tenemos la justificación analítica.
Enunciado
Un lápiz de longitud L está apoyado verticalmente sobre un espejo horizontal. Los rayos del sol inciden oblicuamente sobre dicho espejo, se reflejan y luego inciden sobre una pared blanca situada a una distancia D del lápiz.
Se desea saber si se notará la presencia del lápiz en la pared, en caso afirmativo con que forma y tamaño.
Resolución
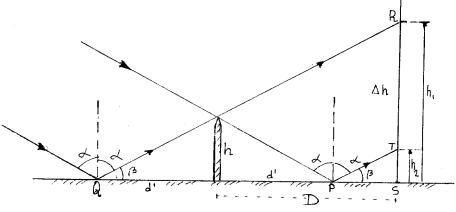
En la figura se supone que los rayos del sol inciden paralelos entre sí y con un ángulo de incidencia a.
De la figura se concluye:
![]()
![]() en
el triángulo QRS
en
el triángulo QRS ![]()
![]() en
el triángulo PTS
en
el triángulo PTS ![]()
![]()
![]()
El tamaño de la imagen es el doble que el del lápiz.
Observe que la pantalla puede acercarse hacia el lápiz hasta el punto P sin que se modifique el tamaño de la imagen.
Si se continúa acercando la pantalla, el tamaño de la imagen empezará a disminuir.
Se puede hacer una verificación experimental y cualitativa de este resultado.
No hace falta colocar un lápiz vertical sobre el espejo. Puede apoyar un segmento de madera o cartón en el espejo y verá en la pantalla y en la imagen del espejo (zona brillante) una zona oscura. Mida la longitud del objeto y de esa imagen y verificará los resultados anteriores
Enunciado
Explique utilizando conceptos físicos, porque es más cómodo dormir en un colchón mullido y tan incómodo en una cama de tablas, o sobre un piso plano y duro, sin colchón.
Resolución
Aquí lo que se debe analizar es la presión ejercida sobre la superficie en la que su cuerpo se apoya. En todas las situaciones la fuerza total ejercida y distribuida sobre tal superficie es la misma: su peso.
Lo que cambia es el área en que esta fuerza se aplica: a mayor superficie de contacto menor es la presión.
En un colchón que se deforma y se adapta a la forma de su cuerpo el área de contacto es máxima y, por lo tanto, mínima la presión. Su sensación de comodidad también es máxima.
Por el contrario si se acuesta en una superficie rígida, como el suelo o una cama de madera y sin colchón, la superficie de contacto disminuye , aumenta la presión y por lo tanto la incomodidad.
Enunciado
¿Porqué en noches frías de invierno es más frío cuando está despejado que cuando está nublado?
 |
La superficie de la tierra pierde calor por medio
de tres formas de transferencia,: por conducción, convección y radiación. Dos
de estas formas dependen de la diferencia de temperaturas, estas son: conducción
y convección, la primera es descripta por la ecuación D![]() donde k
es la conductividad térmica, A es el área de transferencia y DT/Dx el gradiente térmico, la segunda a través de la ecuación D
donde k
es la conductividad térmica, A es el área de transferencia y DT/Dx el gradiente térmico, la segunda a través de la ecuación D![]() donde h
es el coeficiente convectivo, A el área de transferencia y DT la diferencia de temperatura entre las áreas que intercambian calor.
En el intercambio radiativo la ecuación que lo rige es de la forma D
donde h
es el coeficiente convectivo, A el área de transferencia y DT la diferencia de temperatura entre las áreas que intercambian calor.
En el intercambio radiativo la ecuación que lo rige es de la forma D![]() donde s
es la llamada constante de Stefan-Boltzman (5,68x10-8
W/m2°K4),e es una propiedad de la superficie emisora conocida
como emisividad que tiene valores menores que 1. Vale 1 para un cuerpo negro
perfecto, y las T representan las temperaturas de la tierra y del cielo, respectivamente.
Se debe notar que éstas están a la 4ta. potencia .
donde s
es la llamada constante de Stefan-Boltzman (5,68x10-8
W/m2°K4),e es una propiedad de la superficie emisora conocida
como emisividad que tiene valores menores que 1. Vale 1 para un cuerpo negro
perfecto, y las T representan las temperaturas de la tierra y del cielo, respectivamente.
Se debe notar que éstas están a la 4ta. potencia .
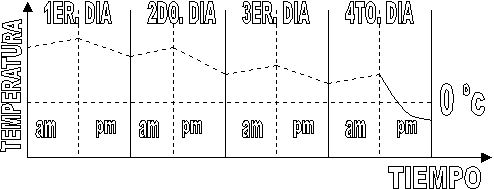
Veamos, para ejemplificar, una posible secuencia de sucesos . Para ello nos ayudaremos con la gráfica que se acompaña y que nos permitirá entender lo que pasa. Esta gráfica es nada mas que ilustrativa. Es a los efectos de entender el proceso y en la realidad puede tener diferentes formas. Estas secuencias, las que pueden ser con mas o menos días y también alternando cielos nublados con despejados y claros, guardan siempre similitud.
Se parte de un día cualquiera el cual esta nublado. Por consiguiente la temperatura inicial puede subir un poco o bien bajar durante las horas de sol pero en las horas de oscuridad caerá por debajo del valor inicial (influye también si esto ocurre en invierno cuando las horas de sol son menos que las sin sol). En esta etapa se intercambia calor con la atmósfera por conducción y convección, y fundamentalmente por radiación con la superficie inferior de las capas de nubes, las que se encuentran a temperaturas que están por encima del 0° C (valores típico de 8 °C a 20 °C). El segundo día el proceso se repite y la temperatura sigue bajando aunque lentamente. Si la humedad relativa es alta la sensación es de cierto confort. Este proceso con algunas variantes puede repetirse varios días mas. Al final del que hemos nombrado 4to día, el cielo se despeja completamente y el intercambio de calor por conducción y por convección se hace con la atmósfera. Estos procesos dependen del gradiente de temperatura. En cambio el proceso radiativo se hace ahora con un cielo despejado, cuya temperatura equivalente no es la de una nube de agua sino la de un gas que se encuentra, algunas veces, por debajo de los –50 °C (50 °C bajo cero). Este gas, además, es transparente a algunas bandas de emisión, fundamentalmente en el infrarrojo, por lo que, el intercambio de calor se hace ahora parcialmente entre la atmósfera y el medio interplanetario. Por lo tanto es mucho mayor la perdida de calor y la temperatura de la tierra baja bruscamente, por lo general por debajo de los 0°C, desencadenándose la helada.
De esta manera podemos explicar por que las noches despejadas son en general mas frías que las noches con cielo cubierto. El intercambio radiativo entre la superficie de la tierra , el gas que compone la atmósfera que tiene temperaturas por debajo de los 0°C como hemos dicho (se miden valores de 20 a 30 °C bajo cero) y el medio interplanetario (con temperaturas que pueden llegar hasta casi el cero absoluto –273,15 °C), tiene preponderancia frente a los otros procesos de intercambio de calor haciendo bajar la temperatura en mayor medida por depender de el factor de potencia 4.
Este tipo de procesos es usado en el campo de las energías alternativas para producir lo que se llama refrescamiento nocturno.
Enunciado
Una rueda de bicicleta rueda sin deslizar por un plano inclinado un ángulo a.
Se pide que encuentre una expresión que dé la velocidad del centro de masa de la rueda en función de la distancia L medida sobre el plano inclinado.
Se conoce la masa M de la cubierta, la llanta y los rayos, la masa m del eje de la rueda y el citado ángulo.
Resolución
Este problema puede ser resuelto aplicando las ecuaciones de la dinámica o considerando las variaciones de energía mecánica (cinética y potencial gravitatoria).
Al rodar la rueda por el plano inclinado no se realiza ningún trabajo de la fuerza de rozamiento, pues se supone que no hay deslizamiento. Por otr parte es necesario la existencia de un rozamiento entre la rueda y el plano, pues en caso contrario aquella deslizaría.
En consecuencia el incremento de energía cinética de la rueda a medida que desciende, se obtiene de una disminución de la energía potencial gravitatoria.
La energía cinética en un instante dado del movimiento está constituida por la de traslación y la de rotación, ambas referidas al centro de masa (cm):
![]()
Además ![]() (R: radio
de la rueda) e I=mR2
(R: radio
de la rueda) e I=mR2
Reemplazando: ![]()
![]()
![]() (1)
(1)
Después de recorrer una distancia L sobre el plano, la masa ha descendido una altura:
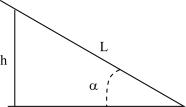
h = L sen a
Por lo tanto su energía potencial ha variado en
![]()
Si partió del reposo la expresión (1) da la variación de energía cinética, por lo dicho al principio.
![]()
de donde 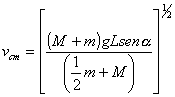
NOTICIA
Se informa a los lectores e interesados que el presente número de esta Revista y algunos anteriores están a su disposición en la página web de la Universidad Nacional de San Luis. http://bib0.unsl.edu.ar/bibls/publ-online.html
Para consultas, sugerencias, etc., puede hacerlo por correo electrónico:
Email: cmaga@unsl.edu.ar
Editor: El Profesor de Ciencias, Departamento de Física,
Univ. Nac. de San Luis. C.C. 136 – CP: 5700 – San Luis