
EL PROFESOR
DE
CIENCIAS
Número 11 DICIEMBRE/99
Facultad de Ciencias Físico Matemáticas y Naturales
Universidad Nacional de San Luis
OBJETIVOS
Esta publicación está destinada a Profesores de Nivel Medio en Matemáticas y Física.
El objetivo fundamental es establecer una comunicación directa de la Facultad de Ciencias Físico Matemáticas y Naturales (UNSL) con dichos Profesores, a efectos de desarrollar actividades que permitan mejorar la calidad de su enseñanza en estas ciencias y, por lo tanto, mejorar la calidad de sus egresados.
El contenido de esta publicación estará constituido por artículos metodológicos e instrumentales para la enseñanza teórica y práctica de temas del currículum de nivel medio, problemas y su metodología de resolución, desarrollo de temas de actualidad en relación a su aplicación al currículum, prácticos de laboratorio, preguntas y respuestas para transferencia de conocimientos, noticias de carácter educativo en el área, evaluación, cartas, comentarios y artículos enviados por los docentes-lectores, donde puedan aportar, solicitar o compartir sus logros, necesidades, dudas y, finalmente todo artículo cuyo contenido los profesores soliciten, sugieran o sea oportuno incluir.
Señor Profesor:
Para lograr el propósito de mantener la edición de esta publicación, se necesita de la respuesta y colaboración de los destinatarios. Esto significa que es muy necesario, y se lo agradecemos desde ya, nos haga llegar sus opiniones, solicite y aplique el material que le ofrecemos, envíe artículos para publicar y difunda esta pequeña revista.
Muchas Gracias
INDICE
Publicación subsidiada por la Facultad de Ciencias Físico Matemáticas y Naturales de la Universidad Nacional de San Luis
IDEA Y REALIZACION: Lic. Carlos Magallanes
HTML Y Publicación Web: Prof. Germán Roque Arias
1) En lo posible evitar leer el problema. Esto genera perdida de tiempo y confusión.
2) Si la presión del Profesor lo impone, leerlo, pero sin preocuparse por entender el significado del enunciado.
3) A lo mas concentrar la atención en los números y utilizarlos en el orden en que aparecen en el enunciado.
4) Si el problema pregunta por una cantidad esto significa que hace falta una fórmula. En caso contrario, faltan datos.
5) La fórmula a aplicar debe tener tantas letras como datos tiene el problema.
6) Una vez que la calculadora hizo el trabajo de sacar las cuentas , copiar el número que indica y, a veces, agregar las unidades de la magnitud que pide el problema.
7) Si eventualmente el alumno repara que el número que da el resultado es exageradamente chico o grande para lo que se pregunta, no preocuparse. La culpa la debe tener la calculadora o el profesor.
Levantar objetos es una actividad casi permanente en la vida diaria, ya sea en el trabajo, el hogar o el deporte.
Generalmente pese a las indicaciones y consejos médicos esta acción se efectúa incorrectamente.
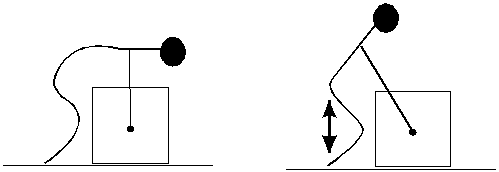
Los médicos aconsejan: para levantar un objeto pesado flexionar las rodillas y descender el tronco del cuerpo hasta que las manos alcancen el objeto. Luego haciendo fuerza con las piernas eleve el tronco y el cuerpo hasta la altura deseada.
a b
Sin embargo, lo más probable es que cometamos el error de flexionar la espalda, agacharnos y desde esa posición levantar el cuerpo (parte a figura 1)
Esta acción incorrecta puede generar lesiones en los discos lumbares que traen serias y dolorosas consecuencias: las hernias de disco.
El disco es un tejido esponjoso que se encuentra entre las vértebras de la columna. Su función es amortiguar la transmisión de golpes a lo largo de la columna y permitir su rotación y flexión.
A medida que transcurre la edad de la persona va perdiendo su contenido de agua lo que la hace frágil y quebradizo.
Cuando se fractura este disco por alguna acción mecánica exterior , toca el nervio ciático, el que se encuentra dentro de la columna, generando fuertes e insoportables dolores.
En este articulo se pretende mostrar como la acción de levantar un peso en forma incorrecta puede generar la hernia de disco de la zona lumbar de la columna.
Dividamos el cuerpo humano en dos partes: la base, desde los pies hasta la quinta vértebra lumbar y, el tronco, desde allí hasta la cabeza.
Cuando hacemos una flexión del tronco hacia adelante y luego lo levantamos hasta la vertical, la rotación se efectúa respecto de un eje imaginario que pasa por la cintura ( quinta vértebra lumbar).
La acción de levantar el torso es efectuada por un conjunto de músculos distribuidos a lo largo y a lo ancho de la espalda. Representaremos en forma simplificada el cuerpo humano de la forma mostrada en figura 2.
La barra vertical representa las piernas y la horizontal el torso desde la cintura hasta la cabeza.
En dicha figura se representa con P el peso del torso y la cabeza, con Pc el peso del cuerpo a levantar, con F la fuerza de los músculos espinales de la espalda y con R la reacción del sacro sobre la columna lumbar.
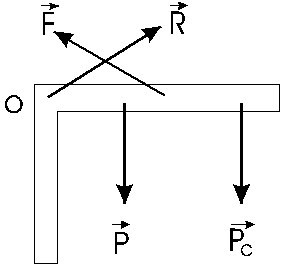
La fuerza F es ejercida por la contracción de los músculos espinales. El ángulo que ella forma con la dirección de la columna es del orden de 12 grados. Por lo tanto tiene una gran componente en dirección de esta . Esta componente es la que presiona sobre los discos intervertebrales, llegando , si el esfuerzo es muy grande, a herniarlos.
Analizaremos un ejemplo concreto para ilustra mejor la relación entre el peso levantado y el valor de F.
Partamos de la situación de una persona flexionada con la espalda horizontal y que se mantiene estático en esa posición . (Figura 2) .La columna puede girar respecto de un eje que pasa por el punto O de la figura.
Indiquemos con h la distancia desde el sacro hasta los hombros. De acuerdo a las tablas antropométricas el peso del torso, en promedio es el 60% del peso de la persona, y su centro de gravedad se encuentra a 0,6 h. La fuerza resultante muscular F se encuentra a 0,7 h.
Como el torso esta en una posición estática podemos aplicar las condiciones de equilibrio, es decir :
S Fi = 0 y S Mi = 0 (1)
Esto significa que la suma de las fuerzas que actúan sobre el sistema en estudio (el torso) y la suma de los momentos respecto de un punto se anulan.
En figura3 se muestran las componentes de las fuerzas representadas en figura 2 (sin Pc ). Se han tomado dos direcciones : x según la columna e y vertical para descomponer tales fuerzas.
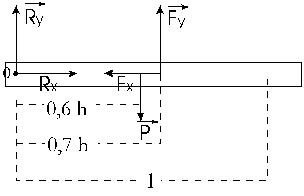
Si la masa de la persona es de 100 kg, entonces (en números redondos)
P =600 N.
Aplicando las ecuaciones (1) resulta:
M0: Fy . 0,7 h – P . 0,6 h = 0 (4)
Resulta: Fy = 514 Nt,
F = Fy / sen 12º à F = 2472 Nt, Fx = 2418 Nt
Ry = 86 Nt, Rx = 2418 Nt
Obsérvese que la fuerza que ejercen los músculos de la espalda de esta persona para mantenerla horizontal es del orden de 4 veces mayor que el peso del torso.
Si ahora agregamos que la persona tiene levantado un peso (200 Nt), veamos que sucede con la fuerza calculada en el ejemplo anterior.
Eje y: Ry + Fy – P – Pc = 0
M0: Fy – 0,7 h – P . 0,6 h – Pc h= 0
resultando
Fy = 800 Nt, Fx = 3763 Nt, F = 4535 Nt, Rx = 3763 N, Ry = 0
Obsérvese que la componente de F en dirección de la columna es del orden de 18 veces mayor que el peso levantado (casi 5 veces si se incluye el torso)
Este problema, mas allá de la oportunidad de aplicar las condiciones de equilibrio estático, sirve para que el alumno adquiera conocimiento sobre su cuerpo y como trabajan algunos de sus músculos, cuales son sus limitaciones y peligros de su mal uso. Es saludable y útil recalcar este aspecto para una vida mejor.
La figura muestra una pesa asimétrica. Ella consta de dos masas, m1 y m2 ,hechas de distintos materiales, pero igual radio y unidas por una varilla liviana.. Se verifica que m2 = 3 m1 .
Si se apoya verticalmente la pesa, primero sobre una masa y se deja caer y luego se repite la experiencia pero apoyando en la otra masa, se desea saber en que situación tarda menos tiempo la pesa en quedar horizontal . Sea L la distancia entre los centros de las esferas.
 |
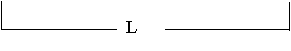 |
Para el tema Leyes de Newton se relaciona la fuerza con la aceleración (Ley de masas), la Ley de acción y reacción y la Ley de Inercia..
Si bien abundan ejemplos en el mundo real, en la mayoría no es fácil “ver” la acción y la reacción y otros no despiertan el interés de los alumnos. Por eso es importante que en la búsqueda de ejemplos, estos sean sencillos o estén vinculados a la vida diaria del joven. En los deportes hay una fuente de ejemplos motivantes.
En este articulo se propone el análisis de la acción del viento sobre la vela de una tabla de windsurf.
El “windsurfista” tiene la posibilidad de hacer girar la vela respecto de un eje vertical (mástil) de tal modo que la pueda orientar hacia una posición tal que el viento incide por atrás en una dirección oblicua.
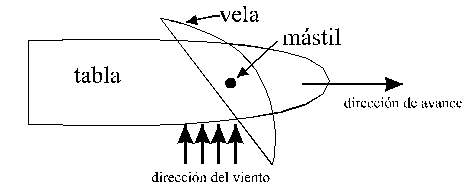
De acuerdo al grafico la tabla debería derivar en la dirección del viento. Sin embargo avanza en otra dirección, por ejemplo la que indica la figura 1.
¿Cómo se explica esto?
En un esquema simplificado en figura 2 se indica con T una vista desde arriba de la vela. También se indican:
Fv = la fuerza aplicada por el viento en un punto P de la vela.
V = el viento se refleja en P
Fvr = por reacción actúa sobre la vela una fuerza opuesta
Fres.= fuerza resultante de las dos fuerzas que actúan sobre la vela Fv y Fvr
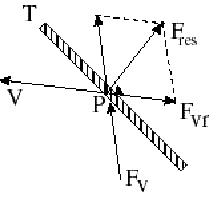
Figura 2
De acuerdo al gráfico la tabla debería moverse en dirección de Fres, sin embargo debe tenerse en cuenta que la tabla esta en contacto con el agua la cual ofrece una fuerza resistente al desplazamiento en cualquier dirección. Esta fuerza resistente es aumentada en dirección transversal por la quilla que lleva la tabla sumergida en su parte inferior.
En un diagrama simplificado en figura 3 se muestra Fres y la fuerza resistente Fa. También se indica la resultante de estas dos fuerzas: Fff.
Se observa que la fuerza final que actúa sobre la tabla: F ff es la que da su dirección de avance. Su dirección depende de Fres .Esta dirección la regula el deportista girando la orientación de la vela respecto a la del viento y así logra el avance en la dirección deseada.
Se sugiere la implementación de este ejemplo mediante un carrito de laboratorio al cual se le puede agregar un mástil con una vela de papel, cuyo plano forme un ángulo que se pueda variar con respecto al eje longitudinal del carrito. Para obtener el viento se puede utilizar un ventilador de baja velocidad.
La superficie sobre la que coloque el carrito debe ser áspera para proporcionar la fuerza de arrastre (Fa ) y evitar el deslizamiento del carrito en la dirección del viento.
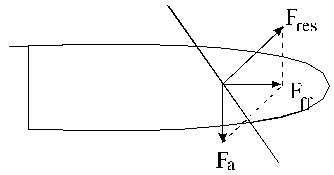
Figura 3
Pregunta
Un lápiz de longitud L está apoyado verticalmente sobre un espejo horizontal. Los rayos del sol inciden oblicuamente sobre dicho espejo, se reflejan y luego inciden sobre una pared blanca situada a una distancia D del lápiz.
Se desea saber si se notará la presencia del lápiz en la pared, en caso afirmativo con que forma y tamaño.
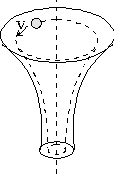
Obtenga un embudo de plástico mediano ( diámetro aproximado 20 a 30 cm) y una bolita de vidrio.
Coloque el embudo en posición vertical y tomándolo por la parte inferior con movimientos circulares lentos y de pequeño diámetro ensaye hasta lograr que la bolita se mueva en círculos cerca del borde superior del embudo. (ver figura).
Ensaye hasta lograr mantenerla en movimiento circular uniforme en una órbita circular plana de radio constante
La propuesta es analizar que fuerzas actúan sobre la bolita, cuales son sus direcciones y magnitudes. Todo en base a sencillas mediciones.
Sugerencias: recuerde que cuando un móvil efectúa un movimiento circular uniforme es necesario que sobre él actúe una fuerza centrípeta.
La otra fuerza que actúa sobre la bolita es su peso.
No olvide la normal.
Si dispone de un cronometro y de una balanza puede estimar la fuerza centrípeta midiendo la masa de la esfera y el periodo del movimiento circular.
También puede determinar la normal midiendo la inclinación de la pared del embudo. Luego obtener la resultante entre peso y normal, relacionar y comparar resultados.
Pregunta
Explique utilizando conceptos físicos, porque es más cómodo dormir en un colchón mullido y tan incómodo en una cama de tablas, o sobre un piso plano y duro, sin colchón.
Si tiene acceso a una balanza electrónica (como la que usan en el supermercado) puede hacer una sencilla y rápida aplicación y/ o verificación del Principio de Arquímedes.
El objetivo es determinar el volumen de un cuerpo de forma irregular.
El material necesario es la balanza electrónica, un vaso de precipitación de un tamaño que permita introducir el cuerpo y mantenerlo sumergido sin apoyarlo, agua y un calibre para medir longitudes.
Coloque el vaso de precipitación con agua sobre la balanza. La cantidad de agua la debe estimar teniendo en cuenta que no vuelque cuando se sumerja el cuerpo. Anote el peso del sistema vaso + agua.
Colgando el cuerpo de un hilo sumérjalo en el agua hasta cubrirlo totalmente y sin que apoye en el fondo.
La balanza indicara un peso mayor que el anterior. Tome nota de él.
¿Cómo se determina el volumen?
E = Vc .dagua. g (1)
Vc es el volumen del cuerpo sumergido, luego están la densidad del agua y la aceleración gravitatoria g.
Al empuje sobre el cuerpo este responde, por acción y reacción, con una fuerza igual y opuesta.
Esto se observa en que la balanza indica un peso mayor y sin que el cuerpo se haya apoyado en el fondo. Este valor es el peso anterior más el empuje: P0 + E..
Para que los alumnos confíen en el experimento se sugiere una experiencia previa.
Ella consiste en medir el volumen de un cuerpo por otro camino. Para este fin lo mas apropiado es utilizar una esfera de un material que asegure que se puede sumergir y que no flotara (Empuje menor que el peso).
Con el calibre se puede tomar un valor promedio de su diámetro y luego determinar su volumen. Este resultado se debe contrastar con el obtenido con el empuje según la descripción anterior. La diferencia entre los valores obtenidos puede dar una idea del error relativo en la determinación del volumen por este método, tomando como referencia el valor obtenido por medición directa del diámetro.
Es importante recalcar ante los alumnos la importancia de la operación de determinar o estimar el error cometido en un experimento para que incorporen la idea de que toda medición implica la existencia de un error.
Los campos eléctricos y magnéticos manifiestan su presencia por la acción eléctrica o magnética sobre cuerpos con cargas eléctricas o magnetizados, respectivamente.
Por otra parte las corrientes eléctricas generan campos magnéticos en el espacio que las rodea.
Esta sugerencia experimental tiene por objetivo mostrar la sencillez con que se puede hacer una rápida demostración de la existencia de estos campos. Por supuesto es conveniente hacerla antes de analizar el tema con los alumnos.
El material necesario es: a) dos pares de pajitas de bebidas, b)una caja de cartón de tamaño regular, c) dos imanes pequeños (por ejemplo de puerta de heladera), d) dos bobinas circulares de alambre de cobre de unos 5 cm de diámetro, e) dos pilas, alfileres y cables.
Operaciones previas
1) En la caja quite la tapa y dos costados opuestos, dejando aquellos que tengan una longitud mayor que la de las pajitas.
2) Arme las bobinas, para ello enrolle 10 o más vueltas de alambre fino y esmaltado de cobre en un cuerpo de forma cilíndrica de unos 5 cm de diámetro.
3) Arme los péndulos con dos pajitas pinchadas con un alfiler (ver figura 1)
4) Pegue con plastilina, en el extremo opuesto a la pajita vertical, un trozo pequeño de imán (ver figura 2)
5) Suspenda el péndulo con los imanes en los bordes de la caja (figura 3).
6) Acerque los péndulos desplazando las pajitas horizontales que están apoyadas en los bordes superiores de la caja.
7) Observara repulsión o atracción entre los imanes. Invierta uno de ellos y observara el efecto opuesto.
Este resultado no es novedad para los alumnos pues ellos, seguramente saben de la atracción o repulsión entre imanes según que polo se enfrente. El objetivo de esta parte del experimento es mostrar que el dispositivo sirve para detectar la interacción entre campos magnéticos.
8) Sustituya uno de los imanes por una bobina. Conecte los cables como indica la figura 4
9) Coloque los péndulos separados por una pequeña distancia.
10) Conecte brevemente los cables que están unidos a la bobinita y a los bornes de la pila. Si la disposición es la correcta deberá observar una atracción o repulsión entre bobina e imán.
11) Invierta la conexión de la pila para hacer circular la corriente por la bobina en sentido contrario al anterior.
En este momento debe cuidar que los alumnos concluyan que cuando circula corriente por la bobina se produce una interacción entre esta y el imán igual que en caso de los imanes entre sí.
12) Sustituya el imán por la otra bobina y coloque los péndulos cercanos entre sí como en la situación anterior. Cuide el paralelismo de las bobinas.
13) Con la ayuda de un alumno haga conexiones breves y simultaneas de los cables de las bobinas a las respectivas pilas.
14) Repita el paso anterior pero invirtiendo el sentido de la corriente en una de las bobinas.
Si la experiencia está correctamente realizada deberá observar una atracción entre las bobinas en un paso y una repulsión en el otro.
Que la conexión sea breve es a los efectos de no agotar la pila pues esta, está trabajando prácticamente en cortocircuito.
Esta experiencia debe convencer a los alumnos que cuando circula una corriente por un conductor aparece un efecto de características magnéticas y que es importante el sentido en que circula dicha corriente.
Una fuerte recomendación es que este experimento debe ser ensayado antes de ser presentado ante los alumnos. La razón está en que hay varios parámetros a controlar y balancear y que intervienen en el experimento tales como numero de vueltas e intensidad de la corriente por las bobinas, peso de los imanes y de las bobinas, etc.
Una observación final es que esta sugerencia esta abierta a otras posibilidades, por ejemplo en lugar de bobinas circulares pueden ser rectangulares o se puede utilizar la idea para mostrar fuerzas entre conductores rectilíneos paralelos con corrientes de igual u opuesto sentido.
El final de la sugerencia es que si el Profesor tiene la oportunidad y los alumnos están dispuestos a colaborar puede encargar a un grupo de ellos a que realicen la demostración a sus compañeros.
Independientemente de quien realice la demostración una cosa es segura: no costara esfuerzo convencer a los alumnos que las ecuaciones correspondientes que el profesor plantea en la pizarra responden a la realidad física.
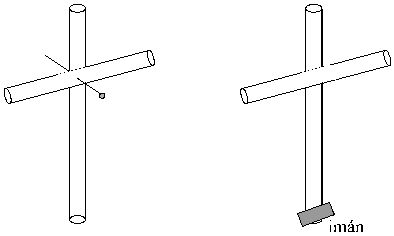
Fig. 1 Fig 2
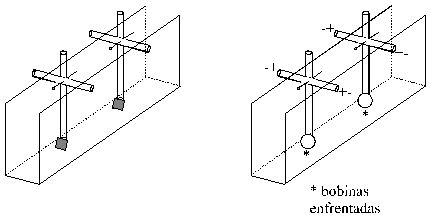
Fig. 3
El concepto de potencia suele desarrollarse en el aula de física en forma teórica y aplicada a problemas generalmente alejados de la realidad de los alumnos.
¿Por qué no medir la potencia de un pequeño motor de un grabador, de una bandeja giradiscos, de un juguete etc.? Estos motores son de bajo costo y se suelen encontrar descartados en los talleres de electrónica o en el cajón de los juguetes del hermanito.
La implementación de la experiencia es muy sencilla. Solo basta fijar el motor a una madera y esta con una prensa al borde de una mesa del aula o laboratorio. También será necesario una batería o fuente de corriente continua para hacer funcionar el motor.
Recuerde que la fuente o las pilas deben ser del voltaje que corresponde al motor.
También necesitara un voltímetro y un miliamperímetro.
Corte un trozo de cinta de grabador de un casete en desuso. La longitud de la cinta debe ser menor que la distancia que hay del motor al piso una vez fijado a la mesa de trabajo.
Haga dos marcas en la cinta separadas por una distancia d que deberá medir antes de la experiencia.
Adhiera la cinta de grabador al eje del motor y cuelgue del extremo libre una pesa, que llamaremos p.
La pesa p debe quedar colgando y la cinta colocada de tal modo que al funcionar el motor se vaya enroscando en el eje y sobre si misma.
Verifique que la cinta no se ha estirado a causa de que la pesa p está colgando. Mida nuevamente en esa situación d.
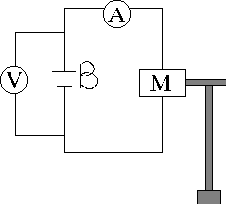
Conecte en paralelo con la fuente el voltímetro y en serie el miliamperímetro.
Durante la experiencia se deberá tomar nota del voltaje entre los bornes del motor cuando esta trabajando y de la corriente que circula por el circuito. Simultáneamente se deberá medir el tiempo en que el motor levanta la pesa p la distancia d marcada en la cinta.
Para elegir la pesa p apropiada al motor elegido se deberán hacer ensayos previos para asegurar que el motor trabaje en el régimen de esfuerzo para el cual ha sido diseñado.
Cuando el motor trabaje en este régimen el voltaje y la corriente permanecerán constantes durante la experiencia.
La potencia liberada por el motor P = V.I
Esta potencia fue utilizada para levantar la pesita p la altura d en el tiempo t medido.
Esta potencia esta medida también por P = W/t = mgd/t.
Los valores obtenidos por ambas ecuaciones deben ser cercanos en razón de los errores experimentales en la determinación de las magnitudes utilizadas. Además hay un trabajo de las fuerzas de rozamiento y la deformación de la cinta que no es posible determinar en forma directa.
Una diferencia no mayor al 10 % es un criterio razonable para considerar bien hecha la experiencia. Por supuesto se debe procurar minimizar esta diferencia. Si se obtienen valores iguales no es una experiencia, tal vez sea una coincidencia.
Figura
Pregunta
¿Porqué en noches frías de invierno es más frío cuando está despejado que cuando está nublado?
PROBLEMA
Una rueda de bicicleta rueda sin deslizar por un plano inclinado un angulo a.
Se pide que encuentre una expresión que dé la velocidad del centro de masa de la rueda en función de la distancia L medida sobre el plano inclinado.
Se conoce la masa M de la cubierta, la llanta y los rayos, la masa m del eje de la rueda y el citado ángulo.
Aportes para la enseñanza de la Geometría
Poliamantes
Hace más de 30 años, el matemático norteamericano Salomón Golomb acuño el término Poliominó para describir a cualquier figura plana formada uniendo cuadrados de igual tamaño por los lados.
En el libro de Golomb (no pudimos conseguirlo) se sugiere la posibilidad de utilizar triángulos de manera similar.
Tomas O'Beirne, recogió la idea y pensando que si dos triángulos equiláteros unidos por un lado forman el diamante de la baraja francesa, el nombre genérico de este tipo de figuras debía ser Poliamantes.
¿Cuántas piezas diferentes pueden obtenerse uniendo triángulos equiláteros?
Hay un Diamante, un Triamante, tres Tetramantes, cuatro Pentamantes y doce Hexamantes.
Los Poliamantes son un juego abierto.
El campo para investigar no tiene límites.
Nuevamente con Uds. queridos profesores para contarles la continuación de esta apasionante experiencia didáctica iniciada en el número anterior.
Los alumnos se plantearon los siguientes objetivos e hipótesis.
Ø Aprender a investigar
Ø Jugar.
Ø Participar de la Feria de Ciencias.
Ø Construir un grupo trabajando.
Ø Enseñarle a la comunidad que se puede aprender a través del juego.
Los Poliamantes producen cubrimiento.
Se transcribe la experiencia.
Hace más de 30 años, el matemático norteamericano Salomón Golomb acuño el término Poliominó para describir a cualquier figura plana formada uniendo cuadrados de igual tamaño por los lados.
En el libro de Golomb (no pudimos conseguirlo) se sugiere la posibilidad de utilizar triángulos de manera similar.
Thomas O'Beirne, el matemático que tenía a su cargo la sección de recreaciones de la revista “New Scientist” recogió la idea.
Siguiendo el camino trazado por Golomb, razonó que si dos triángulos equiláteros unidos por un lado forman el diamante de la baraja francesa, el nombre genérico de este tipo de figura debería ser “Poliamantes”.
Tanto los Poliominós como los Poliamantes son figuras reversibles. Esto es, si en vez de figuras dibujadas en el papel se los considera fichas, se los puede rotar o levantar de la mesa, darla vuelta en el aire y volver a apoyar. Es decir, una pieza y su imagen especular son iguales.
En estas condiciones nos pusimos a ver ¿Cuántas piezas diferentes se pueden obtener uniendo triángulos equiláteros?
![]() Hay un diamante:
Hay un diamante:
Hay solamente un Triamante
¿Y con cuatro triángulos equiláteros?
Hay tres Tetramantes
¿Y con cinco triángulos equiláteros?
Hay cuatro Pentamantes.
¿Y con Seis, o sea Hexamantes?
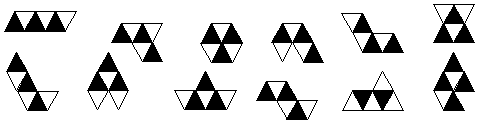 |
Hay doce Hexamantes
Por una curiosa coincidencia, hay doce Hexamantes, la misma cantidad que Pentominós.
Aquí nos empezamos a preguntar sobre si estas figuras producen cubrimientos.
Empezamos con los doce Hexamantes, que tienen en total 12 x 6 = 72 Triángulos.
En otras palabras, los doce Hexamantes cubren una superficie de 72 Triángulos; pero ¿Que forma debe tener tal superficie?
Empezamos con un anillo en forma triangular formado por 72 triángulos.

Al comienzo todo parecía un juego, pero no podíamos lograrlo. Rosita nos sugirió pensar las piezas pintadas como si fuese un tablero de ajedrez de casillas triangulares.
Las diez primeras piezas tienen cada una tres casillas claras y tres oscuras, las dos últimas tienen cuatro casillas de un tipo y dos del otro.
Es evidente que según como se las coloque sobre el tablero, las cuatro casillas iguales podrán ser de uno u otro color.
Entonces la figura a recubrir por los Hexamantes deberá pertenecer a uno de dos tipos:
1. Aquellas que al ser pintadas como las casillas de ajedrez tengan la mitad de las casillas de un color y la otra mitad del otro. Entonces las dos últimas piezas deberán estar ubicadas de manera que el exceso de casillas de un color de una se compense con los de la otra.
2. Aquellas que al ser pintadas como se indica tengan exactamente cuatro casillas más de un color que del otro. Entonces las dos últimas piezas se ubicarán de modo que en ambas coincida el color de las cuatro casillas de igual tono.
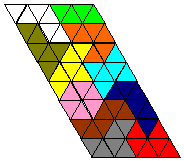 |
|||||
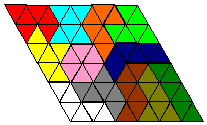 |
|||||
 |
|||||
Es fácil ver que el anillo triangular tiene 39 casillas de un color y 33 del otro, por lo tanto es imposible cubrirlo con los doce Hexamantes.
Aquí estábamos un poco desanimados ¡Hernán quería abandonar todo!, Pero nuestra asesora nos sugirió probar con figuras más simples, y así empezamos con el rombo de 6 x 6 y luego con el rombo de 4 x 9 y encontramos soluciones para ellos.
 |
Para el rombo de lado 3 x 12 en cambio no pudimos encontrar una solución.
A pesar que cumple la condición 1, no pudimos lograr un cubrimiento.
Las condiciones 1 ó 2 son, sin embargo, sólo condiciones necesarias pero no suficientes.
Si una figura cumple con alguna de ellas hay una sola forma de saber si es posible cubrirla: haciéndolo.
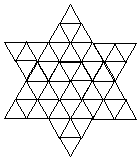 Un poco más fuertes después de lograr algunos cubrimientos nos pusimos
a cubrir una estrella como la figura:
Un poco más fuertes después de lograr algunos cubrimientos nos pusimos
a cubrir una estrella como la figura:
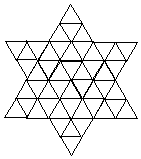 |
Esta estrella se cubre con 8 Hexamantes.
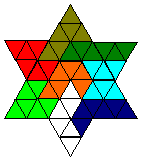 |
A pesar que trabajamos mucho, no pudimos lograr otro cubrimiento, hasta ahora.
¿Se podrán crear juegos con otros Poliamantes?
El campo para investigar no tiene límites.
1. Hay un Diamante.
2. Hay un Triamante.
3. Hay tres Tetramantes.
4. Hay cuatro Pentamantes.
5. Hay doce Hexamantes.
6. Algunos Poliamantes producen cubrimientos.
7. No puede cubrirse con los doce Hexamantes el anillo triangular formado por 72 triángulos.
8. Puede cubrirse con los doce Hexamantes un rombo de 6 x 6.
9. Con ocho Hexamantes se puede cubrir una estrella de seis puntas.
10. Puede cubrirse con los doce Hexamantes un rombo de 4 x 9.
11. No puede cubrirse con los doce Hexamantes un rombo de 3 x 12.
1. Revistas acertijo.
2. Matemática 7º E. G. B. 3 _ Gustavo Barallobres. Editorial Aique _ 1997
3. Matemática 8º E. G. B. 3 _ Mirta Hanfling. Editorial Aique _ 1998
EL PROBLEMA DE LA CAPA DE OZONO
El planeta Tierra, como los otros planetas del sistema solar, recibe radiaciones procedentes de numerosos lugares del universo (sol, estrellas, galaxias, etc.).
La fracción de energía radiante que llega a la Tierra que procede del Sol es la de mayor valor respecto de las otras. Su intensidad es tal que hace despreciable a las restantes. Por eso el estudio de la naturaleza, intensidad, y otras características de la radiación solar ocupa un lugar importante en la Ciencia de nuestros días.
Una parte importante de esta radiación llega a la superficie terrestre, el resto se atenúa en las capas superiores de la atmósfera.
La radiación que llega a la superficie está constituida principalmente por la infrarroja (ondas electromagnéticas de longitudes de onda entre 0.1 a 1000 mm aproximadamente). y la luminosa (ondas electromagnéticas de longitudes de onda entre 0.39 a 0.77 mmetros). La primera la percibimos por la sensación térmica sobre nuestro cuerpo o la variación de temperatura sobre los otros y la segunda por el sentido de la vista. También hay radiaciones de otras frecuencias que no son percibidas por nuestros sentidos. Entre ellas, la más importante es la radiación ultravioleta (ondas electromagnéticas de longitud de onda entre 0.1 y 0.001 mm).
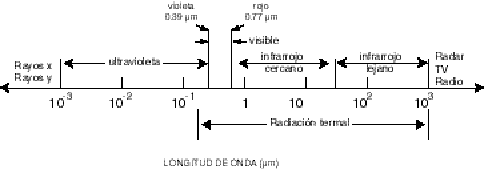
violeta 0.390 – 0.455 µm
azul 0.455 – 0.492 µm
verde 0.492 – 0.577 µm
amarillo 0.577 – 0.597 µm
naranja 0.597 – 0.622 µm
rojo 0.622 – 0.770 µm
El espectro ultravioleta puede ser dividido en tres bandas:
uv cercano 0.3 – 0.4 µm
uv lejano 0.2 – 0.3 µm
uv máximo 0.001 – 0.2 µm
Afortunadamente hay radiación ultravioleta que no llega a la superficie terrestre. De hacerlo, a causa de su alta energía y por lo tanto alto poder ionizante, produciría efectos dañinos sobre la vida animal y vegetal.
La razón de que estas radiaciones no lleguen a nosotros se encuentra en la acción de filtro que sobre ellas efectúan las capas superiores de la atmósfera.
Uno de los componentes que se encuentra en la atmósfera y que actúa en esta acción de filtro es el ozono.
El ozono es un gas constituido por moléculas formadas por tres átomos de oxigeno (O3). El oxigeno (O) tiende a formar moléculas diatómicas a causa de su alta electronegatividad.
Para formar una molécula de ozono ( O3 ) hace falta agregar a una de oxigeno molecular ( O2 ), un átomo de oxigeno ( O ). Recíprocamente de una molécula de ozono se puede obtener un átomo de O y una molécula de O2 . En ambos procesos hace falta una energía. Esta energía es provista por la radiación ultravioleta.
Para que la atmósfera actúe como filtro de las radiaciones ultravioletas dañinas para la vida terrestre debe tener una concentración suficiente de O3.
A causa de que esta concentración esta disminuyendo, y por lo tanto las radiaciones dañinas están alcanzando la superficie terrestre y la vida sobre ella, es que hoy día el problema de la reducción del espesor de la capa de ozono es de importante y preocupante actualidad.
No escapará al criterio del Profesor-lector que este problema es de todos, tanto como afectados y como, según se estima, cómplice pasivo del origen del mismo.
Teniendo en cuenta la oportunidad y obligación del Profesor de concientizar a sus alumnos para asumir una actitud de defensa del medio ambiente, capa de ozono incluida, este articulo pretende aportarle información mínima sobre el citado problema y con la intención de estimular su responsabilidad y así lograr que adquiera mayor información y la transmita a sus alumnos. Tenga en cuenta que ellos y sus hijos serán los herederos y afectados por este problema si no se resuelve o detiene.
El ozono se encuentra en la atmósfera en distintas concentraciones según la altura.
A baja altura ( nivel del mar) la concentración es mínima. La máxima se encuentra, en promedio, entre 20 y 25 km en la llamada capa de ozono. La latitud es otra variable a tener en cuenta, en los polos aumenta la concentración.
A nivel del mar y en condiciones normales el aire atmosférico esta constituido en un 80% por nitrógeno, en un 19% por Oxígeno y el resto otros gases como el argón (0,8%) y el ozono con una concentración de 0,0002%. Como se puede observar su presencia es muy reducida. Sin embargo su nivel aumenta a niveles perjudiciales para la vida cuando aparece el smog: mezcla de gases contaminantes procedentes de los motores de combustión interna ( nafta, gas, oil), refrigeración, calefacción y emanaciones industriales, entre los principales.
En la estratosfera (10 a 50 km) se encuentra una zona donde la concentración de ozono es mayor, con valores del orden de 0,0012 % en la ya mencionada capa de ozono.
A esta concentración y a esta altura el ozono se convierte en un protector de la vida en la superficie terrestre.
En la estratosfera la interacción entre la radiación ultravioleta procedente del sol, especialmente, y el gas atmosférico genera reacciones químicas que producen o destruyen compuestos. Uno de esos es el ozono.
La producción de ozono se origina en una molécula de O2.
La radiación solar rompe estas moléculas liberando dos átomos de O. La ruptura se produce a consecuencia de la energía que transporta la onda ultravioleta, la que excita y hace vibrar los átomos de la molécula hasta romper los enlaces químicos que las mantiene unidas.
Como el átomo de oxigeno es inestable reacciona con la primer molécula de O2 que encuentra para formar un nuevo enlace y así se genera la molécula triatómica de ozono O 3.
Las ondas ultravioletas que intervienen en la ruptura descripta son de una energía mayor ( mayor frecuencia) que las que intervienen en el proceso inverso, o sea, la transformación de una molécula de O3 en una molécula de O2 y un átomo de O.
El proceso normal es que en promedio haya un equilibrio entre la ruptura de moléculas de O3 ( u O 2) para producir átomos de O y la formación de nuevas moléculas de O3.
Manteniendo en un valor constante la concentración de O3 las ondas ultravioletas son filtradas en la estratosfera, pues tanto en la formación como en la destrucción de moléculas de ozono estas ondas pierden energía.
El espesor de la capa de ozono comenzó a preocupar a principios de la década del 70.En esa época se descubre el efecto dañino sobre el O3 por parte de los compuestos clorofluorocarbonados. Este compuesto químico, sintetizado en los laboratorios industriales, se emplea como propulsor gaseoso para pulverizaciones (spray), refrigerantes y otras aplicaciones. Este gas es muy estable y prácticamente no reacciona con otros compuestos químicos.
Por su estabilidad estos gases, una vez liberados, ascienden después de un largo tiempo a la estratosfera. Cuando llegan, la radiación ultravioleta por vibración rompe la molécula y libera átomos de cloro. Este cloro reacciona con las moléculas de O3 y las convierte en una molécula de O2 y un átomo de O. El cloro sobrevive a esta reaccion y queda libre para continuar con su acción depredadora..
Por supuesto los capitanes de las industrias hicieron todos los esfuerzos y gastos necesarios para negar esta acción destructiva de los clorofluorocarbonos. No importa la humanidad, lo importante es el capital.
Actualmente hay un gran debate sobre las posibles causas de la disminución del espesor de la capa de O3. Una teoría atribuye las causas a comportamientos anómalos de la actividad solar, otras a cambios en la circulación de los vientos de altura en la Antártida, pero los más sospechosos siguen siendo los clorofluorocarbonos.
NOTICIA
Se informa a los lectores e interesados que el presente número de esta Revista y algunos anteriores están a su disposición en la página web de la Universidad Nacional de San Luis. http://bib0.unsl.edu.ar/bibls/publ-online.html
Para consultas, sugerencias, etc., puede hacerlo por correo electrónico:
Email: cmaga@unsl.edu.ar
Editor: El Profesor de Ciencias, Departamento de Física,
Univ. Nac. de San Luis. C.C. 136 – CP: 5700 – San Luis