
EL PROFESOR
DE
CIENCIAS
Número 10 JULIO/99
Facultad de Ciencias Físico Matemáticas y Naturales
Universidad Nacional de San Luis
OBJETIVOS
Esta publicación está destinada a Profesores de Nivel Medio en Matemáticas y Física.
El objetivo fundamental es establecer una comunicación directa de la Facultad de Ciencias Físico Matemáticas y Naturales (UNSL) con dichos Profesores, a efectos de desarrollar actividades que permitan mejorar la calidad de su enseñanza en estas ciencias y, por lo tanto, mejorar la calidad de sus egresados.
El contenido de esta publicación estará constituido por artículos metodológicos e instrumentales para la enseñanza teórica y práctica de temas del currículum de nivel medio, problemas y su metodología de resolución, desarrollo de temas de actualidad en relación a su aplicación al currículum, prácticos de laboratorio, preguntas y respuestas para transferencia de conocimientos, noticias de carácter educativo en el área, evaluación, cartas, comentarios y artículos enviados por los docentes-lectores, donde puedan aportar, solicitar o compartir sus logros, necesidades, dudas y, finalmente todo artículo cuyo contenido los profesores soliciten, sugieran o sea oportuno incluir.
Señor Profesor:
Para lograr el propósito de mantener la edición de esta publicación, se necesita de la respuesta y colaboración de los destinatarios. Esto significa que es muy necesario, y se lo agradecemos desde ya, nos haga llegar sus opiniones, solicite y aplique el material que le ofrecemos, envíe artículos para publicar y difunda esta pequeña revista.
Muchas Gracias
INDICE
Publicación subsidiada por la Facultad de Ciencias Físico Matemáticas y Naturales de la Universidad Nacional de San Luis
IDEA Y REALIZACION: Lic. Carlos Magallanes
HTML Y Publicación en Web: Prof. Germán Roque Aras
El tema movimiento armónico simple está incluido en la mayoría de los programas de física de nivel medio. Para su enseñanza los profesores analizan dos sistemas que son muy apropiados; el sistema masa-resorte y el péndulo en la superficie de la tierra. Estos sistemas son muy útiles pues son sencillos y permiten analizar sin muchas dificultades, una gran cantidad de constantes y variables físicas de movimientos oscilatorios y periódicos. Además son, desde un punto de vista cinemático, un ejemplo de sistema con aceleración variable, donde hacer una extensión para aplicar la segunda ley de Newton, vista en temas anteriores.
Sin embargo, la real necesidad de estudiar estos movimientos oscilatorios es que son una introducción a un gran tema de la física: Vibraciones y ondas.
A mi entender, si no se aplican los conocimientos del movimiento oscilatorio a vibraciones y ondas mecánicas no tiene mucho sentido ahondar en su enseñanza. Esto es porque vivimos en un océano de vibraciones y ondas mecánicas y electromagnéticas. Por lo tanto es inexcusable la inclusión de estos temas en un currículum de física. Analice por un momento, la relación de vibraciones y ondas con los temas: acústica, luz, electromagnetismo, radiación, estructura de la materia, etc. y entenderá la razón de esta afirmación.
En el análisis físico del movimiento de estos sistemas se descubre que las condiciones para que se produzcan oscilaciones es que debe existir una fuerza central, o sea una que apunta siempre hacia un mismo punto. Suele denominarse fuerza recuperadora y al punto mencionado: punto de equilibrio. Luego que se avanza en el planteo de la ecuación de movimiento se descubre que para obtener una solución lineal se debe imponer una condición a esta fuerza recuperadora: que sea proporcional al apartamiento respecto del punto de equilibrio.
En el caso del sistema masa – resorte la fuerza recuperadora se origina en la deformación del resorte y en el caso del péndulo en una componente de la fuerza peso de la masa suspendida del hilo.
En el caso del sistema masa-resorte, la fuerza recuperadora cumple esta condición siempre y cuando el estiramiento sea pequeño para que no se supere el límite elástico del resorte, y en el caso del péndulo siempre que la amplitud sea pequeña.
En ambos casos las ecuaciones que describen el movimiento están limitadas a la condición de que el apartamiento respecto del equilibrio sea pequeño.
En símbolos matemáticos todo esto significa:
|
Resorte
(Pequeña amplitud)
|
Pendiente
Aquí se hace la limitación a pequeña amplitud
|
En ambos ejemplos ![]() es una
magnitud física propia del sistema. No depende de cómo se inicia el movimiento
(condiciones iniciales). Esta magnitud tiene dimensiones de frecuencia (S-1)
y es llamada frecuencia natural del sistema.
es una
magnitud física propia del sistema. No depende de cómo se inicia el movimiento
(condiciones iniciales). Esta magnitud tiene dimensiones de frecuencia (S-1)
y es llamada frecuencia natural del sistema.
Una vez obtenida la ecuación del movimiento, (1)
corresponde resolver la ecuación diferencial que contiene a las funciones x(t)
y ![]()
![]() , respectivamente,
que describe el movimiento de cada sistema.
, respectivamente,
que describe el movimiento de cada sistema.
Como ya se sabe, estas funciones son:
![]()
![]()
y (2)
![]()
![]()
A, ![]() y
y ![]() son parámetros
que dependen de las condiciones iniciales (posición y velocidad para t=0)
y una vez determinada caracterizan a un movimiento en particular.
son parámetros
que dependen de las condiciones iniciales (posición y velocidad para t=0)
y una vez determinada caracterizan a un movimiento en particular.
Las ecuaciones (2) con el w0 determinado representan, para el sistema correspondiente, todos los posibles movimientos oscilatorios que puede realizar y con la condición de pequeña amplitud ya mencionada.
A causa de la dependencia de x(t) y ![]() de la función
seno (o coseno) se le suele llamar al movimiento oscilatorio armónico.
de la función
seno (o coseno) se le suele llamar al movimiento oscilatorio armónico.
Relacionado con w0 está el período T del movimiento. Se entiende por período el tiempo que tarda el sistema en efectuar una oscilación completa, es decir el tiempo que tarda en pasar por un punto dos veces consecutivas y en el mismo sentido.
Para el caso del sistema masa-resorte es fácil determinar que:
![]()
Y para el sistema péndulo-tierra
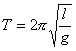
Obsérvese que en cada caso el período es constante y no depende de la amplitud. Solo depende de propiedades físicas propias e internas del sistema. En el primer caso, de una propiedad del resorte (su constante K) y de la masa del cuerpo sujeto a su extremo. En el segundo de la longitud l del hilo que forma el péndulo y de la aceleración gravitatoria en el lugar que se encuentra.
Resumiendo: la restricción a pequeña amplitud para las oscilaciones asegura que el periodo es constante y que solo depende de propiedades del sistema.
Se puede demostrar que cuando no se cumple la condición de pequeña amplitud, el período depende de esta. Los osciladores mencionados hasta aquí son ideales. No se ha mencionado la posibilidad de algún tipo de amortiguamiento. En la realidad todo oscilador está sometido a un amortiguamiento que hace que su energía inicial disminuya en el tiempo, hasta detenerse.
Cuando se incluye el amortiguamiento en el estudio del oscilador en los cursos básicos, se hacen simplificaciones para facilitar la interpretación de los resultados. Una simplificación es imponer la condición de baja velocidad a los componentes del oscilador. Esto permite introducir una dependencia lineal de la fuerza de amortiguamiento con la velocidad. Matemáticamente esto significa:
![]()
Fa (Fuerza de amortiguamiento)
Cuando V no es baja, Fa depende de potencias (de V) mayores que uno.
La otra condición es que el coeficiente b sea constante.
Bajo estas condiciones se obtiene la solución del oscilador débilmente amortiguado.
![]()
Siendo A0 la amplitud a t=0, ![]() =tiempo
de relajación, donde está incluida la constante de amortiguamiento, y w’ la
frecuencia de oscilación amortiguada que es levemente inferior a w0
y es función de ésta y de
=tiempo
de relajación, donde está incluida la constante de amortiguamiento, y w’ la
frecuencia de oscilación amortiguada que es levemente inferior a w0
y es función de ésta y de ![]() .
.
De todas maneras, w’ es constante, lo que significa que el período del oscilador débilmente amortiguado es constante y mayor que el correspondiente al caso ideal T0.
El desarrollo anterior puede generar en el alumno la idea de que todo movimiento periódico es independiente de la amplitud, haya o no amortiguamiento, si se cumple la condición de pequeña amplitud.
Hay varios ejemplos donde no se verifica esta situación. Aquí se mencionan solo el caso del trompo y de una pelota que rebota.
Cuando una pelota es dejada caer desde una altura h0 se observa que después de rebotar repetidas veces, cada vez alcanza menor altura. Cuando la pelota choca contra el piso su energía cinética se transforma en energía potencial elástica (o de deformación). Si el choque fuera perfectamente elástico, recuperaría toda la energía cinética y alcanzaría la altura inicial (supuesto que el rozamiento con el aire no efectúe trabajo sobre ella y la pelota pierda energía). En condiciones ideales la pelota oscilaría entre el punto de partida y el suelo.
Pero como sabemos, el choque no es elástico y cada altura es menor que la anterior. La energía mecánica de la pelota cada vez es menor.
Este movimiento "oscilatorio" no cumple la condición del armómico. ¿Por qué?. Porque la fuerza “recuperadora”, en este caso el peso de la pelota, es constante y no es proporcional al apartamiento del equilibrio, sea grande o pequeña la amplitud.
Esta observación nos da la pauta de que el período no tiene porqué ser independiente de la amplitud.
Verifiquemos esta afirmación en base a las conocidas ecuaciones de la cinemática.
La gráfica h(t) de la pelota tiene la forma
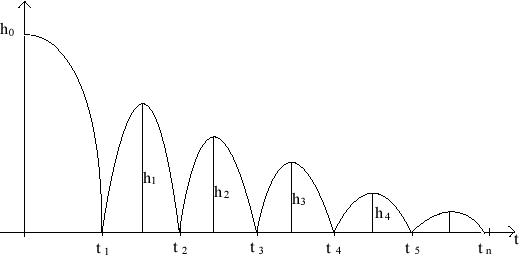
Si indicamos con Ti el tiempo que tarda la pelota en rebotar contra el suelo dos veces consecutivas. Entonces:
![]()
![]()
![]() (2)
(2)
El coeficiente de restitución, en base a su definición se puede expresar:
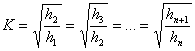 (supuesto constante)
(supuesto constante)
![]()
Reemplazando en (2)
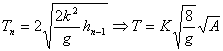
Indicando con A la amplitud del rebote anterior.
Se observa que el período depende de la raíz cuadrada de la amplitud y que aunque el choque fuera perfectamente elástico (K=1), la situación se mantiene.
Por lo tanto, como la amplitud de sucesivos rebotes va disminuyendo, causa de la pérdida de energía mecánica de la pelota, el período es cada vez más corto y la frecuencia de los rebotes aumenta.
El otro ejemplo donde es posible observar una dependencia del movimiento periódico con la amplitud es el trompo. Cuando un trompo gira, el momento de la fuerza peso genera la precesión. Esta precesión se observa por el movimiento circular del eje de rotación alrededor de la vertical que pasa por el punto de apoyo del trompo.
La velocidad angular de precesión Wp es inversamente proporcional
al momento angular![]() . Si el
sistema es cerrado
. Si el
sistema es cerrado ![]() se conserva
y por lo tanto Wp. Cuando hay pérdida de energía W disminuye y por lo tanto
también
se conserva
y por lo tanto Wp. Cuando hay pérdida de energía W disminuye y por lo tanto
también ![]() . En consecuencia
Wp aumenta. Esto hace que el período de rotación alrededor del eje vertical
disminuya.
. En consecuencia
Wp aumenta. Esto hace que el período de rotación alrededor del eje vertical
disminuya.
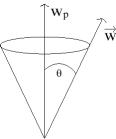
Lo que se observa es que la frecuencia de rotación del eje del trompo
alrededor de la vertical aumenta a medida que el ángulo ![]() que forma
con la vertical crece (ver figura).
que forma
con la vertical crece (ver figura).
Un ejemplo similar al del trompo, es el de una moneda apoyada en su canto y que gira alrededor de un eje vertical que pasa por su centro. A medida que pierde energía por el rozamiento empieza a inclinarse hasta que finalmente se detiene ...
El ruido que se escucha cuando hacemos la experiencia es el golpe del borde de la moneda contra la mesa. El punto de contacto de la moneda y la mesa recorre la circunferencia que define su borde. Si llamamos T al tiempo que tarda el punto de contacto en completar un giro, se puede demostrar que:
![]()
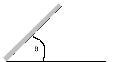
Siendo ![]() el ángulo
que forma el plano de la moneda con la mesa. A medida que
el ángulo
que forma el plano de la moneda con la mesa. A medida que ![]() disminuye,
cuadráticamente se reduce T y por lo tanto en esa misma proporción aumenta la
frecuencia. La observación de este aumento de frecuencia es mejor hacerla con
una tapa de cacerola en lugar de una moneda.
disminuye,
cuadráticamente se reduce T y por lo tanto en esa misma proporción aumenta la
frecuencia. La observación de este aumento de frecuencia es mejor hacerla con
una tapa de cacerola en lugar de una moneda.
- Profesor: Dígame alumno una forma de comprobar el efecto Doppler, usando la luz en lugar del sonido.
- Alumno: Hum ..., cuando es de noche, las luces de los coches se ven blancas cuando se acercan y rojas cuando se alejan.
¿Qué es un niño complejo?
Uno con la madre real y el padre imaginario
Alineación Planetaria Año 2000
Lic. L. Odicino
Entre los meses de marzo y junio del año 2000 se producirá una configuración muy especial de los planetas que son visibles a simple vista, estos son: Mercurio, Venus, Marte, Júpiter y Saturno que junto con nuestra Luna formarán un espectáculo que se repite aproximadamente cada 200 años.
Prevemos que con el advenimiento del milenio y esta especial configuración planetaria, los medios de comunicación producirán un cúmulo de información, alguna de ella buena y otra no tanto y que por ello, un profesor debe estar preparado para contestar y poner en el correcto contexto las preguntas y las inquietudes que esto puede provocar en sus alumnos, además de aprovechar la oportunidad para enseñar algunos conceptos de astronomía observacional.
Como sabemos, los planetas de nuestro sistema solar se mueven alrededor del sol a lo largo de órbitas elípticas. Para el caso de nuestro planeta, el plano que contiene al sol y a la tierra, junto con su órbita se denomina: plano de la eclíptica. Los planos que contienen las órbitas de los otros planetas forman ángulos pequeños respecto de nuestra eclíptica.
Por eso, desde la tierra se observa que los planetas están ubicados en una franja estrecha de la bóveda celeste.
Este hecho hace que el término “alineación” produzca alguna confusión, pues nunca pueden estar en la misma línea como lo indica tal palabra. Por ello en este texto emplearemos el término configuración. Luego esto nos llevará a expresar que lo que veremos es una particular configuración donde los planetas que mencionamos se ubicarán muy próximos entre sí en una región angular reducida de la bóveda celeste.
En la tabla que reproducimos a continuación se muestra un resumen de la configuración y fechas en las cuales estas ocurrirán.
|
PLANETAS |
FECHA |
SEPARACIÓN EN º |
|
Venus – Mercurio Marte – Júpiter Marte – Saturno Mercurio – Venus Mercurio – Júpiter Venus – Júpiter Mercurio – Marte Júpiter – Saturno Venus - Marte |
15 de Marzo 6 de Abril 15 de Abril 28 de Abril 8 de Mayo 17 de Mayo 19 de Mayo 27 de Mayo 21 de Junio |
2,1 º 1,0 º 2,2 º 0,3 º 0,8 º 0,01 º 1,1 º 1,1 º 0,2 º |
Como se puede observar de la tabla las cosas ocurrirán en un lapso de tiempo bastante grande y la mínima aproximación entre los 5 planetas más el Sol y la Luna ocurrirá el 5 de Mayo y todos estos astros se ubicarán en un círculo que tendrá aproximadamente 25º de diámetro y que por supuesto no será visible durante el día, por la luz solar, sólo será visible al atardecer.
A los fines de tener una idea de la separación que estos ángulos representan, en forma aproximada podemos decir que estirando nuestro brazo y cerrando el puño este cubre un círculo de 10º de diámetro, con la misma ubicación del brazo el ancho del dedo pulgar representa aproximadamente 1º y la separación existente entre la punta del pulgar y la punta del dedo índice con la mano abierta (lo que llamamos geme) representa un ángulo aproximado de 20º. Como sugerencia se puede verificar en clase estos datos, simplemente tomando el ancho del dedo por ejemplo con una regla y el largo del brazo con un metro y realizando el cociente entre este ancho y el largo tendremos el ángulo en radianes y cada alumno podrá tener su medida. Se puede determinar un valor medio para el curso y tomar éste para futuras determinaciones.
Configuraciones de este tipo han ocurrido antes como ya hemos dicho. La última fue el 5 de febrero de 1962, la separación de los 5 planetas más la Luna (sin el Sol), fue de 15,8º, la próxima será el 17 de Mayo de 2000, con 19,5º y la siguiente será el 8 de Setiembre de 2040 con 8,3º. Por otra parte, la única configuración similar a la del próximo 5 de Mayo, o sea con el Sol, la Luna y los 5 planetas, se producirá el 20 de Marzo de 2675, fecha en la cual la separación será de 22,6º.
En algunos medios se está hablando de los posibles efectos que sobre la Tierra puede tener esta particular configuración. Primero, y como dijimos antes, estas configuraciones se han repetido en el tiempo y no tenemos nada que relacione algún fenómeno natural tales como huracanes, terremotos, erupciones volcánicas con estas particulares posiciones de planetas de nuestro sistema solar.
Todos los fenómenos catastróficos que se asocian con la configuración que se viene, tienen que ver con las fuerzas de atracción gravitatoria. Esta fuerza es ejercida por cada astro y sobre cada uno de los otros compañeros de viaje y lo que un planeta siente es la combinación vectorial de las fuerzas que todos los otros ejercen sobre este en particular. Luego para una alineación, la fuerza resultante sobre la tierra sería la combinación de todas estas fuerzas juntas que producirían: a) tal tirón gravitatorio que podría sacarla de su órbita, b) tal tirón gravitatorio que podría volcarla, es decir inclinar su eje de rotación hasta 90º respecto al plano de la elíptica, c) estas fuerzas podrían deformar la tierra y esto producir terremotos, maremotos, d) la deformación podría romper la corteza terrestre y esto producir erupciones volcánicas y e) los menos agoreros predicen que las mareas serían particularmente altas produciendo inundaciones costeras.
Como vemos ya existen todo tipo de predicciones y tal vez algunas mas de las cuales no tenemos conocimientos o bien nuestra imaginación es escasa. Será interesante leer los horóscopos de los niños que nazcan en esos días.
Tratemos de cuantificar estas fuerzas para determinar si existe algo de verdad en los argumentos que se esgrimen para producir tales pronósticos catastróficos.
La fuerza de gravedad depende de dos cosas, la masa de los cuerpos y de la distancia que los separa. Un cuerpo de masa más grande, digamos el doble, ejerce el doble de fuerza, pero depende de la inversa del cuadrado de la distancia, un cuerpo que está al doble de distancia ejerce una fuerza 2 x 2 = 4 veces menor, un cuerpo que esta 10 veces más lejos ejerce una fuerza 10 x 10 = 100 veces menor.
Las mareas se originan en una variación de las fuerzas gravitatorias. Fácilmente podemos demostrar esto.
La fuerza gravitatoria que se ejercen un cuerpo de masa M y otro de masa m separados por uns distancia r, es:
![]()
Si al cuerpo de masa m lo movemos de r hasta r+Dr, el cambio en la fuerza es:
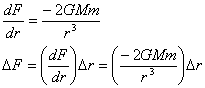
El cambio en la aceleración es entonces:
![]()
Como podemos ver las fuerzas de mareas dependen de la inversa del cubo de la distancia.
En la tabla que sigue se muestran y se comparan las fuerzas gravitatorias y las fuerzas de las mareas que ejercen sobre la Tierra los distintos planetas.
Tomamos como valor uno el de la Luna y excluimos la del Sol, pues si bien ejerce fuerzas gravitatorias importantes, es quien tiene el sistema solar ligado. La responsable de las fuerzas que ocasionan las mareas es la Luna debido a su proximidad. El Sol contribuye a las mareas pero en menor medida.
|
Planeta |
Masa x 1022 Kg. |
Distancia a la Tierra x 106 Km |
Gravedad Luna = 1 |
Marea Luna = 1 |
|
Mercurio |
33 |
92 |
0,00008 |
0,0000003 |
|
Venus |
490 |
42 |
0,006 |
0,00005 |
|
Marte |
64 |
80 |
0,0002 |
0,000001 |
|
Júpiter |
200.000 |
630 |
0,01 |
0,000006 |
|
Saturno |
57.000 |
1280 |
0,0007 |
0.0000002 |
|
Urano |
8.700 |
2720 |
0,00002 |
0,000000003 |
|
Neptuno |
10.000 |
4354 |
0,00001 |
0,000000001 |
|
Plutón |
~1 |
5764 |
0,000000006 |
0,0000000000004 |
|
Luna |
7.4 |
0.384 |
1 |
1.0 |
Hemos usado esta notación para resaltar el hecho de la pequeñez del efecto que producen, sobre las mareas, los otros planetas, respecto al que produce la Luna. Así por ejemplo Júpiter produce una fuerza gravitatoria del 1% de la que ejerce la Luna y las fuerzas de marea son de 6 partes por millón. Porcentualmente es 0,0006%.
Luego, si consideramos el hipotético caso de alinear los planetas de manera que la suma vectorial coincida con una suma algebraica para los vectores fuerzas gravitatorios no alcanzaría el 2 % (1,7%) de lo que ejerce la Luna, siendo el efecto de marea mucho menor.
No obstante, ¿este casi 2% será suficiente para producir algún efecto sobre la Tierra?. Pensemos que la Luna tiene una órbita levemente elíptica, en su punto mas cercano está a una distancia de 363.000 km y en su punto más lejano a 405.000 km, luego el efecto gravitatorio sobre la Tierra por la Luna fluctúa casi un ¡25%! en cada órbita. Es evidente que una variación del 2% no puede generar efectos de importancia.
Podemos prepararnos para disfrutar un espectáculo inusual que nos brindará la naturaleza donde la configuración de los planetas será verdaderamente curiosa. Pero debe ser observado en su correcto contexto.
Quienes deseen profundizar en este tema o tener más información, se pueden dirigir a las direcciones de Internet http://www.nasa.gov que es la página principal de la NASA y allí buscar sobre “alineación” o bien navegar en las direcciones relacionadas.
Aportes para la enseñanza de la Geometría
Poliominós
Todo empezó con un juego: el Tetris. ¿Cuántas formas diferentes se pueden hacer con cuatro cuadrados iguales unidos por un lado?
Empezamos a investigar y encontramos cinco formas distintas.
Los españoles les llaman Cuatrominós o Tetris. El nombre es totalmente lógico si pensamos que un dominó es la figura formada por dos cuadrados iguales. Sólo hay un Dominó y dos Trominó. ¿Y con cinco cuadrados iguales, o sea Pentominós o Pentis? Ahora encontramos doce, ¡Cómo se aumentaron! ¿Y con seis cuadrados iguales o sea Hexominós?, Aquí encontramos 35.
Hace más de 30 años, el matemático norteamericano Salomón Golomb acuño el término Poliominó para describir a cualquier figura plana formada uniendo cuadrados de igual tamaño por los lados.
Al llegar aquí nos preguntamos ¿Y estas figuras producen cubrimiento del plano? ¿O cubrimientos de otras figuras?
Nos pusimos a investigar y descubrimos que unas sí y otras no.
El campo para investigar no tiene límites.
En el convencimiento que la geometría es la gran ausente de la escuela argentina, y que un aprendizaje significativo se logra partiendo de lo concreto o manipulable hacia lo abstracto es que quiero hacer un aporte para su enseñanza contándole una experiencia didáctica con alumnos del secundario de 9º año y º1 año del polimodal ( 14 y1 5 años) del Instituto San Agustín, de San Luis, Argentina.
Ellos se plantearon los siguientes objetivos e hipótesis:
· Aprender a investigar
· Jugar.
· Participar de la Feria de Ciencias.
· Construir un grupo trabajando.
· Enseñarle a la comunidad que se puede aprender a través del juego.
· El Tetris produce cubrimiento.
· Los Poliominós producen cubrimiento.
· Al caer un Tetris y completar una o más líneas aparecen Dominós, Tetraminós y Cuadrados
Jugando al Tetris nos preguntamos ¿Cuántas formas diferentes se pueden hacer con cuatro cuadrados iguales unidos por un lado?
Hablamos con Rosita en el Club y ella nos dijo: “Me parece muy linda la idea, se puede presentar a la Feria de Ciencias”.
Empezamos a investigar.
Los españoles los llaman Cuatrominós a los Tetris.
El nombre es totalmente lógico si pensamos que un Dominó es la figura formada por dos cuadrados iguales.
![]() Sólo hay un Dominó:
Sólo hay un Dominó:
Ahora nos preguntamos ¿Y uniendo tres cuadrados?
Hay dos Trominós:
¿Y con cuatro? O sea
Cuatrominós o Tetris
Hay cinco Tetris o Cuatrominós
Las fichas Pentis o Pentaminós se logran uniendo cinco cuadrados iguales por sus lados.
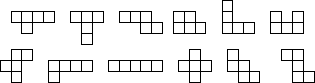 |
Hay doce Pentis o Pentominós. ¡Cómo se aumentaron!
¿Y con seis cuadrados? O sea Hexaminós
 |

Hay 35 Hexaminós.
Estamos muy sorprendidos de cómo aumenta la cantidad al aumentar un cuadrado. Hace más de Treinta años, el matemático Salomón Golomb, entonces un estudiante de la Universidad de Harvard acuñó el término “Poliominó” para describir a cualquier figura plana formada uniendo cuadrados de igual tamaño por sus lados.
Poliominó será el término genérico. Diez años después, Golomb describió su creación y aplicaciones en un libro, que no pudimos conseguir. En el mismo se hacía referencia a la posibilidad de utilizar triángulos de manera similar.
Aquí nos empezamos a preguntar sobre si estas figuras producen cubrimientos.
Nosotros al jugar con el Tetris, vemos que se van filas, si uno es hábil se van más filas.
Los cinco Tetris cubren una superficie de veinte casillas. Hasta ahora no pudimos cubrir un rectángulo de cuatro casillas por cinco casillas.
 |
Juntamos los cinco Tetris con un Pentis, o sea, completamos veinticinco casillas, un cuadrado con cinco casillas de lado, entonces pudimos lograr algunos cubrimientos.
 |
¿Cualquiera de los doce Pentis sirve para completar el cuadrado al unirse con los cinco Tetris? –Dice Mariano.
Hernán dice que no y Mauricio que si.
Sólo pudimos con ocho Pentis (o sea con los otros cuatro no pudimos)
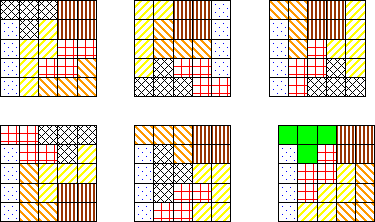 |
|||
 |
|||
Finalmente encontramos otra, pero con el mismo Pentis, solamente movimos de lugar los Tetris.
 |
Seguramente los creadores del juego Tetris conocieron muchas de estas propiedades.
¿Se podrán crear juegos con otros Poliominós?
El campo para investigar no tiene límites.
1. Hay un Dominó.
2. Hay dos Trominós.
3. Hay cinco Tetris o Cuatrominós.
4. Hay doce Pentis o Pentaminós.
5. Hay 35 Hexaminós.
6. Algunos Poliominós producen cubrimientos.
7. Con cinco Tetris no se cubre un rectángulo de 4 x 5 casillas.
8. Con cinco Tetris y un Pentis (sólo ocho de los doce) se cubre un cuadrado de 5 x 5 casillas.
1. Revistas acertijo.
2. Matemática 7º E. G. B. 3 _ Gustavo Barallobres. Editorial Aique _ 1997
3. Matemática 8º E. G. B. 3 _ Mirta Hanfling. Editorial Aique _ 1998
¿Qué sucede cuando n tiende a infinito?
Que infinito se seca
Estadística
En Nueva York un hombre es atropellado cada 10 minutos.
El pobre debe estar hecho polvo.
Problema unidimensional uniformemente variado
Lic. L. Odicino
Los movimientos uniformemente variados ocupan un punto importante
en todo programa de física elemental. La forma usual de tratarlos conduce al
conocimiento de la posición del móvil o bien su velocidad, a través de ecuaciones
que se deducen y se aplican, podemos decir que casi inconscientemente, como
una receta (expresión esta muy usada). Por ejemplo tal es el caso de las ecuaciones
![]() o bien
o bien
![]() .
.
El alumno que no se ha preocupado demasiado en sus deducciones, las aplica y difícilmente pueda generar sus propias ideas al respecto.
La presentación en forma de cocientes incrementales, y que conducen al concepto de derivada, representa una forma más rica y en algunos casos más simple de tratar problemas que aparentemente son tan complejos, lo que conduce a ni siquiera presentarlos en un curso de física elemental, cuando en realidad son de utilidad y de gran interés para alumnos de nivel medio.
Para dar un ejemplo de lo anterior plantearemos el caso de un movimiento con aceleración variable y que es de gran simplicidad. Para ello comenzaremos por el principio.
En la forma usual se fija la posición de un punto en un sistema unidimensional. Esto es, sobre una recta se fija un origen y un sentido. La posición queda determinada por la distancia de ese punto al origen. Es usual (y conveniente) que la posición se defina con un vector, para ello se define a éste por intermedio de un vector unitario que indica el sentido y cuantas veces está contenido en aquel.
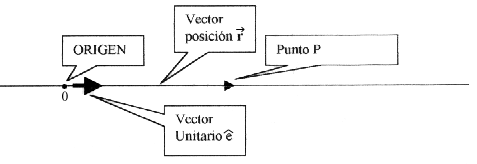
Luego el vector posición ![]() puede ser
puesto como
puede ser
puesto como ![]() . A continuación
podemos definir los vectores velocidad
. A continuación
podemos definir los vectores velocidad ![]() y los vectores
aceleración
y los vectores
aceleración ![]() . Lo que
hemos realizado son los pasos usuales de cualquier libro de física.
. Lo que
hemos realizado son los pasos usuales de cualquier libro de física.
![]()
Como ![]() es constante
por definición e igual a la unidad, la expresión anterior queda de la siguiente
manera.
es constante
por definición e igual a la unidad, la expresión anterior queda de la siguiente
manera.
![]()
Podemos escribir esto en forma mas compacta o bien en notación vectorial.
![]() con v =
ds/dt
con v =
ds/dt
También podemos definir una aceleración media ![]() (1)
(1)
Y una aceleración instantánea
![]() (2)
(2)
Por las mismas razones anteriores
![]() y también
podemos poner
y también
podemos poner ![]()
Veamos un ejemplo de aplicación de estos conceptos y que puede ser ilustrativo de un método de resolución. Además pone de manifiesto la existencia de las fuerzas de fricción sin haber definido a estas en forma formal.
Tomemos por ejemplo el transbordador espacial Este avión cohete, cuando termina su misión, debe aterrizar y lo hace con sus tanques de combustible agotados, esto implica que tiene una sola chance para aterrizar (no puede dar un giro extra sobre el aeropuerto) pero además, habiendo tocado tierra no dispone de combustible para frenar y lo hace exclusivamente con los frenos y un pequeño paracaídas que despliega en el momento del aterrizaje desde la parte de atrás del aparato. Esto constituye una aceleración de frenado producido por la fuerza de arrastre y que depende de la velocidad del aparato. Indiquemos la aceleración que produce este pequeño paracaídas con a y su valor dado por a = ‑0,004v2. Este avión cuando toca tierra tiene una velocidad de 100 m/s (360 km/h). Podemos preguntarnos el tiempo que tarda en llegar a los 10 m/s o bien en frenar totalmente con este sistema o bien la distancia que recorre para llegar a un determinado valor de velocidad.
De la expresión (2) y del dato inicial, se deduce:
a = A = dv/dt dv/dt = -0,004v2
Llegado a este punto podemos obtener las respuestas a la propuesta anterior (por un proceso iterativo) el cual puede ser ilustrativo de la forma de trabajo de un ordenador o bien de la introducción a técnicas de resolución numéricas.
También se puede resolver en forma analítica. Veremos a continuación la resolución por dos de estos métodos.
Partimos de la definición básica de aceleración media, esto es:
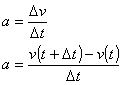
Para nuestro caso
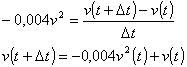 (3)
(3)
La ecuación (3), para aplicar un método iterativo la expresamos así:
![]() , donde
hemos supuesto que el incremento en el tiempo es uno. Luego si conocemos el
valor de la velocidad al tiempo i, lo calculamos para el tiempo i+1. Si, como
dice el problema al tiempo inicial (t0) la velocidad del avión es
100 m/s, al tiempo t1 es decir 1 segundo mas tarde, la velocidad
del avión será
, donde
hemos supuesto que el incremento en el tiempo es uno. Luego si conocemos el
valor de la velocidad al tiempo i, lo calculamos para el tiempo i+1. Si, como
dice el problema al tiempo inicial (t0) la velocidad del avión es
100 m/s, al tiempo t1 es decir 1 segundo mas tarde, la velocidad
del avión será
v(t1) = -0,004v2(t0) + v(t0) = -0,004(100)2 + 100 = 60 m/s
para el siguiente segundo, es decir al tiempo 2 seg. posterior al aterrizaje
v(t2) = -0,004v2(t1) + v(t1) = -0,004(60)2 + 60 = 45,6 m/s
para el tercer segundo el resultado es 37,28 m/s, para el cuarto segundo 31,72 m/s y así siguiendo.
Una gráfica de estos resultados vs. el tiempo queda de la forma:
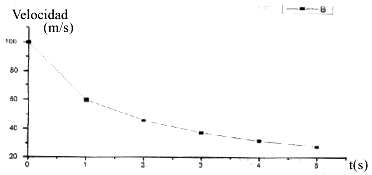
Fig. 1
Podemos hacer la siguiente observación: la curva tiene el aspecto de ser una exponencial decreciente y asintotica en el tiempo. Esto implica que el móvil nunca tendrá v=0, salvo en el infinito, y esto es debido a que no hemos considerado otros tipos de fuerzas, por ejemplo la fricción con el suelo o con el aire.
Una expresión de la forma
![]()
Se puede poner, por medio de separación de variables
![]()
La solución analítica de esta ecuación es
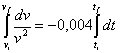
La solución de esta ecuación es
![]()
Como deseamos conocer la velocidad vf, un simple pasaje de términos permite poner esto como (suponiendo ti = 0 y vf = v)
![]()
Si graficamos esta ecuación
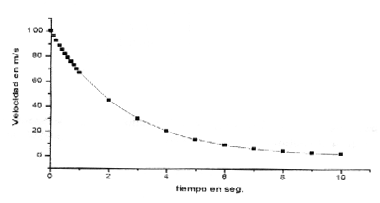
Fig. 2
Obtenemos una gráfica similar a la conseguida por el método numérico (fig. 1) donde podemos verificar que es asintótica en el tiempo.
Si repetimos el procedimiento con Dt menor, habrá que realizar mas cálculos para que la curva de fig. 1 se aproximara a la de fig. 2.
Este sencillo ejemplo es presentado aquí para mostrar lo que es un proceso iterativo y además para sugerir a aquellos profesores que tengan alumnos con prácticos de computación para efectuar la programación correspondiente y verificar este y otros resultados. Por ejemplo obtener para esta situación x(t).
El movimiento armónico simple debe estar presente en todo currículum de física, en razón de que es el punto de partida para estudiar las oscilaciones de cuerpos y, en general, sistemas de partículas.
El sistema físico sobre el cual se desarrolla el análisis dinámico y cinemático de las oscilaciones se denomina oscilador. Este concepto incluye tanto a sistemas simples por ejemplo una masa unida a un resorte, un péndulo, etc, como a sistemas mas complejos tales como una cuerda, el ala de un avión, un puente, etc.
Por supuesto que a nivel medio se utilizan los sistemas simples. Se estudia el oscilador en tres situaciones: oscilador libre de fuerzas exteriores, oscilador amortiguado y oscilador forzado.
Se restringe el movimiento del oscilador a oscilaciones pequeñas para que se cumpla la condición de proporcionalidad entre el esfuerzo y la deformación (Ley de Hooke). Esto también asegura que las ecuaciones de movimiento sean lineales, lo cual permite que sus soluciones sean obtenidas por sencillos procedimientos matemáticos.
Respecto a los movimientos del oscilador, el que aquí nos interesa es el movimiento oscilatorio forzado y de éste la resonancia.
Cuando se analiza un oscilador forzado se concluye que a la fuerza exterior periódica que actúa sobre él, este responde con oscilaciones de la misma frecuencia que ésta. La amplitud de estas oscilaciones forzadas depende de características físicas del sistema, del amortiguamiento, de la frecuencia de la fuerza exterior (w) y de la frecuencia natural del sistema (w0). Cuando la frecuencia exterior se aproxima al valor de la natural la amplitud del movimiento forzado del oscilador crece y llega a un máximo para un valor muy próximo a la natural w0.
Este fenómeno se denomina resonancia.
Cuando se estudia la resonancia, y por razones de simplicidad, se hace en base a un oscilador simple, por ejemplo sistema masa- resorte, pero debe recalcarse que, en general, todo sistema tiene la propiedad de resonar cuando es sometido a vibración forzada y a la frecuencia apropiada. Por ejemplo los instrumentos musicales a cuerda están constituidos por estas y por una caja, generalmente de madera. Estos sistemas, físicamente hablando, tienen un conjunto finito pero muy grande, de frecuencias a las cuales pueden resonar. La configuración de la masa de aire en el interior de la caja, de las placas que la conforman y de las cuerdas, en cada resonancia constituyen un MODO de oscilación. El modo de mayor amplitud es el de menor frecuencia a veces llamado modo principal o, para algunos autores, primer armónico.
Otro ejemplo de un sistema mas complicado lo podemos encontrar en un lavarropas cuando centrifuga. Si la distribución de la ropa y el agua no es simétrica el centro de masa de esta distribución se encuentra fuera del el eje de rotación del tambor. Esto genera un momento con componentes variables sobre los ejes principales del sistema y de frecuencia igual a la de rotación. Por lo tanto el sistema se comportara como un oscilador forzado y cuando la frecuencia de rotación sea próxima a la natural del sistema completo el sistema resonará y sus vibraciones se harán importantes. También podemos incluir entre sistemas con posibilidad de oscilaciones importantes a los edificios torres y de gran altura y a los puentes, en especial a los colgantes.
Aquí esta el objetivo de este articulo.
Cuando se pretende dar ejemplos de resonancia, frecuentemente se utiliza la ruptura del puente de Tacoma-Narrow en Estados Unidos en 1940.
Generalmente se aplica el ejemplo diciendo que el viento ejerció una fuerza variable sobre el puente con una frecuencia que coincidió con su frecuencia natural, entró en resonancia con amplitudes que su estructura no soportó y luego se derrumbó. Un alumno analítico, para entender el ejemplo y supuesto que estudió el tema con un sistema masa-resorte, hará una analogía entre ambos sistemas procurando encontrar equivalencia entre los distintos parámetros que actúan en ambas situaciones. Pero sin duda encontrara dificultades en entender el origen de "una fuerza periódica de frecuencia constante". Por ejemplo Resnick (1) cita: "El viento produjo una fuerza resultante cuyas fluctuaciones entraron en resonancia con la frecuencia natural de la estructura" Para adaptar esta explicación, deberíamos reescribir la definición de resonancia. Un intento puede ser:
"Siempre que un sistema físico puede oscilar (o vibrar) al ser accionado por una serie de pulsos periódicos de frecuencia igual a la natural del sistema, efectuará oscilaciones de gran amplitud "
Esta definición exige al viento que envíe sobre el puente golpes de aire y con una frecuencia casi constante y sostenida en el tiempo. No creo que esto pueda convencer a un alumno que piensa.
Algunos autores han procurado encontrar la fuente de la periodicidad necesaria de la fuerza excitadora en la formación de vórtices.
Esto significa: cuando una masa líquida o gaseosa encuentra un obstáculo en su camino, las líneas de corriente se separan y vuelven a unirse después de pasarlo. Esto sucede bajo condiciones muy especiales que dependen de la forma del obstáculo y de la velocidad La forma de este está relacionada con lo que comúnmente se denomina aerodinámica. En el diseño de automóviles, lanchas, trenes y aviones la forma aerodinámica es de vital importancia para disminuir la resistencia al avance y la reducción de turbulencias.
Cuando el móvil no tiene forma aerodinámica, después que el fluido lo pasa se forman cadenas de vórtices a partir de cierta velocidad. Las líneas de corriente se separan del cuerpo y no contornean sus bordes. Por vórtices se significa: concentración de partículas del fluido que se mueven en trayectorias circulares. Comúnmente se conocen como remolinos.
La frecuencia con que aparecen y desaparecen estos vórtices se traduce en compresiones y depresiones del aire que está después del puente. Esta frecuencia fue identificada por algunos autores como la del agente exterior periódico que generó las oscilaciones del puente hasta su ruptura. Este tipo de movimiento se conoce como vibración inducida por vórtices.
Sin embargo de acuerdo a Billah y Scanlan (2) los registros efectuados durante el colapso del puente, o sea la velocidad del viento (67 km/h) y la frecuencia de oscilación del puente en el momento del colapso fue de 0,2 Hz. Esta frecuencia no coincide con la que corresponde a esta velocidad deducida de la relación de Strouhal (1 Hz). (Referencia en Ref 2).
Brillah y Scanlan (2) explican que ensayos con un modelo a escala del puente Tacoma mostraron la existencia de un modo torsional no acotado de amplitud creciente con la velocidad del viento.
La repetición y ampliación de este experimento mostró definitivamente que la causa de la destrucción del puente fue un modo ondulatorio torsional generado por la compleja interacción de los flujos de aire que pasaban por encima y por debajo del puente.
Resumiendo, y a la vista de todo lo anterior se concluye que la directa analogía entre un oscilador simple en resonancia y la destrucción del Tacoma no es apropiada porque genera dudas y tal vez confusión en la mente de los alumnos.
1. HALLIDAY – RESNICK. Física. Parte I. CECSA.
2. BILLAH Y. SCANLAN, R. Resonance, Tacoma Narrow Bridge failure and undergraduate physics textbooks. American J. of Physics 59 (2). Febrero 1991.
Propagación de ondas electromagnéticas en un medio de índice de refracción variable
En la enseñanza de las leyes de la refracción se introduce el concepto de índice de refracción absoluto y relativo. Siempre se hace esta presentación para medios homogéneos e isotropos.
El paso siguiente es verificar las leyes mencionadas con incidencia de la luz en superficies planas. Se hacen también algunas aplicaciones a sistemas de una o mas placas transparentes y paralelas, prismas, etc.
El estudio de las lentes se introduce aplicando las leyes de la refracción a superficies curvas.
¿Qué sucede cuando el medio no tiene un índice de refracción igual en todos sus puntos?.
Analizaremos aquí un ejemplo para contestar a la cuestión planteada. El ejemplo se relaciona con la propagación de ondas de radio (ondas electromagnéticas) en la ionosfera.
Por la naturaleza de la ionosfera, el índice de refracción del gas que la constituye varía con la altura. O sea es una masa gaseosa de índice de refracción variable.
La ionosfera es una capa de la atmósfera terrestre que se encuentra a partir de los 80 km de altura hasta los 150 km, aproximadamente. Estos límites son aproximados, pues la atmósfera terrestre es un sistema dinámico de mucha actividad. Los efectos de esta actividad son conocidos por el hombre en sus aspectos positivos y negativos. La causa de la variación del índice de refracción en la ionosfera es su naturaleza plasmática. Esto significa que el gas que la constituye es un plasma.. En Física se entiende por plasma un gas altamente ionizado con baja densidad de partículas.(1). Otra definición de plasma (2) lo describe como un fluido conductor con varios componentes constituidos por electrones y distintos iones moleculares. La ionización presente en la ionosfera es producida por la radiación solar.
Los electrones e iones presentes en el plasma ionosférico interactúan con los campos eléctricos y magnéticos. En particular con los campos de las ondas electromagnéticas. La capacidad del plasma para efectuar oscilaciones y bajo ciertas condiciones, permite la propagación de estas ondas. El estudio de los posibles movimientos de un plasma por la acción de campos eléctricos y magnéticos conduce a ecuaciones no lineales, bastante complejas, que describen sus oscilaciones.
Hay dos tipos de oscilaciones electrostáticas del plasma: de alta frecuencia (oscilaciones electrónicas) las que por su rapidez no pueden ser seguidas por los iones pesados y las oscilaciones lentas las que pueden ser seguidas por dichos iones. Nos interesan las primeras.
Cuando el campo de la onda actúa sobre el electrón este se desplaza una distancia x y sobre el actúa una Fuerza = -e.E, siendo E el campo local.
Se puede demostrar que este campo E es proporcional al desplazamiento del electrón, por lo tanto estamos en la situación de una partícula sometida a una fuerza recuperadora proporcional al desplazamiento. Es de esperarse entonces que la fuerza eléctrica que actúa sobre el electrón sea periódica y que este realice oscilaciones. También debe existir una frecuencia natural propia del sistema de electrones como en todo oscilador. Esta frecuencia natural debe depender exclusivamente de características físicas del sistema.
Esta frecuencia existe y se llama frecuencia del plasma.
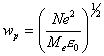 (1)
(1)
Siendo N la densidad electrónica, e la carga del electrón y Me
su masa, ![]() es una
constante (la permitividad del vacío).
es una
constante (la permitividad del vacío).
En los cursos de nivel medio el índice de refracción se presenta como una cantidad real. Pero cuando el medio es conductor, la conductividad y el índice de refracción pueden ser reales, imaginarios puros o complejos.
En un plasma, además de la frecuencia wp, también interesa la frecuencia de colisión fc.
Cuando fc << wp el plasma se denomina débilmente amortiguado. Cuando la frecuencia de la onda es alta (w > wp) el índice de refracción es real. El plasma actúa como un medio transparente.
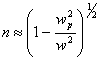 (2)
(2)
Cuando fc < w < wp la onda es atenuada exponencial mente (exponente negativo).
Cuando w < fc el índice de refracción es complejo. El plasma se comporta como un conductor y su conductividad es real.
Vemos, finalmente, que para que una onda electromagnética se propague en el plasma ionosférico su frecuencia debe ser mayor que la frecuencia del plasma wp. Para frecuencias menores a ésta, no habrá propagación
Si en la expresión (2) reemplazamos wp por su valor dado por (1):
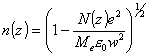 (3)
(3)
Obsérvese que cuando hay propagación (w > wp), n < 1. A medida que ascendemos en la ionosfera la radiación solar genera mas ionización, aumentando wp y, en consecuencia, disminuyendo n. Esta dependencia de n con la altura z ha sido indicada en la expresión (3).
Para analizar la influencia de la dependencia de n con z analizemos que le sucede a una onda electromagnética emitida por una antena sobre la superficie terrestre y que se propaga hacia la ionosfera.
Supongamos que la onda atraviesa un límite imaginario entre dos capas de la ionosfera cuyos respectivos índices sean n1 y n2. La onda va ascendiendo desde el medio 1 (n1) hacia el medio 2 (n2). Por lo anterior n1> n2.
Por la ley de Snell:
![]()
![]() : ángulo
de incidencia,
: ángulo
de incidencia, ![]() : ángulo
de refracción
: ángulo
de refracción
Operando: ![]()
Por ser n1> n2 debe ser ![]() >
> ![]() o sea el
rayo refractado se aleja de la normal, que en este caso es la vertical z.
o sea el
rayo refractado se aleja de la normal, que en este caso es la vertical z.
Si este proceso continua, es decir sigue disminuyendo el índice de
refracción a medida que la onda se propaga, la dirección del vector propagación
![]() ira rotando
hacia la horizontal. Superado el punto donde
ira rotando
hacia la horizontal. Superado el punto donde ![]() es horizontal,
el proceso se invierte, o sea la onda se propaga hacia regiones de índice creciente
y por lo tanto el rayo refractado se acerca a la vertical z..
es horizontal,
el proceso se invierte, o sea la onda se propaga hacia regiones de índice creciente
y por lo tanto el rayo refractado se acerca a la vertical z..
Como resultado final de este proceso de variación continua de la dirección de propagación de la onda, la trayectoria del frente de onda será una curva parabólica en el plano vertical y la onda retornara a tierra.
Resumiendo: la onda electromagnética que parte de un punto de la superficie terrestre, indirectamente y mediante sucesivas refracciones en las capas de la ionosfera retornara a tal superficie a una distancia que puede ser de muchos kms, medidos desde la antena emisora.
La intensidad de radiación de una dada región de la ionosfera varía ampliamente durante el día. Mientras el sol está sobre el horizonte, la ionización es mayor que durante la noche.
Se define la densidad electrónica crítica Nc
![]()
Esta densidad marca el límite para el cual el plasma ionosférico es transparente a las ondas electromagnéticas.
Cuando la onda llega a esta capa es totalmente reflejada. La altura a la que se encuentra esta capa varía durante el día, es menor cuando hay luz solar y aumenta durante la noche. Por lo tanto el alcance de una emisora de ondas de radio será mayor durante la noche y menor durante el día.
1. WANGSNESS, R. Electromagnetic Field. J Wiley and sons.
2. JACKSON, J. D. Classical Electrodynamics.
3. REITZ – MILFORD – CHRISTY. Fundamentos de la teoría electromagnética. Addison-Wesley Iberoamericana.
Una copa dejada caer desde poca altura se rompe si golpea contra un piso de baldosas. Sin embargo se puede lograr que esa copa cayendo desde la misma altura al caer sobre una superficie blanda, por ejemplo una alfombra, una cama, etc. no se rompa. ¿Cómo se explica, en términos físicos esta diferencia?
Es un envase moderno, liviano, irrompible, casi totalmente biodegradable. Por su forma ahorra espacio en el almacenamiento.
Fue creado por Ruben Rausing en Suecia hacia 1951. Hoy se usa en el envasado de líquidos, yogurt, leche, vino, etc. Es un envase liviano, lo cual es fundamental para el almacenamiento y transporte de líquidos en cantidades importantes.
Las paredes de un envase tetra brik están constituidas por capas de cartón y polietileno para productos pasteurizados y además una lámina de aluminio para productos de larga duración.
La capa de cartón cumple la función de dar rigidez y forma al envase, las de polietileno son barreras contra la humedad, bacterias y para lograr estanqueidad del envase. La capa de aluminio es una barrera contra la luz, los olores, oxígeno, etc.
El origen del nombre es porque inicialmente tenían forma de un ladrillo (brik en Inglés). Tetra por tetraedro.
“La educación comienza cuando se nace y termina cuando se muere”
En el número anterior (Nº 9) dejamos planteados algunos problemas para entretener a nuestros lectores. Aquí van nuestras respuestas.
Una bola de acero cae verticalmente desde una cierta altura. Cuando llega al suelo rebota. Si el suelo es duro, por ejemplo mármol, rebota a una altura mayor que si cae en una superficie blanda, por ejemplo asfalto. ¿Cómo explica esto?.
La colisión entre la esfera de acero y el mármol se aproxima a la elástica, en cambio contra el asfalto se aproxima a la inelástica. La pérdida de energía cinética del sistema en el primer caso es menor que en el segundo. Por lo tanto la velocidad inicial al iniciar el rebote en el primer caso es mayor que en el segundo. Esto hace que la altura alcanzada también sea mayor.
Un rifle está colgado mediante dos hilos, uno en cada extremo que lo mantienen horizontal y le permiten oscilar. Si el rifle es disparado, en que caso la bala llega más lejos, cuando:
a) Se lo inmoviliza de tal modo que no pueda retroceder, o
b) Cuando se lo deja libre para oscilar por el retroceso?
Después del disparo, cuando el rifle puede oscilar, absorbe parte de la energía liberada por la explosión, por lo tanto la bala recibe menos energía cinética al partir que en el caso de que no haya retroceso.
Entonces el alcance será mayor para el caso en que el rifle se mantiene fijo.
1) ¿Por qué es incómodo e ineficiente jugar con un futbol desinflado?
Mientras más inflado está el futbol, más se aproxima la colisión con el pié a ser elástica. Una misma patada impartirá más energía cinética mientras más se aproxima a ser elástica. Por eso, si el futbol está poco inflado, esta energía transmitida será menor y por lo tanto menor la eficiencia del puntapié.
2) ¿Por qué es necesario flexionar las piernas al saltar desde una cierta altura, por ejemplo desde una pared, una ventana, etc.?
¿Qué se siente si se llega al suelo con las piernas rígidas y sin flexionar?
Al caer, por reacción, los pies reciben la misma fuerza que el cuerpo ejerce sobre el piso. Si no se flexionan las piernas y se contraen los músculos para absorber el efecto de la fuerza, ésta actuará directamente en la columna vertebral, la cual tiene partes rígidas (vértebras) y flexibles (discos).
Un golpe fuerte puede fragmentar un disco y generar una hernia de disco.
Por otra parte, la fuerza se transmite parcialmente por la columna hasta la nuca y el cerebro.
Un resorte de constante K1 sostiene a otros dos de constante K2 y K3, respectivamente. Los resortes K2 y K3 están sosteniendo en paralelo a una masa m. ¿Cuál será el período de oscilación de este sistema?. Dar la solución en función de m y de las constantes K1, K2 y K3.
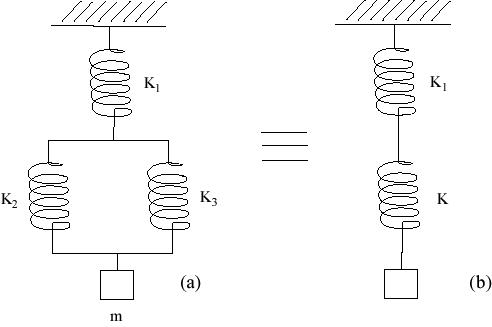
La combinación en paralelo de K2 y K3 se puede reemplazar por un resorte K de constante:
K = K2 + K3
La combinación en serie (parte b de la figura) entre K1 y K da una constante KT resultante que cumple:
![]()
entonces: 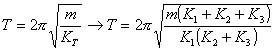
Las cerdas de un pincel fino permanecen separadas cuando está seco pero permanecen juntas cuando está mojado. ¿A qué se debe esto?
La tensión superficial tiende a minimizar la superficie de la película de líquido entre cerdas adyacentes del pincel.
NOTICIA
Se informa a los lectores e interesados que el presente número de esta Revista y algunos anteriores están a su disposición en la página web de la Universidad Nacional de San Luis. http://bib0.unsl.edu.ar/bibls/publ-online.html
Para consultas, sugerencias, etc., puede hacerlo por correo electrónico:
Email: cmaga@unsl.edu.ar
Editor: El Profesor de Ciencias, Departamento de Física,
Univ. Nac. de San Luis. C.C. 136 – CP: 5700 – San Luis