Proyecto Educativo de la Facultad de Ciencias Físico Matemáticas y Naturales
Universidad Nacional de San Luis
Nº1 - 2003
Equipo: Lic. Luis Odicino - Dr. Armando Catenaccio - Lic. Luis Santágata - Lic. Daniel Perelló
odicino@unsl.edu.ar
HTML y publicación en Web: Lic. Liliana E. Arce
Distribución gratuita
|
Indice Editorial En una noche despejada y sin luna Los grandes pensadores griegos Tiro de proyectil Una curva con alcurnia, la braquistocrona Encuesta |
|
EDITORIAL Hemos cumplido un etapa y empezamos otra que esperamos sea tan fecunda y plena de satisfacciones como la primera. Hemos ampliado nuestros colaboradores permanentes, hemos reorganizado la estructura de funcionamiento del PROFESOR DE CIENCIAS, hemos cambiado el director del proyecto educativo y le deseamos suerte al anterior responsable en sus nuevas tareas y responsabilidades. Deseamos agradecerle además, haber iniciado esta "patriada" que nos permite ahora estar con el amigo lector. nuevamente y renovados. Esta publicación, por ahora gratuita, y esperamos mantenerla así, forma parte de un proyecto educativo cuyo aporte económico y contralor se hace por medio de la Facultad de Ciencias Físico, Matemáticas y Naturales de la Universidad Nacional de San Luis. Nuestro propósito principal sigue siendo el tener un espacio donde los profesores de física y matemáticas puedan consultar, leer, y comunicar nuevas, ingeniosas y entretenidas formas de enseñar nuestras materias. El propósito sigue siendo el mismo, pero hemos ampliado nuestra visión a las ciencias naturales. Así el lector podrá encontrar en nuestras paginas temas de Biología, Geología, Informática, Química además de las tradicionales Física y Matemática. Hemos desarrollado un nuevo formato para nuestra revista donde aparecen secciones que estarán dedicadas a temas específicos, por ejemplo una sección donde se incluirá la actividad institucional de la UNSL relacionada con nuestros intereses, tales como conferencias, becas, cursos, etc. Esperamos que sea del agrado del amigo lector y nos hagan llegar sus criticas y sugerencias al respecto. Estamos gestionando nuestra pagina Web donde los usuarios de la red podrán consultar tanto la revista como temas relacionados.- En fin, tratamos de renovarnos para permitir una mayor comunicación con el amigo y colega docente que nos lee. Debido a los continuos recortes presupuestario es que debemos confirmar al lector interesado por lo que solicitamos nos haga llegar, ya sea por correo ordinario o bien por e -mail el formulario que se adjunto debidamente conformado.- Adherimos sin vacilaciones al sistema publico y gratuito de enseñanza que permitió a la Argentina ubicarse en un lugar de privilegio en el concierto de las naciones y que permite entre otras realidades estar con Uds. en esta nueva etapa del PROFESOR DE CIENCIAS. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Al Indice | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
LLUVIA DE ESTRELLAS  . En una noche despejada y sin Luna, ocasionalmente vemos el rastro de una estrella fugaz que surca el cielo. Estos son meteoros esporádicos. En ciertas épocas del año, estas estrellas fugaces parecen aumentar en número y salir de una región especifica del cielo, a esto le llamamos lluvia de estrellas. ¿Que son las lluvias de estrellas?.Lo que realmente vemos son partículas sólidas provenientes del espacio relacionadas siempre con los restos que dejan los cometas, más grandes que un átomo pero mucho más pequeñas que los asteroides y que se queman en la atmósfera terrestre. En el espacio, estos bólidos se le denomina meteoroides. Ellos entran en la atmósfera y se consumen antes de caer al suelo. Algunos logran sobrevivir al paso por la atmósfera terrestre y si cualquier parte de este meteoroide llega a la superficie de la Tierra, se le denomina meteorito. La lluvia de estrellas ocurre cuando la órbita de la Tierra cruza por los restos de partículas de la órbita de un cometa. Aquí se encuentra una concentración de partículas de tal forma que el numero de cuerpos entrando a la atmósfera es mayor y da la ilusión de una lluvia. A continuación la tabla de las lluvias de meteoros más importantes en el año. Las fechas son las correspondientes al año 2003. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| La mejor forma de observar una lluvia de estrellas es situándose en un lugar apartado de las luces de la ciudad, recostarse en el suelo, en una bolsa de dormir o en una silla reclinable, es la forma más cómoda de observar. No es necesario el uso de telescopios o binoculares, estos instrumentos limitan el campo de visión, permiten observar una estrecha porción de cielo y una estrella fugaz, en general, proviene de regiones amplias del espacio. Luego necesitamos solo nuestros ojos y un poco de paciencia, por lo menos observe durante media hora. Permita que sus ojos se adapten a la oscuridad. PROYECTOS DE OBSERVACIÓN. Trata de trazar el camino de los meteoros de cierta lluvia, todas las trayectorias parecen converger en un mismo punto en l cielo llamado el radiante. El efecto es perspectiva ya que los meteoros llegan en líneas paralelas a la atmósfera de la Tierra. De esta forma podemos determinar si la lluvia corresponde a la constelación de donde se sabe que proviene. Registrar el numero y duración de los meteoros es una tarea que podemos realizar. Necesitamos un reloj exacto y un bloc de notas para anotar las observaciones. Contar, calcular el tiempo que dure el meteoro en el cielo, la longitud de su estela, el color, su brillo. Es más conveniente tener la ayuda de una persona para que realice las anotaciones para no distraerse de la observación. Algunas prefieren grabar sus observaciones. Fotografía. Para fotografiar lluvias de estrellas necesitamos una cámara que permita exposición de tiempo indefinida, "B", un tripie y un lente con apertura de f/2 o f/1.4, película ISO 400,800. Colocaremos la cámara apuntando hacia cualquier parte del cielo, de preferencia hacia la constelación en donde tenga el radiante. Y tomaremos una exposición indefinida hasta que algún meteoro cruce por la región del cielo hacia donde hemos apuntado nuestra cámara. ALGUNAS EFEMÉRIDES PARA EL AÑO 2003, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Al Indice | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
En este caso nos ocuparemos de ARISTARCO DE SAMOS, nació alrededor del 310 AC y si bien la fecha de fallecimiento permanece incierta se cree que fue alrededor del 230 AC. Existió otro Aristarco, el de Samotracia, este último se dedicó a las letras, director de la biblioteca de Alejandría, compilo y corrigió los poemas Homéricos, mientras quien nos interesa el de Samos se dedico a la astronomía y fue acusado de atentar contra los dioses por afirmar que la tierra giraba alrededor del sol y alrededor de su propio eje. Su teoría, radical, que hacia retroceder las estrellas a una distancia infinita, tuvo una fría acogida entre los astrónomos y filósofos de su época, luego su teoría quedaron en el olvido. Le cupo el honor de ser el primer astrónomo que calculo a distancia tierra-luna, usando para ello la información que produce un eclipse total de sol. Veamos como hizo esto. Para ello nos ayudamos del esquema que se muestra 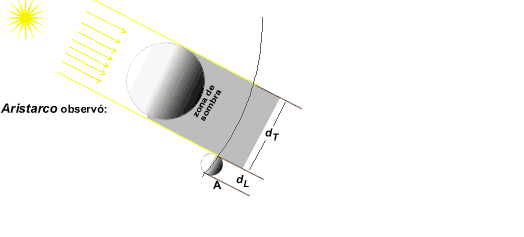 Posteriormente una medida del ángulo visual que sostiene la luna desde la tierra que midió y arrojo como resultado una cifra de aproximadamente 1/720 de la circunferencia que tiene un radio igual a la distancia tierra -luna, y que llamaremos TL Ahora una simple proporcionalidad le permitió a Aristarco conocer la distancia Tierra-luna en función del diámetro de la tierra. Para ello razonó que si el ángulo visual que la luna mantiene con un observador de la tierra es 1/720 de una circunferencia. Por lo tanto se debe cumplir que un giro completo de un observador en la tierra sea equivalente a 720 veces el diámetro de la luna, esto es: 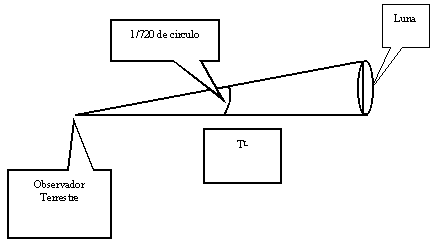 pero de la observación de los eclipses demostró que dT = 4 dL se tiene en definitiva que: Nada mal si tenemos en cuenta que el valor aceptado actualmente de la distancia tierra - luna en diámetros terrestres es de 30.17 Podemos ahora recordar que por la misma época, entre (276 - 194 AC) aproximadamente, también existió otro astrónomo famoso Eratóstenes de Cirene, quien fue capaz de medir la circunferencia de la tierra con la simple observación de la diferencia en la sombra de dos estacas ubicadas en ciudades distantes 800 Km. Sus cálculos le permitieron establecerla en 40000 Km. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Al Indice | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Un proyectil es disparado de un arma en forma horizontal hacia un blanco que se encuentra alineado con el cañón del arma, este blanco se encuentra a una distancia determinada del arma, el proyectil, como todos sabemos, realizará una trayectoria curva e impactará, a una distancia Dy del blanco. Si nuestro propósito es atinar al blanco debemos corregir esta distancia disparando levemente hacia arriba, ¿nuestro calculo de corrección debe ser igual a Dy, levemente mayor o levemente inferior a Dy?. 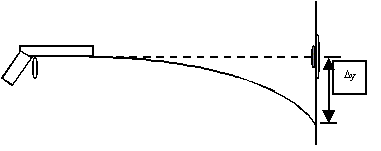 La respuesta correcta es que debe ser levemente mayor a Dy, ya que la corrección introduce un ángulo de disparo y por consiguiente existen componente de la velocidad inicial según el eje x y según el eje y.- Veamos si podemos cuantificar esta situación.- Primero encontremos el valor de Dy , suponiendo para ello que el blanco se encuentra a una distancia d, y la velocidad inicial de la bala es de v0. El tiempo que la bala tarda en llegar al blanco, despreciando la fricción es: Luego Dy es igual a: ya que no hay una componente de velocidad inicial según el eje y.- La situación con la corrección para dar en el blanco es diferente, supondremos que el ángulo de corrección es a, luego la situación se esquematiza en el dibujo siguiente: 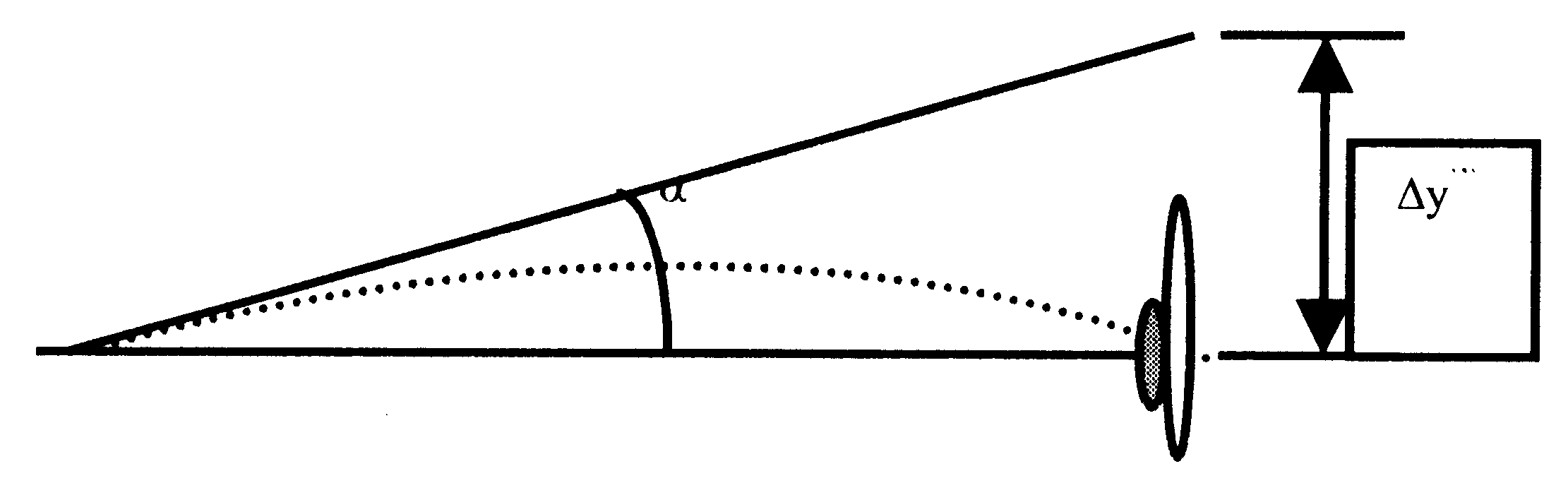 Llamaremos al la distancia de corrección Dy'.- Ahora el proyectil tiene dos componentes de velocidad inicial. V0x y V0y, cada una de ellas se pueden poner en función de la V0 y el ángulo como también podemos encontrar una expresión para Dy'. 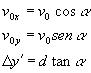 En este caso el tiempo que demora el proyectil en llegar al blanco lo denominaremos t' y debe ser igual a dos veces el tiempo que el proyectil demora en llegar a su máxima altura, ts, sobre la línea recta que une el blanco con el cañón del arma. Podemos escribir luego el siguiente grupo de ecuaciones: 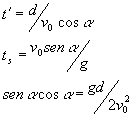 Operando algebraicamente, sin hacer operaciones difíciles pero tal vez algo laboriosas, llegamos a que: Expresión final de nuestra demostración, obsérvese que el denominador es siempre positivo y menor que 1, luego es Dy' siempre mayor que Dy, pero como este ángulo es muy chico la corrección es pequeña. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Al Indice | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Si preguntamos a cualquier persona que grafique la trayectoria que un cuerpo hace cuando se desplaza de un punto a otro de menor altura, en un campo gravitatorio, es probable que este diga que la trayectoria es una recta que una esos puntos. En contra de lo que parecería a primera vista, la línea recta no es la que permite el descenso más rápido, sino una curva que se llama braquistocrona (del griego braquis, corto, y cronos, tiempo), también conocida como cicloide. La braquistocrona fue encontrada a fines del Siglo 17 y su historia es muy interesante, ya que involucró a los más grandes matemáticos de esa época. Recordemos que en 1686 Isaac Newton publicó Los Principia, obra que se considera marca el nacimiento de la física teórica. Newton mostró como calcular a trayectoria de los planetas, encontró la expresión analítica para la ley de gravitación universal y para ello desarrollo una herramienta matemática, que él denominó fluxiones y que ahora constituye una de las mas poderosas herramientas en ciencias que es el cálculo diferencial e integral La obra de Newton contradecía, o bien no necesitaba de supuestos que otras teorías si lo hacían, tal el caso de los movimientos de éter, propuesto por Descartes, esto llevo a que no fuera aceptada de inmediato por sus colegas de las otras universidades, por otra parte, Newton y Leibniz se enfrascaron en un una discusión, bastante agria por cierto, sobre la paternidad del cálculo diferencial e integral que ambos descubrieron en forma simultánea e independiente. A pesar de todo, la física de Newton era tan convincente que se impuso poco a poco. Newton, quien era un profesor de Cambridge, se volvió una celebridad en su patria. Esto hizo que su amigo y protector Charles Montagu, futuro Barón de Halifax, le consiguiera el puesto de director de la Casa de Moneda, en Londres. El puesto de director no tenía mayores complicaciones, pero Newton no se lo tomó así, sino que se volvió un activo y responsable funcionario. A su cargo quedaron la reforma monetaria en el reino, la acuñación de nuevas monedas y la ejecución de los falsificadores en la horca. En junio de 1696, el gran matemático de origen holandés Johann Bernoulli decide arrojar un reto a "los más brillantes matemáticos del mundo", proponiendo el problema de la braquistocrona en la revista Acta Eruditorum. Siendo Bernoulli amigo de Leibniz, el desafío tenía aparentemente intención de desafiar a Newton, quien se había alejado de las actividades científicas. Y es que el problema requería del cálculo diferencial e integral, cuya paternidad se discutía. Según cuenta John Conduitt, amigo y biógrafo de Newton, el director de la Casa de la Moneda se enteró del desafío realizado, "en medio de la prisa por la gran acuñación, regresó muy cansado a su casa a las cuatro de la tarde, pero no se fue a dormir hasta haber resuelto el problema, lo cual le tomó hasta las cuatro de la mañana". Al día siguiente, Newton envió un manuscrito con la solución, en latín y anónima, a Montagu, quien era el presidente de la Royal Society, con el encargo de que lo publicara y lo mandara a Bernoulli. Cuentan que cuando Bernoulli recibió el manuscrito anónimo, adivinó de inmediato quién era su autor y exclamó: "¡Al león se le reconoce por la marca de sus garras!". En mayo de 1697, el Acta Eruditorum publicó cuatro soluciones, cuyos autores eran Leibniz, el mismo Bernoulli y su hermano mayor Jacob, y la anónima de Newton. El problema de la braquistocrona y otros semejantes, hicieron que se desarrollara lo que ahora se conoce como calculo de variaciones en mecánica racional o teórica. Un excelente tratamiento de este tema se puede encontrar las pag 40 a 48 en el libro Mecánica Clásica de H Goldstein, libro básico para entender y estudiar los fundamentos de la mecánica. ¿Y cómo se ve una braquistocrona o cicloide? Para darnos una mejor idea coloque un marcador en la periferia de un aro, haga rodar este, sin deslizar, de manera que el marcador marque en una superficie su movimiento, el marcador trazará una cicloide con su parte cóncava hacia abajo. Si este dibujo se da vuelta, obtendrá una braquistocrona. El dibujo tendrá un aspecto como el de la figura, donde el área marcada con 1, no corresponde al dibujo de la cicloide, la forma de esta corresponde a la curva envolvente exterior. 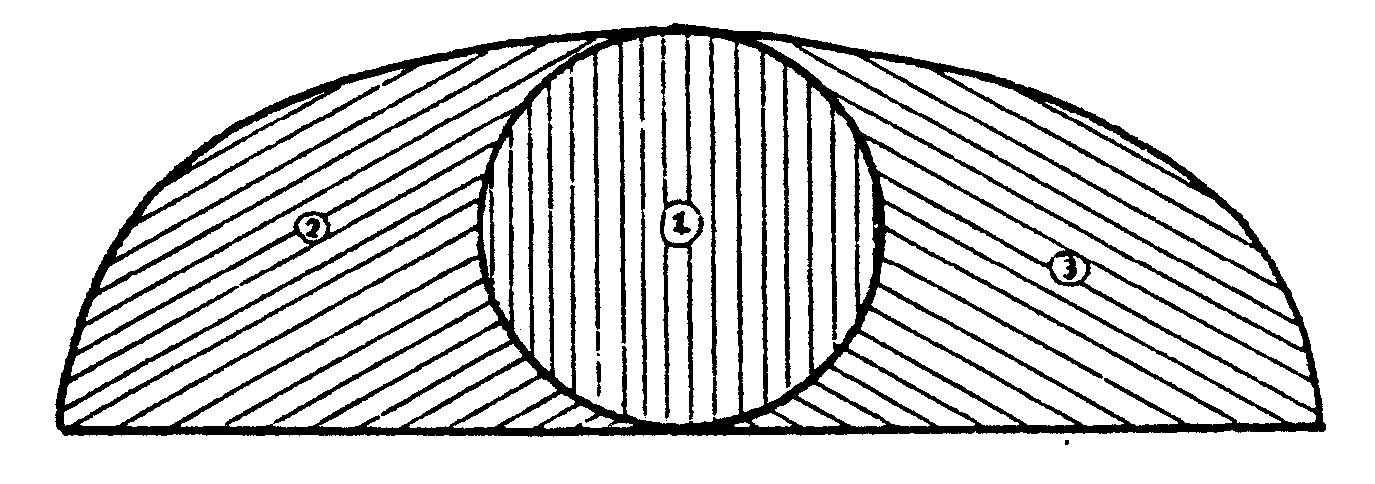 ALGUNAS DEMOSTRACIONES DE PROPIEDADES DE LA BRAQUISTOCRONA Veamos si podemos encontrar la ecuación de la cicloide en forma simple. Tomemos unos ejes coordenados convenientes, sobre la superficie donde se apoya esta rueda y coincidente con la rueda se establecerá el eje x y el eje y será la perpendicular a ella por el punto que se ha señalado en la rueda cuando éste está en el suelo. Si hacemos que la rueda ruede un poco y veamos dónde va a parar el punto P de la circunferencia. Cuando el centro del círculo C ha pasado a C´, el punto P ha pasado a P´. Este es el punto cuya ecuación queremos. Llamamos a sus coordenadas (x,y). Como la rueda no resbala sobre el suelo, lo que sabemos es que la longitud del arco LP sobre la circunferencia es igual a la longitud del segmento rectilíneo OL. Si llamamos a al ángulo LC´P´ medido en radianes, resulta OL=LP´=ra . Por otra parte, las coordenadas de P´en nuestro sistema son: 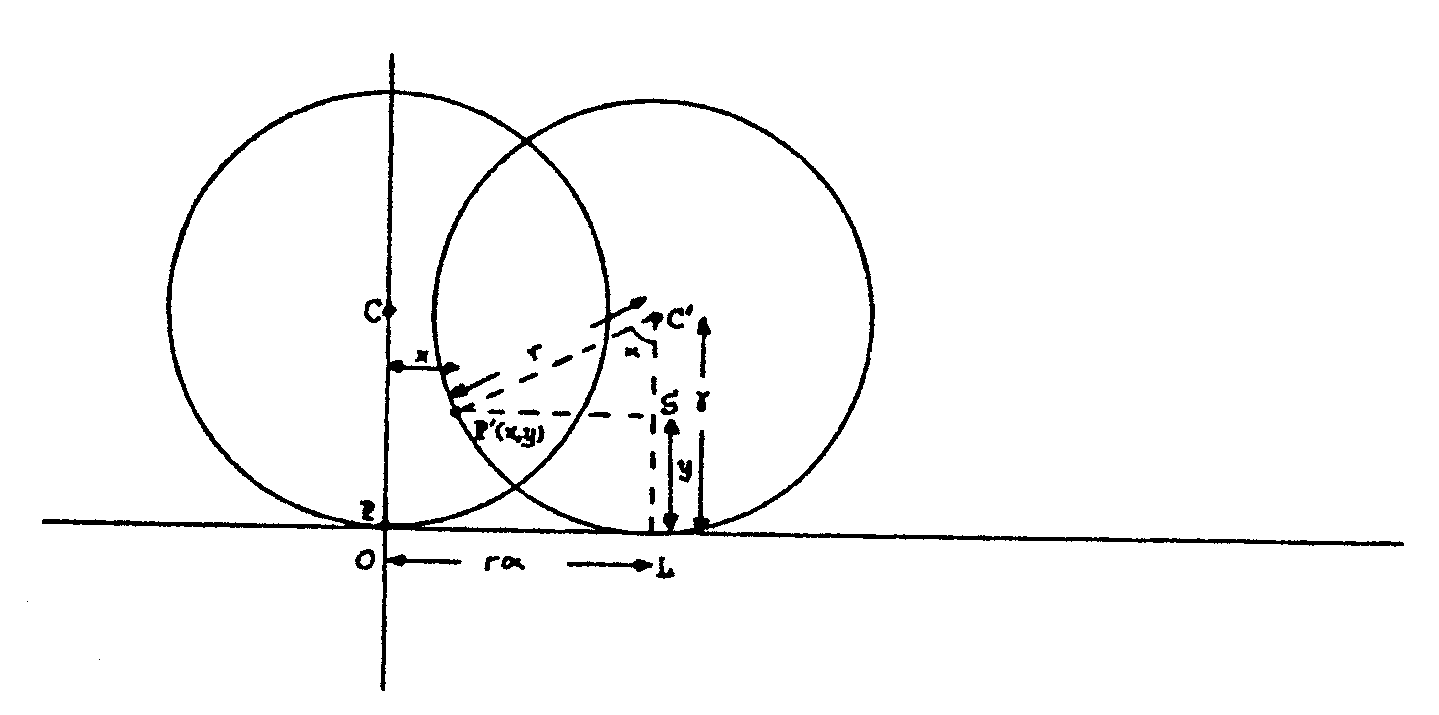 x = OL - P´S = ra - rsena y = SL = C´L - C´S = r - rcosa Así obtenemos la ecuación en coordenadas paramétricas (parámetro a) de la cicloide x = ra - rsena y= r - rcosa Si se intenta eliminar a sale algo más complicado y no lo haremos aquí. La cicloide tiene propiedades geométricas muy interesantes. ¿Cuál será su longitud? La longitud de un segmento ds en el plano x,y es ds=(dx2 +dy2)1/2, la longitud total es la suma de todos los ds, luego dx = r(1-cosa )d a ; dy = rsena . da haciendo uso de la identidad trigonométrica Así resulta que la longitud de la cicloide es 8 veces la del radio de la rueda que la genera. ¿Cuál será el área bajo la cicloide? Se halla de modo sencillo una vez que tenemos la ecuación de la curva 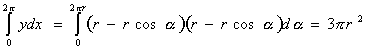 Así el área bajo la cicloide es tres veces la del círculo que engendra la curva. Por tanto las áreas de las tres regiones señaladas en la figura inicial, marcadas con los números 1,2 y 3 son iguales EXPERIENCIAS CON LA BRAQUISTOCRONA El profesor de ciencias debe generar iniciativas de experimentación, ya que este es uno, sino él más importante de los métodos para la enseñanza de las ciencias. Con las ecuaciones parametricas encontradas realizamos a través de algún programa de calculo numérico, en nuestro caso usamos el Excell, para generar una curva que corresponda a una cicloide, cuidando de usar valores de r que permitan generar una curva que este contenida en una hoja común del tipo A4. Otro detalle que debe ser debidamente tenido en cuenta es que la grafica que se genere debe tener la misma escala en ambos ejes, la opción usual e los programas que grafican no tienen esta facilidad. Trasladamos este dibujo a una superficie más firme, en nuestro caso usamos una plancha de telgopor de unos pocos centímetros de espesor, luego cortamos cuidadosamente la curva por su línea, conseguimos así una curva que representa la cicloide en una superficie que podemos trabajar cómodamente. Pegamos una tira de cartulina del borde que representa la curva de la cicloide, de manera que quede una pestaña de aproximadamente de 1 cm en forma perpendicular a la superficie de telgopor. De esta manera una pequeña bolita de virio u otro material puede rodar siguiendo la curva de la cicloide. Con una cartulina más firme, por ejemplo doble, pegamos una tira recta que conforme un plano inclinado recto desde una altura hasta el punto mas bajo de la curva de la cicloide, liberando dos bolitas iguales desde la misma altura una por la cicloide y otra por le tira recta, verificamos que llega primero al punto mas bajo aquella que aparentemente debería llegar mas tarde. Podemos hacer las pruebas cambiando la inclinación de la tira que representa la línea recta. Si reproducimos con un alambre de grosor suficiente como para poder manejarlo cómodamente sin deformaciones, lo usaremos para generar un cuerpo sólido, que represente la cicloide, haciéndolo rotar, previamente calentado, podemos generar sobre un cubo de telgopor, un objeto como el de la figura y hacer experiencia con el. 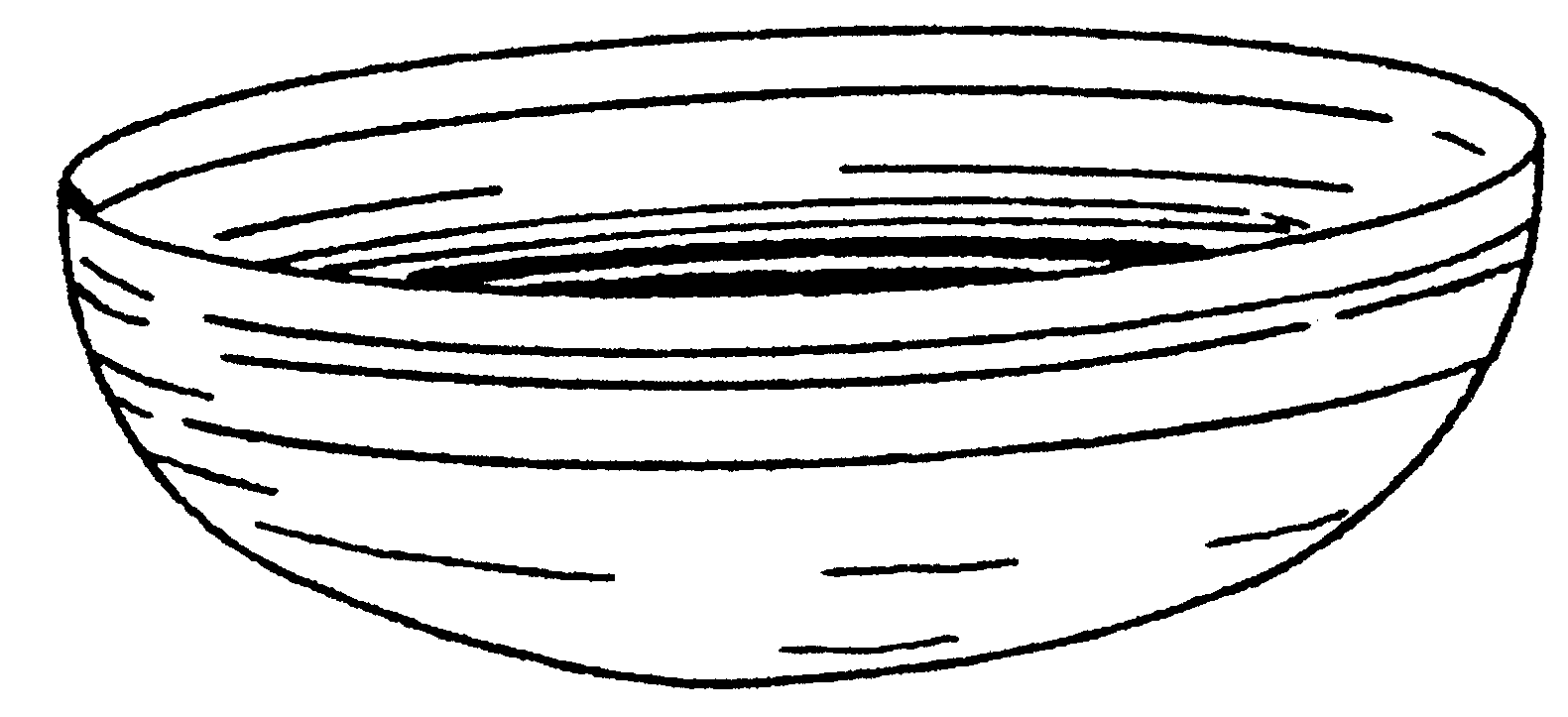 Se puede realizar un orificio del tamaño de las bolitas que se usaron para las experiencias propuestas anteriormente y verificar que dos bolitas, una cayendo por la superficie interior y otra por un plano inclinado, con distintas pendientes, pero ambas liberadas de la misma altura pasará por el orificio central la que se desliza por la curva de la cicliode. Otra experiencia por demás interesante y que indica lo particular de esta geometría es que, si desde dos puntos a altura distinta del cuenco se dejan caer al mismo tiempo dos canicas, resulta que llegan al punto más bajo del cuenco simultáneamente. Esta propiedad que no demostraremos aquí, puede ser verificada experimentalmente.- | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Al Indice | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Llene este formulario con todos los datos posibles, pues nos permitirá generar una base de datos de mucha utilidad para nuestra futura labor.- | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Al Indice | ||||||||||||||||||||||||||||||||||||||||||||||||||||||